ઊભી દીવાલો ધરાવતી ટાંકીમાં $12\, {m}$ ઊંચાઈ સુધી પાણી ભરેલ છે. પાણીના સ્તરથી $'{h}'$ ઊંડાઈએ કોઈ એક દીવાલમાં એક હૉલ કરવામાં આવે છે. બહાર નીકળતી પાણીની ધાર જમીન ઉપર મહત્તમ અવધિ સુધી પહોચે તે માટે $h$ નું મૂલ્ય કેટલું હોવું જોઈએ?
JEE MAIN 2021, Medium
Download our app for free and get started
d
\(R =\sqrt{2 gh } \times \sqrt{\frac{(12- h ) \times 2}{ g }}\)
\(R =\sqrt{2 gh } \times \sqrt{\frac{(12- h ) \times 2}{ g }}\)
\(\sqrt{4 h (12- h )}= R\)
For maximum \(R\)
\(\frac{ d R }{ dh }=0\)
\(\Rightarrow h =6 \;m\)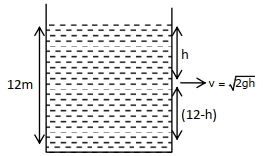
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચેનામાંથી ક્યું આદર્શ (તરલ)નો ગુણધર્મ નથી ?
- 2એક ઊંચી પાણીની ટાંકીનો ઉપરનો ભાગ હવામાં ખુલ્લો છે અને તેનું પાણીનું સ્તર જળવાઈ રહે છે. તેની દિવાલમાં $2\, cm$ ની ત્રિજ્યાના ગોળાકાર કાણામાંથી બહાર $0.74 \,m^3$ પાણી પ્રતિ મિનટ આપે છે. ટાંકીના પાણીના સ્તરથી આ કાણાના કેન્દ્રની ઊંડાઈ _______ $m$ ની નજીકની છે.View Solution
- 3પાણી એ સમક્ષિતિજ જડિત સપાટી પર એવી રીતે વહે છે જેથી પ્રવાહ વેગ $v=K\left(\frac{2 y^2}{a^2} \frac{-y^3}{a^3}\right)$ એ $y$ (લંબવત દિશા) મુજબ બદલાય. જો પાણીનો શ્યાનતા ગુણાંક $\eta$ હોય,તો $y = a$ પર પાણીના $layer$ વચ્ચેનો $Shear\,Stress$View Solution
- 4View Solutionજો ગુરત્વાકર્ષણ ન હોય તો તરલ માટે નીચેનામાંથી ક્યું સત્ય છે ?
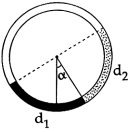
- 5એક વર્તુળાકાર નળી ઊર્ધ્વ સમતલમાં રાખેલ છે.બે પ્રવાહી કે જેઓ એકબીજામાં ભળી શકતા નથી અને તેમની ધનતા $d_1$ અને $d_2$ છે.તેમને આ નળીમાં ભરવામાં આવે છે.દરેક પ્રવાહી કેન્દ્ર આગળ $90°$ નો આંતરિક કોણ રચે છે.જયારે આંતર સપાટીને જોડતી ત્રિજયા શિરોલંબ સાથે $\alpha $ કોણ રચે છે,તો ગુણોત્તર $\frac{{{d_1}}}{{{d_2}}}$View Solution
- 6પાત્રના તળિયે $ l $ લંબાઇ અને $r $ ત્રિજયા ઘરાવતી કેશનળી જોડેલ છે.તેના પર દબાણનો તફાવત $P$ હોય,ત્યારે બહાર આવતા પાણીનું કદ $ V$ છે,હવે તેની સાથે શ્રેણીમાં સમાન લંબાઇ પરંતુ અડધી ત્રિજયા ધરાવતી કેશનળી જોડતાં બહાર આવતાં પ્રવાહીનું કદ કેટલું થાય? ( તંત્ર વચ્ચે દબાણનો તફાવત $P$ છે. )View Solution
- 7View Solutionઆડી પાઈપનો આડછેદનું ક્ષેત્રફળ સમાન નથી, તો પ્રવાહી માટે આ પાઈપમાં નીચેનામાંથી ક્યો સમય બદલાતો નથી?
- 8$w$ જાડાઈ ધરાવતા અને $H$ ઊંંચાઈ ધરાવતા ડેમમાં પાણી ભરવામાં આવે છે, તો ડેમ પર લાગુ પડતું પરીણામી બળ.View Solution
- 9પદાર્થનું વજન હવામાં વજન કરતા પાણીમાં હવામાં વજન કરતાં ત્રીજા ભાગનું છે, તો પદાર્થ ઘનતા ............. $g / cm ^3$View Solution
- 10$900 Kg/m^3$ ઘનતા ધરાવતો બરફનો ટુકડો $1000 Kg/m^3 $ ઘનતા ધરાવતા પાણીમાં તરે છે,બરફનું ....... $\%$ કદ પાણીની બહાર રહે .View Solution