Let the negative charged particle is at \(P\). Thus \(O P=z_0\)
The electric field is at \(P\) due to ring is \(E=\frac{1}{4 \pi \epsilon_0} \frac{Q z_0}{\left(R^2+z_0^2\right)^{3 / 2}}\) where \(Q\) is the charge on the ring.
As the ring is positively charged so \(E\) is always directed away from \(O\).
Hence a negatively charged particle is accelerated towards \(O\) and undergoes periodic motion.
i.e \(m a=-\frac{ q }{4 \pi \epsilon_0} \frac{ Qz _0}{\left( R ^2+ z _0^2\right)^{3 / 2}}\)
For \(z_0 \ll R, m a=-\frac{Q q z_0}{4 \pi \epsilon_0 R^3}\). Thus the acceleration \((a)\) is proportional to the \(z-\) coordinate, and the particle undergoes approximate SHM. As \(E\) is directed always away from \(O\) so when particle \(P\) will cross \(O\), again some attractive force will act on it and hence it will not continue to move along negative \(z\)-axis towards \(z=-\infty\).
Download our appand get started for free
Similar Questions
- 1$\lambda$ વિદ્યુતભાર ઘનતા ધરાવતા બે લાંબા પાતળા વિદ્યુતભારીત સળિયાને એકબીજને સમાંતર $d$ અંતરે મૂકવામાં આવ્યા છે. એક સળીયા બીજા સળીયા પર એકમ લંબાઈ દીઠ લાગતું બળ કેટલું હશે? $\left(\right.$ જ્યાં $\left.k=\frac{1}{4 \pi \varepsilon_0}\right)$View Solution
- 2$R$ ત્રિજ્યા ધરાવતી અર્ધરીંગ પર રેખીય વિદ્યુતભાર ઘનતા $\lambda$ છે,તેના કેન્દ્ર પર $1\, C$ વિદ્યુતભાર મુક્તા તેના પર કેટલું બળ લાગશે?View Solution
- 3સમાન અને વિરૂદ્ધ વિદ્યુતભારની ઘનતા $\sigma$ વાળી બે અને સમાંતર તકતીઓ એકબીજાથી અંતરે આવેલી છે. તકતીઓના વચ્ચે આવેલ બિંદુ આગળ વિદ્યુતક્ષેત્ર ......... છે.View Solution
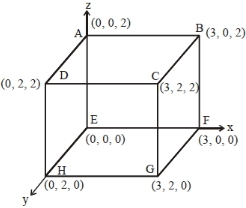
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે બોક્સમાથી $\overrightarrow{\mathrm{E}}=4 \mathrm{x} \hat{\mathrm{i}}-\left(\mathrm{y}^{2}+1\right) \hat{\mathrm{j}}\; \mathrm{N} / \mathrm{C}$ જેટલું વિદ્યુતક્ષેત્ર પસાર થાય છે $A B C D$ અને $BCGF$ સપાટીમાંથી પસાર થતું ફ્લક્સ $\phi_{I}$ અને $\phi_{\mathrm{II}}$ હોય તો તેમનો તફાવત $\phi_{\mathrm{I}}-\phi_{\mathrm{II}}$ ($\mathrm{Nm}^{2} / \mathrm{C}$ માં) કેટલો મળે?View Solution
- 5સમાન અને વિરૂદ્ધ વિદ્યુતભારની ઘનતા $\sigma$ વાળી બે અને સમાંતર તકતીઓ એકબીજાથી અંતરે આવેલી છે. તકતીઓના વચ્ચે આવેલ બિંદુ આગળ વિદ્યુતક્ષેત્ર ......... છે.View Solution
- 6$0.1 \,\mu m$ ત્રિજ્યાનો એક વિદ્યુતભારતીત પાણીનું ટીપુ વિદ્યુતક્ષેત્રની સંતુલન અવસ્થા હેઠળ આવેલ છે. ટીપા પરનો વિદ્યુતભાર ઈલેકટ્રોનીક્સ વિદ્યુતભારને સમતુલ્ય છે. વિદ્યુતક્ષેત્રની તીવ્રતા ........$N/C$ છે.?View Solution
- 7$1$ થી $5$ અંકિત કરેલા પાંચ દડાઓ અલગ-અલગ દોરી વડે લટકાવેલા છે. જોડ $(2, 3)$ અને $(4, 5)$ સ્થિતવિદ્યુત અપાકર્ષણ દર્શાવે છે. જ્યારે જોડ $(1, 2),(3, 5)$ અને $(1, 5)$ સ્થિત વિદ્યુત આકર્ષણ દશાવે છે. $1$ અંકિત દડો કેવો હોવો જોઈએ?View Solution
- 8બે સમાન મૂલ્યના અને વિરુધ્ઘ વિજભારોને અમુક અંતરે મુકતા તેમની વચ્ચે લાગતુ બળ $F$ છે. જો એક વિજભારના $75\%$ વિદ્યુતભાર બીજા વિદ્યુતભારને આપતા તેમની વચ્ચે લાગતુ બળ કેટલું થાય?View Solution
- 9$R$ ત્રિજ્યા ધરાવતી અર્ધરીંગ પર રેખીય વિદ્યુતભાર ઘનતા $\lambda$ છે,તેના કેન્દ્ર પર $1\, C$ વિદ્યુતભાર મુક્તા તેના પર કેટલું બળ લાગશે?View Solution
- 10View Solutionએક ધન વિદ્યુતભારીત લોલક ઉપર તરફના એકરૂપ વિદ્યુતક્ષેત્રમાં દોલન કરે છે. તેનો આવર્તકાળ જ્યારે તે વિદ્યુતક્ષેત્ર વગર દોલન કરે તેની સરખામણીમાં
