$R$ ત્રિજ્યા ધરાવતી અર્ધરીંગ પર રેખીય વિદ્યુતભાર ઘનતા $\lambda$ છે,તેના કેન્દ્ર પર $1\, C$ વિદ્યુતભાર મુક્તા તેના પર કેટલું બળ લાગશે?
AIIMS 2018, Diffcult
c
As, \(R\) be the radius of the ring. Consider a small strip of length \(d l\) having charge \(d q\) lying at an angle \(\theta\).
As, \(R\) be the radius of the ring. Consider a small strip of length \(d l\) having charge \(d q\) lying at an angle \(\theta\).
\(d l=R d \theta\)
Charge on \(d l=\lambda R d \theta\)
Force at \(1 C\) due to \(d l\)
\(=\frac{k \lambda R d \theta}{R^{2}}=\frac{k \lambda}{R} d \theta=d F\)
We need to consider only the component \(d F \cos \theta,\) as the component \(d F \sin \theta\) will cancel out because of the symmetrical element \(d l\).
The total force on \(1 C\) is
\(F=\int_{-\pi / 2}^{\pi / 2} d F \cos \theta\)
\(=\frac{k \lambda}{R} \int_{-\pi / 2}^{\pi / 2} \cos \theta d \theta\)
\(=\frac{k \lambda}{R} \times 2=\frac{2 k \lambda}{R}\)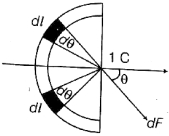
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$1\, g$ જેટલા સમાન દળના બે સમાન ગોળાઓ પરનો સમાન વિદ્યુતભાર $10^{-9}\, C$ છે. જેમને સમાન લંબાઈની દોરીઓ વડે મુક્ત કરવામાં આવે છે. જો ગોળાનો કેન્દ્રો વચ્ચેનું અંતર $0.3\, cm$ હોય તો દોરીના પ્રક્ષેપણ કોણ શિરોલંબ ઘટક સાથે ...... હશે.View Solution
- 2View Solutionએક હવા ભરેલા વિદ્યુતભારીત સુવર્ણ પત્રક વિદ્યુત દર્શકમાં તેના પત્રો ચોક્કસ અંતરે દૂર છે. જ્યારે વિદ્યુત દર્શક પર ક્ષ-કિરણો આયાત કરવામાં આવે તો પત્રો
- 3View Solutionદ્વિ ધ્રુવીય ચાકમાત્રાનો એકમ ......... છે.
- 4$ + \lambda \,C/m$ અને $ - \lambda \,C/m$ના બે સમાંતર અનંત રેખીય વિધુતભારો કે જે રેખીય વિજભાર ઘનતા ધરાવે છે તેઓને મુક્ત અવકાશમાં એક બીજાથી $2R$ અંતરે મુકેલ છે. આ બે રેખીય વિજભારની મધ્યમાં વિદ્યુતક્ષેત્ર કેટલું હશે ?View Solution
- 5$+7\ \mu C$ અને $-5\ \mu C$ વિદ્યુતભાર ધરાવતા બે બોલ એકબીજાને $F$ બળ સાથે આકર્ષે છે. જો બંનેમાં $-2\ \mu C$ વિદ્યુતભાર ઉમેરવામાં આવે તો તેમની વચ્ચેનું બળ કેટલું હશે ?View Solution
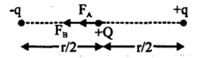
- 6આપેલ આકૃતિમાં $'O'$ એ $AB$ નું મધ્યબિંદુ હોય તો $Q$ વિદ્યુતભાર પરનું બળ ગણો.View Solution
- 7બે બિંદુવત વિદ્યુતભારો $q_2$ = $3 \times 10^{-6}\ C$ અને $q_1$ =$ 5 \times 10^{-6}\ C$ એ $B \,(3, 5, 1)\ m $ આગળ અને $A\, (1, 3, 2)\ m$ આવેલા છે. $q_2$ ના લીધે $q_1$ પર બળનું મૂલ્ય શોધો.View Solution
- 8ડાઈપોલ માટે $q = 2 × 10^{-6}\ C ; d = 0.01\ m$ જો $E = 5 ×10^{5}\ N/C $ હોય તો ડાઈપોલ પર લાગતું મહત્તમ ટોર્ક શોધો.View Solution
- 9હવામાં $r$ અંતરે રહેલા બે વિદ્યુતભાર પર લાગતું બળ $F$ છે.હવે $k$ ડાઇઇલેકિટ્રક ધરાવતા માધ્યમમાં કેટલા અંતરે મૂકવાથી તેમના પર લાગતું બળ સમાન થાય?View Solution
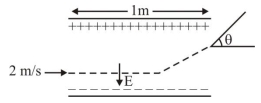
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે $1\,m$ ની પ્લેટોની લંબાઈ વાળી બે સમાંતર પ્લેટો વચ્ચે $E =(8 m / e ) V / m$ જેટલું નિયમિત વિદ્યુતક્ષેત્ર ઉત્પન્ન કરવામાં આવે છે. (જ્યાં $m =$ ઈલેકટ્રોનનું દળ, અને $e =$ ઈલેકટ્રોનનો વિદ્યુતભાર છે). એક ઈલેકટ્રોન પ્લેટોની વચ્ચે સંમિત રીતે $2\,m / s$ ની ઝડપથી દાખલ થાય છે. જ્યારે તે ક્ષેત્રની બહાર નીકળે ત્યારે ઈલેકટ્રોનના પથનું વિચલન $..............$ હશે.View Solution