ઉપરોક્ત પ્રક્રિયામાં $o/p$ ગુણોત્તર સૌથી વધુ હશે ત્યારે..
Diffcult
Download our app for free and get started
a
$(a)$ The steric demand of $H^{\ominus}$ is, however extremely small, and when attack on $C_6H_5Y$ is by any other electrophile, $E^{\oplus}$ , which will necessarily be larger, there will be increasing interaction between $E$ and $Y$ in the transition state for attack at the position $o-$ to $Y (57 \,b, R = E)$ as attacking electrophile and substituent increase in size ; there can be no such interaction in the transition state for $p-$ attack $(57a, R = E)$. This will be reflected in an increasing $\Delta \,G^+$ for $o-$ attack, a consequently slower reaction, and the relative proportion of $o-$ product will thus fall as the size of $E$ and / or $Y$ increase. This is illustrated by the falling $f_{o^-} /f_{p^-}$ ratios which are observed for the nitration of alkylbenzenes $(Y ---CH_3 \to CMe_3)$ under comparable conditions ;
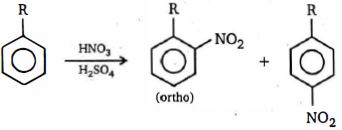
$(a)$ The steric demand of $H^{\ominus}$ is, however extremely small, and when attack on $C_6H_5Y$ is by any other electrophile, $E^{\oplus}$ , which will necessarily be larger, there will be increasing interaction between $E$ and $Y$ in the transition state for attack at the position $o-$ to $Y (57 \,b, R = E)$ as attacking electrophile and substituent increase in size ; there can be no such interaction in the transition state for $p-$ attack $(57a, R = E)$. This will be reflected in an increasing $\Delta \,G^+$ for $o-$ attack, a consequently slower reaction, and the relative proportion of $o-$ product will thus fall as the size of $E$ and / or $Y$ increase. This is illustrated by the falling $f_{o^-} /f_{p^-}$ ratios which are observed for the nitration of alkylbenzenes $(Y ---CH_3 \to CMe_3)$ under comparable conditions ;
Increase in size of $Y$ $\begin{gathered}
\downarrow \hfill \\
\downarrow \hfill \\
\downarrow \hfill \\
\downarrow \hfill \\
\downarrow \hfill \\
\end{gathered} $ $\begin{array}{*{20}{c}}
Y&{\% \,\,o - }&{\% \,p\, - } \\
{C{H_3}}&{58}&{37} \\
{C{H_2}Me}&{45}&{49} \\
{CHM{e_2}}&{30}&{62} \\
{CM{e_3}}&{16}&{73}
\end{array}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ફ્રિડલ ક્રાફટસ પ્રક્રિયામાં નિર્જળ $AlCl_3$ નું કાર્ય ........ છે.View Solution
- 2નીચેની પ્રક્રિયાઓના ક્રમમાં એક જ સમતલમાં $'C$'માં અણુઓની મહત્તમ સંખ્યા હાજર છેView Solution
$A \xrightarrow[ { Cu\; tube }]{\text { Redhot }}\mathrm{B} \xrightarrow[ Anhydrous AlCl_3]{\mathrm{CH}_{3} \mathrm{Cl}(1 \mathrm{eq}} \mathrm{C}$
($A$ એ સૌથી ઓછું પરમાણ્વીય વજન ધરાવતું આલ્કાઇન છે)
- 3View Solutionનીચેનામાંથી કઈ પ્રક્રિયામાં, માર્કોવનિકોફના નિયમનું ઉલ્લંઘન થાય છે?
- 4$\begin{array}{*{20}{c}}View Solution
{M{e_2}CH - CH - Me} \\
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\,\,\,\,\,\,\,\,\,\,} \\
{\,\,\,\,\,\,\,\,OH}
\end{array}\xrightarrow[{350{\,^o}C}]{{A{l_2}{O_3}}}(A)\xrightarrow[{(ii)\,AgOH}]{{(i)\,HI}}(B)$ઉપરોક્ત પ્રકિયા માં નીપજ $(B)$ શું હશે ?
- 5$Br_2$ થી ટ્રાન્સ- $2$ -બ્યુટીન માં ઉમેરવું એક ઉત્પાદન આપે છે જે કયું છે ?View Solution
- 6View Solutionફ્રિડલ-ક્રાફટ્સ પ્રક્રિયામાં ટોલ્યુઇન...... વડે બનાવી શકાય.
- 7View Solutionએરોમેટિક સંયોજનોના નાઈટ્રેશન પર નીચેના વિધાનોમાં કયુ ખોટું છે?
- 8નીચે બતાવેલ $3,3$ - ડાયમિથાઇલ - $1$ -બ્યુટીન ના વધારાને ધ્યાનમાં લો.નિરીક્ષણ કરેલ નીપજ ની રચના માટે શ્રેષ્ઠ પદ્ધતિઓની સમજૂતી શું છે?View Solution
- 9View Solutionકઇ પ્રક્રિયામાં આલ્કેન અને આલ્કીન બંને મળે છે ?
- 10નીચેની પ્રક્રિયામાં $M$ અને $R$ અનુક્રમે ........ હશે.View Solution
$C{H_2} = C{H_2}\xrightarrow[{oxid}]{{Hypochloro}}$ $M\xrightarrow{R}\begin{array}{*{20}{c}}
{C{H_2} - OH} \\
{|\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\
{C{H_2} - OH}
\end{array}$