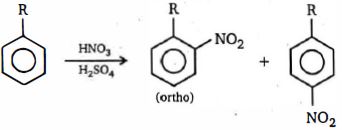
ઉપરોક્ત પ્રક્રિયામાં $o/p$ ગુણોત્તર સૌથી વધુ હશે ત્યારે..

Diffcult
a
\((a)\) The steric demand of \(H^{\ominus}\) is, however extremely small, and when attack on \(C_6H_5Y\) is by any other electrophile, \(E^{\oplus}\) , which will necessarily be larger, there will be increasing interaction between \(E\) and \(Y\) in the transition state for attack at the position \(o-\) to \(Y (57 \,b, R = E)\) as attacking electrophile and substituent increase in size ; there can be no such interaction in the transition state for \(p-\) attack \((57a, R = E)\). This will be reflected in an increasing \(\Delta \,G^+\) for \(o-\) attack, a consequently slower reaction, and the relative proportion of \(o-\) product will thus fall as the size of \(E\) and / or \(Y\) increase. This is illustrated by the falling \(f_{o^-} /f_{p^-}\) ratios which are observed for the nitration of alkylbenzenes \((Y ---CH_3 \to CMe_3)\) under comparable conditions ;
\((a)\) The steric demand of \(H^{\ominus}\) is, however extremely small, and when attack on \(C_6H_5Y\) is by any other electrophile, \(E^{\oplus}\) , which will necessarily be larger, there will be increasing interaction between \(E\) and \(Y\) in the transition state for attack at the position \(o-\) to \(Y (57 \,b, R = E)\) as attacking electrophile and substituent increase in size ; there can be no such interaction in the transition state for \(p-\) attack \((57a, R = E)\). This will be reflected in an increasing \(\Delta \,G^+\) for \(o-\) attack, a consequently slower reaction, and the relative proportion of \(o-\) product will thus fall as the size of \(E\) and / or \(Y\) increase. This is illustrated by the falling \(f_{o^-} /f_{p^-}\) ratios which are observed for the nitration of alkylbenzenes \((Y ---CH_3 \to CMe_3)\) under comparable conditions ;
Increase in size of \(Y\) \(\begin{gathered}
\downarrow \hfill \\
\downarrow \hfill \\
\downarrow \hfill \\
\downarrow \hfill \\
\downarrow \hfill \\
\end{gathered} \) \(\begin{array}{*{20}{c}}
Y&{\% \,\,o - }&{\% \,p\, - } \\
{C{H_3}}&{58}&{37} \\
{C{H_2}Me}&{45}&{49} \\
{CHM{e_2}}&{30}&{62} \\
{CM{e_3}}&{16}&{73}
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસોડિયમ કાર્બોનેટના જલીય દ્રાવણે પ્રત્યે નીચેના પૈકી ક્યુ સંયોજન સૌથી વધુ પ્રતિક્રિયાત્મક છે ?
- 2View Solutionકયો અણુ દ્વિ - ધ્રુવ ચાકમાત્રા ધરાવે છે ?
- 3કઈ પ્રતિક્રિયામાં સૌથી ઓછુ $\Delta {{G}^{\begin{smallmatrix}View Solution
+ \\
+
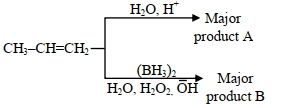
\end{smallmatrix}}}$ અથવા (સક્રિયકરણ ઉર્જા) - 4નીચે આપેલ પ્રક્રિયાઓના સેટ માં નીપજ $\mathrm{A}$ અને નીપજ $\mathrm{B}$ ઓળખો :View Solution
- 5$C_6H_{12}$ સંયોજન...... છે.View Solution
- 6View Solutionવિવિધ સાયક્લોઆલકેન્સ અને કાર્બોકેટાયનની સ્થિરતા, તેમજ કાર્બોકેટાયનની ફરીથી ગોઠવવાની પદ્ધતિઓનું સંચાલન કરતા નિયમો ધ્યાનમાં લઈ.આ પ્રક્રિયાનું સૌથી સંભવિત નીપજ શું છે?
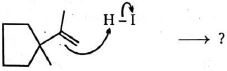
- 7View Solutionનીચેની પ્રક્રિયામાં ક્યો ઉદ્દીપક વપરાય છે ?

- 8View Solutionશેમાં મહત્તમ કાર્બન-કાર્બન બંધ-અંતર જોવા મળે છે?
- 9નીચેની પ્રક્રિયાની નિપજો કઈ છે ?View Solution
$C{H_3}C \equiv \,C\,C{H_2}C{H_3}\mathop {\xrightarrow[{(2)\;Hydrolysis}]{}}\limits^{(1)\;\;{O_3}} $ .......
- 10આલ્કીન $R - C - H = C{H_2}$ ની ${B_2}{H_{6}}$ સાથેની પ્રક્રિયાથી નીપજ $B$ મળે છે, જેનું આલ્કલાઇન હાઇડ્રોજન પેરોક્સાઇડ વડે ઓક્સિડેશન શુ ઉત્પન્ન કરશે ?View Solution
