વધારે સંખ્યામાં એકસમાન બિંદુુવત્ દળો $m$ ને $x$-અક્ષ પર, $x=0,1,2,4, \ldots \ldots$. મૂકવામાં આવેલા છે. તો ઊગમબિંદુ $(x=0)$ પર રહેલા $m$ દળ પરનું ગુરુત્વાકર્ષણ બળનું મૂલ્ય શું હશે ?
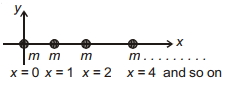
Medium
b
(b)
(b)
Let, \(F_1, F_2, F_4, F_8 \ldots \ldots\) be the forces of gravitation due masses ' \(m\) ' at \(x=1,2,4,8 \ldots\) respectively.
\(\Rightarrow F_1=\frac{G m^2}{1^2}\)
\(F_2=\frac{G m^2}{2^2}\)
\(F_4=\frac{G m^2}{4^2}\)
\(F_8 =\frac{G m^2}{8^2}\)
\(F_1+F_2+F_4+F_8 \ldots=G m^2\left(\frac{1}{1}+\frac{1}{4}+\frac{1}{16}+\frac{1}{64} \ldots\right)\)
infinite \(G.P\). with common ratio \(=\frac{1}{4}\)
For an infinite \(G.P\), sum \(=\left(\frac{a}{1-r}\right)\)
\(a\) is the first term
\(r\) is the common ratio
\(\Rightarrow \text { Sum }=\frac{1}{1-\frac{1}{4}}=\left(\frac{4}{3}\right)\)
\(\Rightarrow F_1+F_2+F_4+F_8 \ldots \ldots=\frac{4}{3} G m^2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$g, R$ અને $G$ ના પદમાં પૃથ્વીના દળનું સૂત્ર શું થાય?View Solution
- 2પૃથ્વીની સપાટીથી $1\; km$ ઊંચાઇએ ગુરુત્વપ્રવેગ પૃથ્વીની સપાટીથી $d$ ઊંડાઇએ ગુરુત્વપ્રવેગ જેટલો છે, તો ઊંડાઈ $d\,=$ ......... $km$View Solution
- 3પૃથ્વીની આસપાસ વર્તુળાકાર કક્ષામાં ઉપગ્રહ અચળ ઝડપ $v$ થી ભ્રમણ કરે છે.જો પૃથ્વીનું ગુરુત્વાકર્ષણ લાગતું બંધ થઇ જાય તોView Solution
- 4એક ગ્રહને ફરતે સ્થિર કક્ષામાં ભ્રમણ કરતા એક સેટેલાઈટ (ઉપગ્રહ)નો આવર્તકાળ $6$ કલાક છે. ગ્રહનું દળ પૃથ્વીના દળ કરતાં ચોથા ભાગનું છે. ગ્રહની કક્ષાની ત્રિજ્યાં. . . . . . . હશે.View Solution
(પૃથ્વી માટે ભૂસ્તરીય કક્ષાની ત્રિજ્યાં $4.2 \times 10^4 \mathrm{~km}$ આપેલ છે.)
- 5જો પૃથ્વી $R$ ત્રિજ્યાનો ગોળો હોય અને $g_{30}$ એ $30^o $ અક્ષાંશ પર ગુરુત્વ પ્રવેગ અને $g $ એ વિષુવવૃત પરનો પ્રવેગ તો $g - g_{30}$ નું મૂલ્ય કેટલું થાય?View Solution
- 6View Solutionબે ગ્રહો સમાન ધનતાં પરંતુ જુદી જુદી ત્રિજ્યો ધરાવે છે તો ગુરુત્વપ્રવેગ એ ....
- 7જે પૃથ્વીના દળમાં $25 \%$ જેટલો ઘટાડો થાય અને તેની ત્રિજ્યામાં $50 \%$ જેટલો વધારો થાય, તો તેની સપાટી પર ગુરુત્વપ્રવેગમાં અંદાજે કેટલો ઘટાડો ($\%$) થશે ?View Solution
- 8$m $ દળના બે કણો પરસ્પરના ગુરુત્વાકર્ષણ બળની અસર હેઠળ $R $ ત્રિજયાના વર્તુળ પર ગતિ કરે છે. કોઇ એક કણની આ કણોના બનેલા તંત્રના દ્રવ્યમાન કેન્દ્રની સાપેક્ષે ઝડપ કેટલી હશે?View Solution
- 9એક પૃથ્વીનો ઉપગ્રહ $'x'$ પૃથ્વીની કક્ષામાં ભ્રમણ કરી રહ્યો છે. જેની ત્રિજ્યાએ કમ્યુનીકેશન ઉપગ્રહની કક્ષાની ત્રિજ્યા કરતાં $1 / 4$ ભાગ જેટલી છે. તો $X$ ના પરિભ્રમણનો આવર્તકાળ ......... હશે?View Solution
- 10બે ગ્રહ જેની ત્રિજ્યાનો ગુણોત્તર $K$ પરંતુ ગુરુત્વપ્રવેગ નો ગુણોત્તર $g$ છે.તો તેમની નિષ્ક્રમણ ઝડપ નો ગુણોત્તર કેટલો થાય?View Solution
