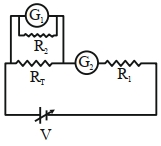
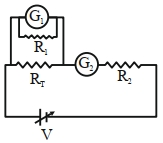
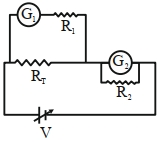
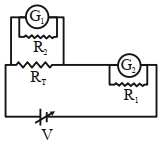
વિદ્યાર્થીને ચલિત વોલ્ટેજ સ્ત્રોત $V$, પરીક્ષણ અવરોધ $R_T=10\,\Omega$, બે સરખા ગેલ્વેનોમીટર $G_1$ અને $G_2$ અને બે વધારાના અવરોધ, $R _1=10\,M\Omega$ અને $R _2=0.001\,\Omega$ આપવામાં આવે છે.ઓહ્મના નિયમને ચકાસવા માટેનો પ્રયોગ કરવા માટે, સૌથી યોગ્ય પરિપથ કયો છે?
- A
- B
- C
- D
JEE MAIN 2023, Medium
Download our app for free and get started
c
To convert galvanometer into ammeter low resistances should be added into parallel and for voltmeter conversion, a very high resistance should be added in series.
To convert galvanometer into ammeter low resistances should be added into parallel and for voltmeter conversion, a very high resistance should be added in series.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક મીટર બ્રીજના પ્રયોગમાં ગેપમાં $2\,\Omega$ અને $3\,\Omega$ મૂકવામાં આવે તો સંતુલનબિંદુ મળે છે. સંતુલન બિંદુને $22.5\,cm$ સ્થાનાંતરિત કરવા માટે $3\,\Omega$ અવરોધ સાથે $X\,\Omega$ નો શંટ જોડવામાં આવે છે.તો $X$ નું મૂલ્ય $...........$ છે.View Solution
- 2$200\, {W},\;100 \,{V}$ ના રેટિંગ ધરાવતા બલ્બને $200\, {V}$ ના ઉદગમ સાથે જોડેલ છે. કેટલા મૂલ્યના ($\Omega$ માં) $R$ અવરોધને તેની સાથે શ્રેણીમાં જોડાવો જોઈએ કે જેથી બલ્બ સમાન પાવર આપે?View Solution
- 3તાંબામાં મુક્ત ઇલેકટ્રોનની સંખ્યા ઘનતા લગભગ $8 \times 10^{28}\,m ^{-3}$ જેટલી છે. તાંબાના તારના આડછેદનું ક્ષેત્રફળ $= 2 10^{-6}\,m ^2$ છે અને તે $3.2\,A$ પ્રવાહનું વહન કરે છે. ઇલેકટ્રોનની ડ્રીફટ ઝડપ $.......\times 10^{-6}\,ms ^{-1}$ છે.View Solution
- 4જો $\sigma_1$, $\sigma_2$ અને $\sigma_3$ ત્રણ વાહકોની વાહકતા હોય તો જ્યારે તેઓને શ્રેણીમાં જોડવામાં આવે તો તેની સમતુલ્ય વાહકતા .......હશે.View Solution
- 5મીટર બ્રીજના પ્રયોગમાં તટસ્થ બિંદુ વાયરના એક છેડેથી $20\, cm$ એ મળે છે. જ્યારે અવરોધ $X$ બીજ અવરોધ $y$ સાથે સંતુલન થયેલ છે. જો $x < y$, હોય તો $4X$ અવરોધને $Y$ અવરોધ સાથે સંતુલન કરવા નવા તટસ્થ બિંદુનું તે જ બિંદુથી અંતર............ $cm$ હશે.View Solution
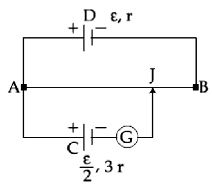
- 6$L$ લંબાઇનો અને $12\, r$ નો અવરોધ ધરાવતા એક પોટેન્શીયોમીટર તાર $AB$ અને $\varepsilon$ જેટલું $emf$ અને $r$ જેટલો આંતરિક અવરોધ ધરાવતા કોષ $D$ સાથે જોડવામાં આવે છે. $\varepsilon/2$ જેટલું $emf$ અને $3r$ જેટલો આતંરિક અવરોધ ધરાવતા કોષ $C$ ને આકૃતિમાં દર્શાવ્યા મુજબ જોડવામાં આવે છે. ગેલ્વેનોમીટરમાં દર્શાવતું શૂન્ય આવર્તન માટેની લંબાઈ $AJ$ _______ હશે.View Solution
- 7.............. $^oC$ તાપમાને કોપર વાયરનો અવરોધ તેના $0\,^oC$ તાપમાને અવરોધ કરતા $3$ ગણો થશે ? (અવરોધકતાનો તાપમાન ગુણાંક $= 4 = 10^{-3}\, C$)View Solution
- 8$4 \times 10^{-6}\;m^{2}$ આડછેદ ધરાવતા તારમાંથી $10\, amp$ પ્રવાહ વહે છે.એલ્યુમિનિયમની ઘનતા $2.7\, gm / cc$ છે. એલ્યુમિનિયમ એક પરમાણુ દીઠ એક ઇલેક્ટ્રોન વહનમાં આપે છે.જો એલ્યુમિનિયમનો અણૂભાર $27$ ગ્રામ હોય તો ઇલેક્ટ્રોનનો ડ્રિફ્ટવેગ ......... $\times 10^{-4} \,m / s$ થાય.View Solution
- 9$R$ અવરોધ અને ત્રિજ્યા $r$ ધરાવતતા એક તારને ત્યાં સુધી ખૅંયવામાં આવ છે કે જ્યાં સુધી ત્રિજ્યા $(r / 2)$ થાય. જો ખેયાયેલા તારનો નવો અવરોધ $x R$ છે. તો $x=$ . . . . . થશે.View Solution
- 10જ્યારે કળ બંધ કરવામાં આવે ત્યારે બેટરીમાંથી બહાર આવતો પ્રવાહ ....... ($A$ માં)View Solution
