$x-$ અક્ષ પર કણનું સ્થાનાંતર $x = a\sin^2 \omega t$ દ્વારા આપવામાં આવે છે. આ કણની ગતિ કોને અનુરૂપ થાય?
AIPMT 2010, Medium
c
\(x=a \sin ^{2} \omega t=a\left(\frac{1-\cos 2 \omega t}{2}\right)\)
\(x=a \sin ^{2} \omega t=a\left(\frac{1-\cos 2 \omega t}{2}\right)\)
\(\left(\because \cos 2 \theta=1-2 \sin ^{2} \theta\right) \)
\(= \frac{a}{2}-\frac{a \cos 2 \omega t}{2}\)
\(\therefore \quad\) Velocity, \(v=\frac{d x}{d t}=\frac{2 \omega a \sin 2 \omega t}{2}=\omega a \sin 2 \omega t\)
Acceleration, \(a=\frac{d v}{d t}=2 \omega^{2} a \cos 2 \omega t\)
For the given displacement \(x=a \sin ^{2} \omega t,\)
\(a \propto-x\) is not satisfied.
Hence, the motion of the particle is non simple harmonic motion.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જયારે સ્પ્રિંગ સાથે $M$ દળ લગાવીને સરળ આવર્તગતિ કરાવવામાં આવે છે.ત્યારે આવર્તકાળ $T$ છે.જયારે દળમાં $m$ નો વઘારો કરવામાં આવે છે.ત્યારે આવર્તકાળ $ \frac{{5T}}{4} $ છે.તો $ \frac{m}{M} $ =_______View Solution
- 2View Solutionબાજુની આકૃતિમાં દર્શાવ્યા મુજબ, જો કોઈ લીસા ઢાળ પર સરખી સ્પ્રિંગોથી કોઈ દળ ગોઠવેલું હોય તો આ દોલન કરતા તંત્રનો આવર્તકાળ કેટલો થશે ?
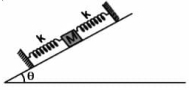
- 3View Solutionસરળ આવર્ત ગતિ કરતાં એક કણના સ્થાનાંતર અને પ્રવેગ વચ્ચેનો કળા તફાવત .......... છે
- 4જયારે બ્લોકને $2x_0$ દબાવીને મૂકત કરતા બ્લોકને દિવાલ સાથે અથડાતા કેટલો સમય લાગશે?View Solution
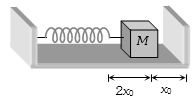
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણે એક રિંગને $S$ બિંદુથી જડિત કરેલ છે.જયારે તેને સંતુલનથી સ્થાનતરિત કરવામાં આવે ત્યારે તે $1\,second$ ના આવર્તકાળથી ડોળાનો કરે છે.તો રીંગની ત્રિજ્યા $m$ માં કેટલી હશે?View Solution
($g = \pi ^2$ )
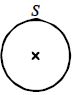
- 6View Solutionનીચેનામાંથી કઈ દોલિત ગતિ છે?
- 7સમતોલન સ્થાન પાસેથી સરળ આવર્ત ગતિ શરૂ કરતાં પદાર્થનો કંપવિસ્તાર $a $ અને આવર્તકાળ $3\, sec$ છે.સમતોલન બિંદુથી અડધા કંપવિસ્તાર સુધી પહોંચવા માટે કેટલો સમય ..... $\sec$ લાગે?View Solution
- 8$10\, N$ ના બળ દ્વારા એક સ્પ્રિંગને $5\, cm$ જેટલી ખેંચવામાં આવે છે. જ્યારે $2\, kg$ નું દળ લટકાવવામાં આવે તો દોલનોનો આવર્તકાળ $.....\,s$ છે.View Solution
- 9સરળ આવર્ત ગતિ કરતાં પદાર્થનો કંપવિસ્તાર $3\, cm$ અને આવર્તકાળ $6 \,second$ છે.તો સમતોલ સ્થાન પાસે વેગ($cm/sec$ માં) કેટલો થાય?View Solution
- 10સરળ આવર્ત ગતિ કરતાં પદાર્થનો કંપવિસ્તાર $4\,cm$ છે,સમતોલન સ્થાનથી કેટલા અંતરે ગતિઊર્જા અને સ્થિતિઊર્જા સમાન થાય?View Solution
