\(= 2 \times10^{-3}m, D = 2 m, \lambda _1 = 12000 \times 10^{-10} m,\lambda_ 2= 10000 \times10^{-10}\, m\)
અહીં, બંને તરંગલંબાઈવાળા પ્રકાશની પ્રકાશિત શલાકાઓ એકબીજા પર સંપાત થાય છે. તેથી બંને માટે
\(\frac{{{\text{xd}}}}{{\text{D}}}\,\, = \,\,{{\text{n}}_{\text{1}}}\lambda {l_2}\)અને \(\frac{{{\text{xd}}}}{{\text{D}}}\,\, = \,\,{{\text{n}}_{\text{2}}}{\lambda _{\text{2}}}\) પર થી \(,\,\,{{\text{n}}_{\text{1}}}{\lambda _{\text{2}}}\,\, = \,\,{{\text{n}}_{\text{2}}}{\lambda _{\text{2}}}\)થાય
\(\therefore \,\,\frac{{{n_1}}}{{{n_2}}}\,\, = \,\,\frac{{{\lambda _2}}}{{{\lambda _1}}}\,\, = \,\,\frac{{10000}}{{12000}}\,\, = \,\,\frac{5}{6}\)
તેથી \(n_1\) નું લઘુતમ મૂલ્ય \(5\)અને \(n_2\) નું લઘુતમ મૂલ્ય\(6\) છે.
હવે,\(\frac{{xd}}{D}\,\, = \,\,{n_1}{\lambda _1}\,\,\,\,\therefore \,\,\,\,x\,\, = \,\,\frac{{{n_1}{\lambda _1}D}}{d}\,\)
\( = \,\,\frac{{5\,\,\, \times \,\,12000\,\, \times \,\,{{10}^{ - 10}}\, \times \,\,2}}{{2\,\, \times \,\,{{10}^{ - 3}}}}\,\, = \,\,6\,\, \times \,\,{10^{ - 3}}\,m\,\, = \,\,6\,\,mm\)
Download our appand get started for free
Similar Questions
- 1યંગના ડબલ સ્લિટના પ્રયોગમાં $5890 Å $ તરંગલંબાઇ માટે શલાકાની કોણીય પહોળાઇ $0.20^o$ છે.હવે,પ્રયોગ પાણીમાં કરતાં શલાકાની કોણીય પહોળાઇ કેટલા .....$^o$ થાય?View Solution
- 2યંગ ડબલ સ્લિટના પ્રયોગમાં $450 \,nm$ તરંગલંબાઈ માટે, $2 \,m$ દૂર રખેલા પડદા ઉપર શલાકાની પહોળાઈ $0.35^{\circ}$ જેટલી મળે છે. આ આખીય રચનાને $7 / 5$ જેટલો વક્રીભવનાંક ધરાવતા માધ્યમમાં ડૂબાડવામાં આવે તો શલાકાની કોણીય પહોળાઈ $\frac{1}{\alpha}$ થાય છે. તો $\alpha$ નું મૂલ્ય ............ હશે.View Solution
- 3યંગના પ્રયોગમાં પડદા પરના જે બિંદુએ પથ-તફાવત $\lambda/6$ છે ત્યાં તીવ્રતા $I$ છે. જો મધ્યસ્થ પ્રકાશિત શલાકાની તીવ્રતા $I_0$ હોય, તો $I/I_0$ = …View Solution
- 4$650\, nm$ અને $655\,nm$ તરંગલંબાઈ ધરાવતી સોડીયમ પ્રકાશનો ઉપયોગ $0.5\, mm$ પહોળાઈ ધરાવતી સિંગલ-સ્લિટ દ્વારા મળતા વિવર્તનનો અભ્યાસ કરવામાં થાય છે. સ્લિટ અને પડદા વચ્ચે નું અંતર $2.0\, m$ છે. આ બંને કિસ્સામાં મળતી વિવર્તન ભાતમાં પ્રથમ મહત્તમો વરચેનું અંતર......... $\times 10^{-5} m$ હશે.View Solution
- 5માઈક્રોસ્કોપના ઓબ્જેક્ટિવ લેન્સ માટેના ન્યૂમેરિકલ અપેચર (numerical aperature) નું મૂલ્ય $1.25$ છે.પ્રકાશની તરંગલંબાઈ $5000\,\mathop A\limits^o $ હોય તો બે બિંદુ વચ્ચેનું ન્યુનત્તમ અંતર કેટલું હોવું જોઈએ જેથી તેમણે અલગ અલગ રીતે પારખી શકાય.....$\mu m$ (સ્પષ્ટ રીતે જોઇ શકાય) ?View Solution
- 6View Solutionપાણી ની સપાટી પર તરતા તેલના ટીપાના રંગો વ્યતિકરણના કારણે દેખાય છે. તો તરતા તેલના ટીપાની જાડાઈ ક્યા ક્રમમાં હોવી જોઈએ?
- 7એકક $590\; nm$ તરંગ લંબાઈવાળો અને બીજ અજ્ઞાત મૂલ્યની તરંગલંબાઈવાળા પ્રકાશનું મિશ્રણ યંગની ડબલ સ્લિટને પ્રકાશિત કરે છે. તેના કારણે પડદા પર બે પ્રકારની વ્યતિકરણ ભાત સંપાત થાય છે. બંને પ્રકારનાં મધ્યસ્થ અધિક્તમ એકબીજા પર સંપાત થાય છે. તથા $590 \;nm$ તરંગલંબાઈવાળા પ્રકાશની ત્રીજી પ્રકાશિત શલાકા એ અજ્ઞાત તરંગલંબાઈવાળા પ્રકાશની યોથી પ્રકાશિત શલાકા સાથે સંપાત થાય છે. તો અજ્ઞાત પ્રકાશની તરંગલંબાઈ ($nm$ માં) કેટલી હશે?View Solution
- 8યંગ ડબલ સ્લિટના પ્રયોગમાં $450 \,nm$ તરંગલંબાઈ માટે, $2 \,m$ દૂર રખેલા પડદા ઉપર શલાકાની પહોળાઈ $0.35^{\circ}$ જેટલી મળે છે. આ આખીય રચનાને $7 / 5$ જેટલો વક્રીભવનાંક ધરાવતા માધ્યમમાં ડૂબાડવામાં આવે તો શલાકાની કોણીય પહોળાઈ $\frac{1}{\alpha}$ થાય છે. તો $\alpha$ નું મૂલ્ય ............ હશે.View Solution
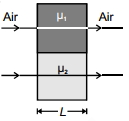
- 9શરૂઆતમા સમાન કળામા રહેલા બે પ્રકાશ કિરણો, આકૃત્તિમા દર્શાવ્યા પ્રમાણે $\mu_1$ અને $\mu_2\left(\mu_1\,>\,\mu_2\right)$ વક્રિભવનાંક ધરાવતા અને સમાન લંબાઈ $L$ ના બે માધ્યમમાંથી પસાર થાય છે. જો હવામા પ્રકાશ કિરણની તરંગલંબાઇ $\lambda$ હોય તો બહાર નિકળતા કિરણો વચ્ચે કળા તફાવત કેટલો છે ?View Solution
- 10યંગના ડબલ સ્લીટના પ્રયોગમાં $\lambda $ તરંગલંબાઈ ધરાવતા પ્રકાશને $d$ પહોળાઈની સ્લીટ પર પાડવામાં આવે છે જ્યાં $D$ ($D >> d >> \lambda $) એ સ્લીટ અને પડદા વચ્ચેનું અંતર છે. જો શલાકાની જાડાઈ $\beta$ હોય તો મહત્તમ તીવ્રતા ધરાવતા બિંદુ અને મહત્તમ તીવ્રતાથી અડધી તીવ્રતા ધરાવતા બિંદુ વચ્ચેનું અંતર કેટલું હશે?View Solution
