Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1પીક્રીક એસિડ, એસિટિક એસિડ અને ફિનોલના $ H_2O$ માં $ pK_a $ મૂલ્ય કયા ક્રમમાં છેView Solution
- 2View Solutionપ્રબળતાના વધવાના ક્રમમાં ક્રમ કયો છે

- 3View Solutionબેઝિક ક્ષમતાના ઘટતા ક્રમની ગોઠવણી કઈ છે ?
- 4View Solutionબેઝિક ક્ષમતાનો વધતો ક્રમ (ઓછો બેઝિક પ્રથમ) કયા સેટમાં દર્શાવ્યો છે ?
- 5બે સમઘટક $x$ અને $y$ની દહન ઉષ્મા અનુક્રમે $17$ કિલોજૂલ/જૂલ અને $12$ કિલોજૂલ /મોલ છે આ માહિતીમાંથી તે નિષ્કર્ષ પર આવી શકે છેView Solution
- 6View Solutionમહત્તમ કઈ સામગ્રી માં છે
- 7મુક્ત મૂલકના કયા બંધારણમાં મહત્તમ સંસ્પદન જોવા મળશે? $ [[\phi = C_6H_5]$View Solution
- 8View Solutionવધુ એસિડિક કયું છે ?
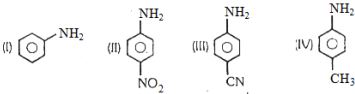
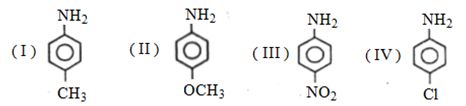
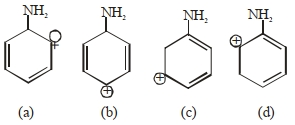
- 9વિસ્થાપિત એનિલીન ($I$ થી $IV$) ના બેઝિક ગુણધર્મનો સાચો ક્રમ કયો છે ?View Solution
- 10View Solutionસંકરણ અને સંસ્પંદન અસરને ધ્યાનમાં લેતા, બંધ લંબાઈ ઘટતી ક્રમમાં નીચેના બંધને ક્રમ આપો.
- 11સંક્રમણની સ્થિતિને ક્રમ આપો ક્રમમાં નીચેના પ્રતિક્રિયા પગલાં દરમિયાન થાય છેView Solution
વધતી સ્થિરતા ( ઓછા માં ઓછી થી વધારે સ્થાયી)$1. \,{H_3}C - \mathop O\limits^ + {H_2} \to CH_3^ + + {H_2}O$
$2.\,{(C{H_3})_3}C - \mathop O\limits^ + {H_2} \to {(C{H_3})_3}{C^ + } + {H_2}O$
$3.\,{(C{H_3})_2}CH - \mathop O\limits^ + {H_2} \to {(C{H_3})_2}C{H^ + } + {H_2}O$
- 12સંયોજન $(A)$ શું હશે ?View Solution
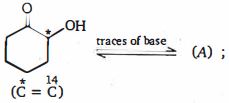
- 13સંયોજન માં ઇલેક્ટ્રોન અનુરાગી વિસ્થાપન થાય છે. વિસ્થાપક તરીકે મિથાઇલ $ -CH_2Cl, -CCl_3$ અને -$CHCl_2$ મળે છે. તો તેમને ઇલે.અનુરાગી વિસ્થાપન પ્રક્રિયા પ્રત્યેની પ્રક્રિયા માટે ચડતો ક્રમ કયો છે ?View Solution
- 14સૂચવેલા મુજબ, $C = C$ બંધ વિશે પરિભ્રમણ અવરોધના નીચેનામાંથી કયા ક્રમ યોગ્ય છે?View Solution
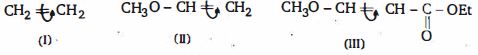
- 15View Solutionસૂર્યપ્રકાશમાં એલિવેટેડ તાપમાને ટોલ્યુઇન અને ક્લોરિનની પ્રક્રિયામાં રચાયેલી મધ્યવર્તી શું રજૂ કરે છે?
- 16View Solutionસૌથી એસિડિક પદાર્થ કયો છે ?
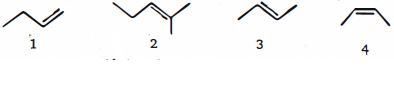
- 17View Solutionસૌથી પહેલા હાઇડ્રોજનની ઉષ્મામાં ઘટાડો કરવાના ક્રમમાં નીચે આપેલા આલકેન્સને ક્રમ આપો
- 18View Solutionસૌથી પ્રબળ એસિડ......... છે.
- 19સૌથી વધુ $K_a$ સાથે એસિડ પસંદ કરોView Solution
- 20View Solutionસ્થાયિતા ઉર્જાના ઘટતા ક્રમમાં નીચેના કાર્બોકેટાયન સૂચિ બનાવો.

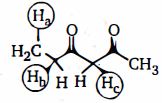
- 21હાઈડ્રોજન અણુઓને ક્રમ આપો $(H_a, H_b, H_c)$ તેમની એસિડિક પ્રબળતાના ક્રમમાં નીચેના કયા અણુમાં હાજર છે.View Solution
- 22View Solution
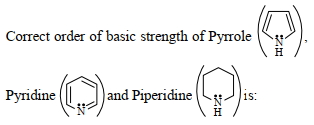
- 23$\mathrm{CH}_3-\mathrm{CH}=\mathrm{CH}-\mathrm{CHO}$ ના નીચે આપેલા સસ્પંદન બંધારણો નો સાચો સ્થિરતા ક્રમ શાધોView Solution
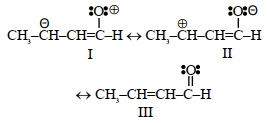
- 24આપેલ સંયોજનો માટે, ચઢતા $\mathrm{pK}_{\mathrm{a}}$ મૂલ્ય નો સાચો ક્રમ શોધો ?View Solution
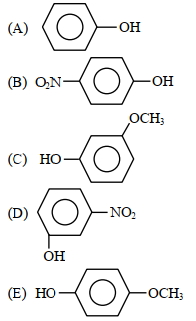
- 25View Solutionઉપરના સંયોજનો માટે ઈલેક્ટ્રોન અનુરાગી વિસ્થાપન ના ઉતરતા ક્રમ માટે સાચી ગોઠવણી શોધો.
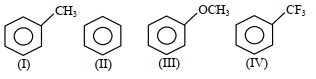
- 26View Solutionકાર્બએનાયન ની સ્થિરતા નો સાચો ક્રમ શોધો.
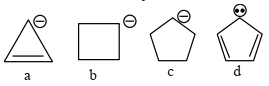
- 27View Solutionકાર્બોકેશાયન (કાર્બોકેટાયન) નો આકાર. . . . . . છે.
- 28View Solutionનીચે આપેલ માંથી કાબોકેશાયન (કેટાયન) ની સંખ્યા કે ને અતિસંયુગ્મન દ્વારા સ્થિરિકરણ પામતા નથી તે.......... છે.
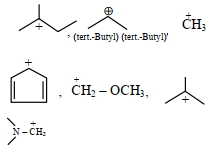
- 29View Solutionનીચે આપેલા પૈકી ક્યું ખોટું વિધાન છે ?
- 30નીચે આપેલા સંયુગ્મ બેઈઝો ની બેઝિક સામર્થ્ય ઘટતો ક્રમ શું થશે ?View Solution
${ }^{-} \mathrm{OH}, \mathrm{R} \overline{\mathrm{O}}, \mathrm{CH}_3 \mathrm{CO} \overline{\mathrm{O}}, \mathrm{C} \overline{1}$
- 31View Solutionનીચેના સંયુક્તો માંથી કેટલાક સંયુક્તો ઇન્ડક્ટિવ, મેઝોમેરીક અને હાયપરકન્જગેશન પ્રભાવો બતાવે છે?
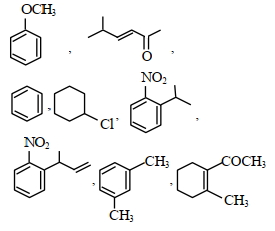
- 32View Solutionભાગ લેતા બંધારણોની સાપેક્ષ સ્થિરતા શોધો :
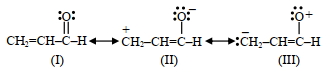
- 33View Solutionરીમાન - ટીમાન પ્રક્રિયામાં, એક મધ્યવર્તી દ્વારા ફીનોલનું પરિવર્તન સેલીસાલ્ડીહાઈડ માં થાય છે. મધ્યવર્તી નું બંધારણ શોધો.
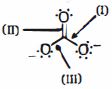
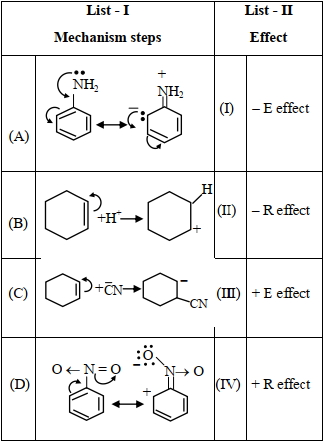
- 34સૂચિ $I$ સાથે સૂચિ $II$ ને જોડો.View Solution
(ઇમેજ)
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો
- 35View Solutionઆપેલ સંયોજન માટે વાસ્તવિક બંધારણ અને નીચી ઉર્જાવાળા સસ્પંદન બંધારણ વચ્ચે ઊર્જામાં તફાવત છે તે_________
- 36View Solutionઈલેકટ્રોન અનુરાગી વિસ્થાપન પ્રક્રિયા પ્રત્યેની સક્રિયતાનો ક્રમ જણાવો.
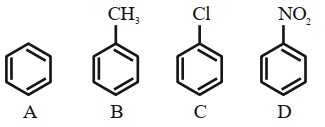
- 37કાર્બનની કઈ સ્પીસીઝ $e-$ નું ષષ્ટક ધરાવે છે અને ઈલેક્ટ્રોન અનુરાગી તરીકે વર્તે છે.View Solution
- 38View Solutionકાર્બોકેશાયનો (કાર્બોકિટાયનો)નો સાચો સ્થિરતા ક્રમ શોધો.
- 39View Solutionક્રિયાશીલ સમૂહ કે જે ઋણ સંસ્પંદન અસર દર્શાવે છે તે_________________.
- 40View Solution........................ ના વડે કાર્બનિક સંયોજનોની સાથે આયનીક પ્રક્રિયાઓ આગળ વધે છે.
(A) બંધ નું સમવિભાજન
(B) બંધ નું વિષમવિભાનન
(C) મૂક્ત મૂલક સર્જન (નિર્માણ)
(D) પ્રાથમિક મૂક્ત મૂલક
(E) દ્રીતીયક મૂક્ત મૂલક
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો :
- 41નિક્ટતમ પરમાણુ પર હાજર અબંધકારક ઈલેક્ટ્રોન યુગ્મ અને $\pi$ બંધ વચ્ચેની પારસ્પરિક ક્રિયા માટે જવાબદાર_____View Solution
- 42View Solutionનીચે આપેલ જુથ માંથી મેટા નિર્દેશક ક્રિયાશીલ સમૂહોનું જૂથ શોધો.
- 43નીચે આપેલ પૈકી, મેટા નિર્દેશક ક્રિયાશીલ સમૂહોની કુલ સંખ્યા __________છે. (પૂણાંક આધારિત)View Solution
$ -\mathrm{OCH}_3,-\mathrm{NO}_2,-\mathrm{CN},-\mathrm{CH}_3-\mathrm{NHCOCH}_3,$ $ -\mathrm{COR},-\mathrm{OH},-\mathrm{COOH},-\mathrm{Cl}$
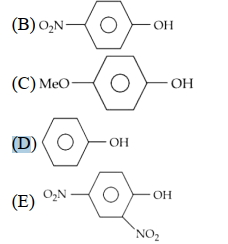
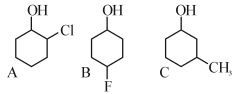
- 44નીચે આપેલ સંયોજનોમાં - $\mathrm{OH}$ સમૂહની એસિડિક્તાનો ચઢતો ક્રમ શોધો.View Solution
$(A)$ $\mathrm{Bu}-\mathrm{OH}$
$(B)$ $IMAGE$ $(C)$ $IMAGE$ $(D)$ $IMAGE$
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 45નીચે આપેલા $H$ પરમાણુઓનો ચઢતો એસિડિકતતા ક્રમ શોધો.View Solution
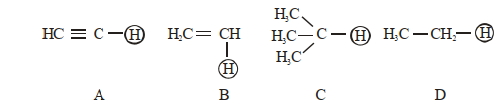
- 46View Solutionનીચે આપેલા પૈકી એરોમેટિક ઈલેકટ્રોનઅનુરાગી વિસ્થાપન પ્રક્રિયામાં અક્રિયકારક સમૂહોની કુલ સંખ્યા__________ છે.
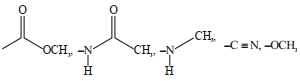
- 47View Solutionનીચે આપેલામાંથી ક્યાં માં હાઈડ્રોજન સૌથી વધુ એસિડિક છે ?
- 48View Solutionનીચે આપેલામાંથી ક્યા સંયોજન પર ઈલેક્ટ્રોન અનુરાગી વડે સૌથી સરળતાથી આક્રમાણ થઈ શકશે?
- 49View Solutionભાગ લેતાં બંધારણની સાપેક્ષ સ્થિરતાનો ક્રમ શોધો.
નીચે આપેલા વિકલપોમાંથી સાચો જવાબ પસંદ કરો.
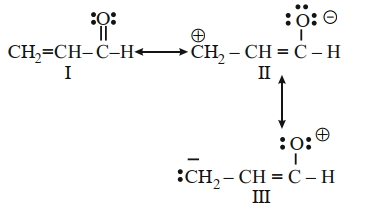
- 50View Solutionનીચે આપેલા કાર્બોકેટાયનો માટે હાઈડ્રોઈડ આકર્ષણ (બંધુતા)નો ઉતરતો ક્રમ શોધો.
નીચે આપેલા વિકલ્પોમાથી સાચો જવાબ પસંદ કરો.
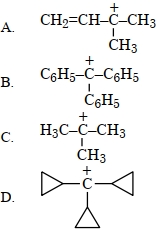
- 51View Solutionનીચે આપેલા માટે સૌથી વધુ સ્થાયી કાર્બોકેશાયન શોધી.
- 52View Solutionનીયે આપેલા સંયોજનો માટે ઈલેકટ્રોન અનુરાગી વિસ્થાપન તરફ સક્રિયતાનો ઉતરતો ક્રમ શોધો.
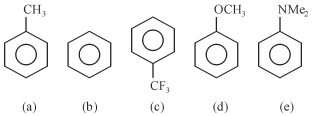
- 53View Solutionસસ્પંદ બંધારણોની સ્થિરતાનો ચઢતો ક્રમ શોધો.
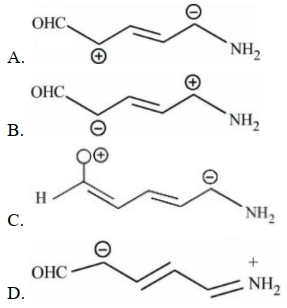
- 54View Solutionનીચે આપેલા સંયોજનોને એરોમેટિક ઇલેકટ્રોન અનુરાગી વિસ્થાપન પ્રક્રિયાના વેગના ચઢતાક્રમમાં ગોઠવો.
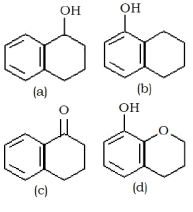
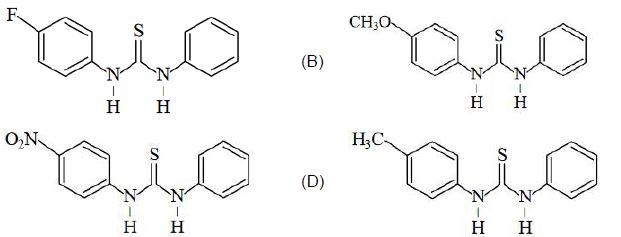
- 55નીચે બે વિધાનો આપેલા છે.એકને કથન $A$ વડે લેબલ કરેલ છે અને બીજાને કારણ $R$ વડે લેબલ કરેલ છે.View Solution
કથન $A:$ નીયે આપેલા સંયોજનો ની એસિડિક પ્રકૃતિ નો ક્રમ છે $A > B > C$.(આકૃતિ જુઓ)
કારણ $R$: ફ્લોરો એ ક્લોરો સમૂહ કરતાં પ્રબળ સામર્થ્યવાળો ઈલેકટ્રોન આકર્ષણ (ખેંચનાર) સમૂહ છે.
ઉપરના વિધાનોના સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી વધુ બંંધ બેસતો જવાબ પસંદ કરો.
- 56સૂચિ $I$ સાથે સૂચિ $II$ ને જોડો.View Solution
સૂચિ $I$ (એમાઈન) સૂચિ $II$ (pK_b) $A$ એનિલીન $I$ $3.25$ $B$ ઈથેનામાઈન $II$ $3.00$ $C$ $N-$ ઈથાઈલઈથેનામાઈન $III$ $9.38$ $D$ $N,N-$ ડાયઈથાઈલઈથેનામાઈન $IV$ $3.29$ નીચે આપેલ વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 57આપેલ સંયોજનમાં ઈલેક્ટ્રોનઅનુરાગી કેન્દ્રોની સંખ્યા $\dots\dots\dots$ છે.View Solution
- 58નાઈટ્રેશન તરફ સક્રિયતાના (reactivity) ચઢતા ક્રમમાં નીચેનાંને ગોઠવોઃView Solution
$A$. $p$-ઝાયલીન $B$. બ્રોમોબેન્ઝિન $C$. મેસિટિલિન $D$. નાઈટ્રોબેન્ઝિન $E$. બેન્ઝિન
નીચે આપેલા વિકલ્પોમાંથી યોગ્ય ઉત્તર પસંદ કરો.
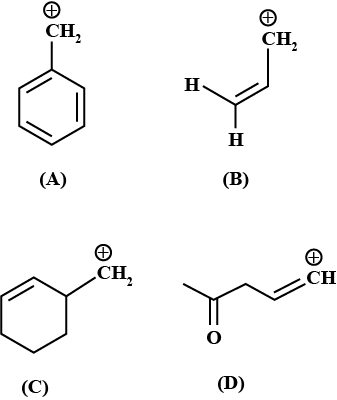
- 59નીચે આપેલ પૈકી કયું સૌથી વધુ સ્થાયી છે $?$View Solution
- 60View Solutionનીચે આપેલામાંથી કયો કાર્બોંકેટાયન વધુ સ્થાયી છે?
- 61View Solutionસ્થાયી કાર્બોકેટાયન જે ઉપરની પ્રક્રિયામાં બને છે તે શોધો.
- 62$\dot{ Cl }+ CH _{4} \rightarrow A + B$View Solution
ઉપરની વાતાવરણીય પ્રક્રિયાના તબક્કામાં $A$ અને $B$ શોધો.
- 63View Solutionકેન્દ્ર અનુરાગીનો સાચો ક્રમ કયો છે.
- 64નીચે આપેલા નિશાનીવાળા પ્રોટોનમાંથી ક્યું સંયોજન $pK _{ a }$ મૂલ્ય સૌથી ઓછુ પ્રદર્શિત કરે છે ?View Solution
- 65આજુબાજુના કેન્દ્રાનુરાગી ની સાચી જોડીઑ કઈ છેView Solution
$(A)$ $AgCN / KCN$
$(B)$ $RCOOAg / RCOOK$
$(C)$ $AgNO _{2} / KNO _{2}$
$(D)$ $AgI / KI$
- 66View Solutionઆપેલ આયનોમાં ક્યુ સંસ્પંદન સ્થાયી કાર્બોકેટાયન છે?
- 67View Solutionનીચેની સંસ્પંદન રચનાઓમાંથી કઈ સાચી નથી?
- 68નીચે બે વિધાનો આપવામાં આવ્યા છે:View Solution
વિધાન $I : C _{2} H _{5} OH$ અને $AgCN$ બંને કેન્દ્રાનુરાગી ઉત્પન્ન કરી શકે છે.
વિધાન $II : KCN$ અને $AgCN$ બંને બધી પ્રક્રિયાની પરિસ્થિતિઓ સાથે નાઇટ્રિલ કેન્દ્રાનુરાગી ઉત્પન્ન કરશે.
સૌથી યોગ્ય વિકલ્પ પસંદ કરો:
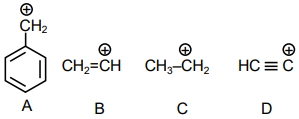
- 69View Solutionઆપેલ કાર્બોકેટાયનની સ્થાયીતાનો સાચો ક્રમ કયો છે:
- 70$\mathrm{CCl}_{4}, \mathrm{CHCl}_{3}$ and $\mathrm{CH}_{4}$ ની દ્વિધુવ ચાકમાત્રાનો ક્રમ જણાવો.View Solution
- 71$ S _ {N} 1$ પ્રક્રિયાની પદ્ધતિ આ પ્રમાણે આપવામાં આવી છેView Solution
$R - X \rightarrow R ^{\oplus} X ^{\ominus} \rightarrow R ^{\oplus} \| X ^{\ominus} \stackrel{ Y^\ominus }{\rightarrow} R - Y + X ^{\ominus}$
Ion pair Solvent separated ion pair
કોઈ વિદ્યાર્થી આપેલ પદ્ધતિના આધારે સામાન્ય લાક્ષણિકતાઓ આ રીતે લખે છે:
$(a)$ પ્રક્રિયા નબળા કેન્દ્રાનુરાગી દ્વારા તરફેણમાં છે
$(b)$ $R^ \oplus$ સરળતાથી પ્રક્રિયા કરી મોટુ સંયોજન આપે છે
$(c)$ પ્રક્રિયા રેસેમાઇઝેશન દ્વારા પૂર્ણ થાય છે
$(d)$ પ્રક્રિયા બિન-ધ્રુવીય દ્રાવક દ્વારા તરફેણ કરવામાં આવે છે.
કયા અવલોકનો યોગ્ય છે $?$
- 72નીચેના મધ્યસ્થી માટે બેઝિકતાનો વધતો ક્રમ ....(નિર્બળ થી પ્રબળ)View Solution
$(i)$ $\begin{array}{*{20}{c}}
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C{H_3}} \\
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|} \\
{C{H_3} - {C^ \mathbf{-} }} \\
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|} \\
{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C{H_3}}
\end{array}$$(ii)\;\;CH_2 = CH -\stackrel{\mathbf{-}}{C}H_2$
$(iii)\;\;CH \equiv \stackrel{\mathbf{-}}{C}$
$(iv)\;\;\stackrel{\mathbf{-}}{C}H_3$
$(v)\;\;\stackrel{\mathbf{-}}{C}N$
- 73View Solutionનીચેના આલ્કાઇનની દહન ઉષ્માનો સાચો ક્રમ જણાવો.
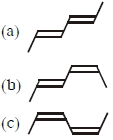
- 74આપેલા સંયોજનો $CH \equiv CH,\,C{H_3} - C \equiv CH,\,$ અને $C{H_2} = C{H_2}$ માટે તેમના એસિડ શક્તિનો સાચો ક્રમ નીચેનામાથી કયો થશે?View Solution
- 75View Solutionનીચેના પૈકી ક્યો સૌથી પ્રબળ એસિડ છે?
- 76View Solutionઇલેક્ટ્રોન અનુરાગી વિસ્થાપન પ્રક્રિયા પ્રત્યે નીચેના સંયોજનોની પ્રતિક્રિયાત્મકતાનો વધતો ક્રમ જણાવો.
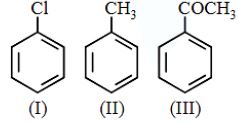
- 77View Solutionઇલેક્ટ્રોન અનુરાગી વિસ્થાપન પ્રક્રિયા પ્રત્યે નીચેના સંયોજનોની પ્રતિક્રિયાત્મકતાનો વધતો ક્રમ જણાવો.
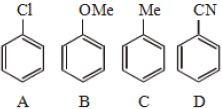
- 78નીચે આપેલા સંયોજનોમાં $pK_b$ નો વધતો ક્રમ શું હશે?View Solution
- 79નીચેના કેંદ્રાનુરાગી પ્રક્રિયકની કેન્દ્રાનુરાગીનો વધતો ક્રમ....View Solution
$(a)\,\,CH_3CO_2^-$ $(b)\,\,H_2O$
$(c)\,\,CH_3SO_3^-$ $(d)\,\,\bar OH$ - 80View Solutionનીચેના સંયોજનની પ્રબળ એસિડ સાથેની પ્રક્રિયામાં બંધના ખંડન માટે સૌથી વધુ અસર પામતુ સ્થાન જણાવો.
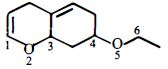
- 81View Solutionનીચેના પૈકી કયો અણુ સૌથી ઓછી સંસ્પંદનીય સ્થિરતા ધરાવે છે?
- 82View Solutionનીચેના પૈકી ક્યુ સંયોજન મહતમ દ્વિધુવ ચાકમાત્રા દર્શાવશે ?

- 83View Solutionનીચેના પૈકી ક્યુ સંયોજન મહત્તમ દ્વિધુવ ચાકમાત્રા દર્શાવે છે?
- 84નીચેના પૈકી કઇ જોડમાં $B$ કરતા $A$ વધુ સ્થાયી છે ?View Solution
$A$ || $B$
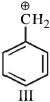
- 85નીચે આપેલ કાર્બોકેટાયનનો સ્થાયીતાનો ક્રમ કયો છે :View Solution
$(I)\,\,C{H_2} = CH - \mathop C\limits^ \oplus {H_2}$
$(II)\,\,C{H_3} - CH_2 - \mathop C\limits^ \oplus {H_2}$
- 86$( -)-1 -$ ક્લોરો ${-1}-$ ફિનાઇલ ઇથેનનું ટોલ્યુઇનમાં બનાવેલા દ્રાવણમાં થોડા પ્રમાણમાં ઉમેરેલા $SbCl_5$ ના કારણે ધીમું રિસેમિકરણ થાય છે, જે ....... ના સર્જનને લીધે થાય છે.View Solution
- 87View Solutionનીચેના અણુઓ માટે સ્થાયીતાનો સાચો ક્રમ (ઘટતો ક્રમ) ગોઠવો.
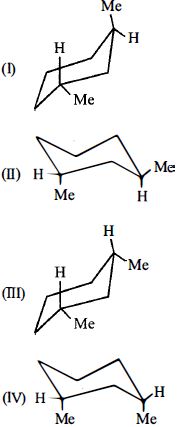
- 88View Solutionનીચેના સંયોજનોમાં ઇલેક્ટ્રોન અનુરાગી વિસ્થાપન પ્રક્રિયાઓમાં પ્રતિક્રિયાશીલતાનો યોગ્ય ક્રમ હશે
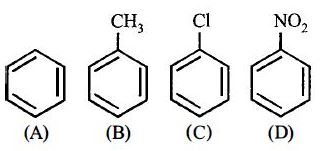
- 89View Solutionનીચે પૈકી કયું સૌથી વધારે સ્થિર છે?
- 90$1-$મિથોક્સી$-1, 3-$બ્યુટાડાઇનના નીચેનામાંથી સંસ્પંદનીય રચનાઓમાંથી કયું ઓછામાં ઓછું સ્થાયી છે?View Solution
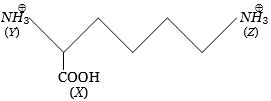
- 91નીચે આપેલા સંયોજનમાં$(X)$, $ (Y)$ અને $(Z)$ ની એસિડિટીનો યોગ્ય ક્રમ છે?View Solution
- 92View Solutionનીચે આપેલામાં, કયું સૌથી વધુ દ્વિધ્રુવ ચાકમાત્રા સાથેનું અણુ છે
- 93View Solutionનીચેનામાંથી કોણ સૌથી વધુ કેન્દ્રાનુરાગીતા ધરાવે છે?
- 94$D\,(+)$ $- 2-$ક્લોરો$-2-$ફિનાઇલ ઇથેનનું ટોલ્યુઇનમાં દ્રાવણ, $SbC{l_5}$ની ઓછી માત્રાની હાજરીમાં શું બનાવીને રેસેમીકૃત બને છે?View Solution
- 95નીચે આપેલ સમૂહમાંView Solution
$\begin{array}{*{20}{c}}{ - OAc}\\{\rm{I}}\end{array}$$\begin{array}{*{20}{c}}{ - OMe}\\{{\rm{II}}}\end{array}$$\begin{array}{*{20}{c}}{ - OS{O_2}Me}\\{{\rm{III}}}\end{array}$$\begin{array}{*{20}{c}}{ - OS{O_2}C{F_3}}\\{{\rm{IV}}}\end{array}$
સમુહ મુક્ત કરવાની ક્ષમતાનો ક્રમ શું છે?
- 96નીચેના સંયોજનો વચ્ચે એરોમેટિક ઇલેક્ટ્રોઅનુરાગી વિસ્થાપન તરફ ક્રિયાશીલતાનો ઘટતા ક્રમ શું છે?View Solution
$I.$ ક્લોરોબેન્ઝિન
$II.$ બેન્ઝિન
$III.$ એનિલિનિયમ ક્લોરાઈડ
$IV.$ ટોલ્યુઇન
- 97View Solutionનીચેની કયો સ્પીસીઝ સૌથી સ્થાયી છે?
- 98જે સ્થાયીતાનો ઘટતો ક્રમ છેView Solution
$(i)$ $C{H_3} - \mathop C\limits^ + H - C{H_3}$
$(ii)$ $C{H_3} - \mathop C\limits^ + H - O - C{H_3}$
$(iii)$ $C{H_3} - \mathop C\limits^ + H - CO - C{H_3}$
- 99ઇથેનમાં $C - C$ બંધનું Homolytic fission એક મધ્યવર્તી આપે છે જેમાં કાર્બન .... છે.View Solution
- 100નીચેના પરમાણુઓની $C - C$ બંધલંબાઈ ક્યા ક્રમમાં છે?View Solution