Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1View Solutionનીચે પૈકી જે કેન્દ્રાનુરાગી અને ઇલેક્ટ્રોનુરાગી બંને તરીકે વર્તે છે?
- 2$C{H_3}C{H_2}OH$ના કયા બંધમાં વિષમાંગ જોડાણ સૌથી સહેલાઇથી થાય છે?View Solution
- 3View Solutionપરમાણુનું સંસ્પંદન બંધારણ શું નથી ધરાવતું?
- 4View Solutionઆપેલ ધનાયનમાં, સૌથી સ્થાયી કાર્બોનિયમ આયન કયો છે?
- 5$1^° , 2^°, 3^°,$ અને $^{ \oplus} CH_3 $ કાર્બનકેટાયનના કાર્બનની સ્થિરતાનો ક્રમ કયો છે ?View Solution
- 6$C{H_3}C{H_2}I + KO{H_{(aq)}} \to C{H_3}C{H_2}OH + KI$ પ્રક્રિયાને નીચે દર્શાવેલા પૈકી શેમાં વર્ગીકૃત કરી શકાય છે ?View Solution
- 7$E^2$ એલિમીનેશનમાં ઘણાં પદાર્થો હૉફમાન નિયમને અનુસરે છે કે જેનો અર્થ.....View Solution
- 8$\overset{\oplus }{\mathop{C}}\,{{H}_{3}}\,$ નો આકાર કેવો છે?View Solution
- 9${{\text{3}}^ \circ }{\text{ , }}{{\text{2}}^ \circ }{\text{ ,}}{{\text{1}}^ \circ }$ અને $\mathop C\limits^ \bullet {{\text{H}}_{\text{3}}}$ માં કાર્બન મૂલકોની સ્થિરતાનો ક્ર્મ ક્યો છેView Solution
- 10View Solutionઅયુગ્મ ઈલેકટ્રોનની હાજરીના કારણે મુક્ત મૂલકો એ .........
- 11View Solutionઅયુગ્મિત ઇલેકટ્રૉનની હાજરીને લીધે મુકત મૂલકો ....... બને છે.
- 12આપેલ કાર્બોકેટાયન માટે સ્થિરતાનો સાચો કમ કયો છે ?$\mathop {\mathop C\limits^ \oplus {H_3}}\limits_{(i)} \,\,\,\,\,\,\,\,\,C{H_3}\mathop {\mathop C\limits^ \oplus {H_2}}\limits_{(ii)} \,\,\,\,\,\,\,\,\mathop {\mathop C\limits^ \oplus {H_2}}\limits_{(iii)} OC{H_3}\,$View Solution
- 13View Solutionઆપેલા પદાર્થોમાં એસિડિકતાનો સાચો ક્રમ કયો છે ?
- 14View Solutionઈલેકટ્રોઅનુરાગી કયો છે ?
- 15એ.....View Solution
$\begin{matrix}
\overset{\Theta }{\mathop{\overset{\centerdot \,\centerdot }{\mathop{C}}\,}}\,{{H}_{2}}-C-C{{H}_{3}} \\
|| \\
O \\
\end{matrix}$ અને $\begin{matrix}
C{{H}_{2}}=C-C{{H}_{3}} \\
| \\
:\underset{\Theta }{\mathop{\underset{\centerdot \,\centerdot }{\mathop{O}}\,}}\,: \\
\end{matrix}$ - 16View Solutionકઈ ખોટી ઈલેકટ્રોમેરિક અસર છે ?
- 17કયા સમૂહની જોડી $ (-I) $ અસર દર્શાવે છે ?View Solution
- 18View Solutionકયો એસિડ સૌથી પ્રબળ છે ?
- 19View Solutionકયો કાર્બોનીયમ આયન સૌથી ઓછો સ્થિર છે ?
- 20View Solutionકયો પદાર્થ ન્યુનતમ હાઈડ્રોજીનેશન ઉષ્મા ધરાવે છે ?
- 21View Solutionકયો પદાર્થ સૌથી નીચો ડાયપોલ મોમેન્ટ ધરાવે છે ?
- 22View Solutionકયો સમૂહ મહત્તમ અતિસંયુગ્મન અસર ધરાવે છે ?
- 23View Solutionકયો સૌથી એસિડિક પદાર્થ છે ?
- 24View Solutionકાર્બનના સંકરણમાં ફેરફાર થાય તેની સાથે કાર્બન આયનની સ્થિરતાનો ચડતો ક્રમ કયો છે ?
- 25View Solutionકાર્બનિક પદાર્થના ઈલેકટ્રોમેરિક અસર એ....
- 26View Solutionકાર્બેંએનાયન....
- 27View Solutionકાર્બોકેટાયનની સંકરણ અવસ્થા કઈ છે ?
- 28View Solutionકિટોનોમાંથી આયનો હાઈડ્રીનનું નિર્માણ એ શેનું ઉદાહરણ છે ?
- 29View Solutionકોના કારણે સંસ્પદન થાય છે ?
- 30View Solutionકોના દ્વારા ડાયપોલ મોમેન્ટ જોવા મળે છે ?
- 31ટોલ્યુઈનમાં $ (+) - 1 - $ક્લોરો $-1 - $ ફિનાઈલ ઈથેનનું દ્રાવણનું $ SbCl_5 $ ના થોડા મૂૂલ્યની હાજરીમાં ધાતુ રેસેમિકરણ થાય છે કારણ કે તેમાં......નું નિર્માણ થાય છે ?View Solution
- 32View Solutionતીર દ્વારા સૂચવવામાં આવેલ હાઇડ્રોજન ક્યાથી સરળતાથી દૂર થઈ જશે
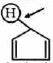
- 33View Solutionનીચેના ક્લોરો પદાર્થમાં કોણ નીચે ડાયપોલ મોમેન્ટ ધરાવે છે ?
- 34View Solutionનીચેના પદાર્થો માટે ઈલેકટ્રો અનુરાગી વિસ્થાપન પ્રક્રિયા માટે પ્રક્રિયા શીલતાનો સાચો ક્રમ કયો છે ?
- 35View Solutionનીચેના પૈકી કયું કાર્બોકેટાયન વધુ સ્થાયી છે ?
- 36View Solutionનીચેના પૈકી ક્યો સૌથી પ્રબળ મેટા- નિર્દેશક સમૂહ છે
- 37નીચેનામાંથી કયું $m-$ નિર્દેંશક સમૂહ નથી ?View Solution
- 38View Solutionનીચેનામાંથી કયો અણુ સૌથી વધુ ડાઈપોલ મોમેન્ટ ધરાવે છે ?
- 39નીચેનામાંથી કયો એસિડની $pK_a$ મૂલ્ય ધરાવે છે ?View Solution
- 40View Solutionનીચેનામાંથી કયો ક્રમ ઘટતી એસિડિકતાનો સાચો ક્રમ આપે છે ?
- 41View Solutionનીચેનામાંથી કયો સૌથી એસિડીક પદાર્થ છે ?
- 42View Solutionનીચેનામાંથી કયો સૌથી ઓછો બેઝિક છે ?
- 43View Solutionનીચેનામાંથી કયો સૌથી પ્રબળ એસિડ છે ?
- 44View Solutionનીચેનામાંથી કયો સૌથી પ્રબળ બેઇઝ છે ?
- 45View Solutionનીચેનામાંથી કયો સૌથી બેઝિક પદાર્થ છે ?
- 46View Solutionનીચેનામાંથી કયો સૌથી સ્થિર કાર્બોએનાયન છે ?
- 47View Solutionનીચેનામાંથી કોણ સૌથી ઓછો એસિડિક છે ?
- 48પ્રક્રિયાનો દર ઝડપી તો જ્યારે $Z$ એ.....View Solution
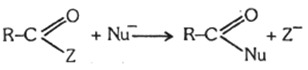
- 49પ્રોપિન અને $HCl $ વચ્ચેની પ્રક્રિયાથી મળતો આઇસોપ્રોપાઇલ ક્લોરાઇડ નીચેનામાંથી કોના આધારે મળે છે ?View Solution
- 50View Solution....... માં બધી જ કાર્બન -કાર્બન બંધ લંબાઈઓ સમાન હોય છે.
- 51View Solutionસિગ્મા બંધ કક્ષકોમાં ભાગ લેતા વિસ્થાનીકૃતનો પ્રકારને શું કહે છે ?
- 52View Solutionસૂર્યપ્રકાશ વડે કેવા પ્રકારનું વિભાજન શક્ય છે ?
- 53View Solutionસૌથી સ્થિર કાર્બએનાયન કયો છે ?
- 54View Solutionસૌથી સ્થિર કાર્બન કેટાયન કયો છે ?
- 55$1 $ થી $4 $ પદાર્થોનાં $ HCN $ ઉમેરતાં વધતો દર કયો છે ?View Solution
$1.$ $HCHO$
$2.$ $ CH_3COCH_3$
$3.$ $PhCOCH_3$
$4.$ $PhCOPh$
- 56$A, B,$ and $C$ની વચ્ચે કાર્બન-કાર્બન બંધ પરિભ્રમણની તુલના કરોView Solution
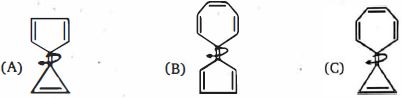
- 57$\mathop {C{H_2} = CH - CH = CH{ - ^ \oplus }N{H_3};}\limits_{(I)} \,\,\mathop {{\,^ \oplus }C{H_2}-CH = CH{ - ^\circleddash }CH{ - ^ \oplus }N{H_3}}\limits_{(II)} $View Solution
$\mathop {^ \oplus C{H_2} - CH = CH - CH = N{H_3}}\limits_{(III)} $
આમાંથી કયું બંધારણ માન્ય માન્ય પ્રામાણભૂત બંધારણ નથી?
- 58$\mathop O\limits^\Theta H\,\,,\,\,\mathop N\limits^\Theta {H_2},\,\,HC\,\, \equiv \,\,\mathop C\limits^\Theta \,,\,\,C{H_3} - \mathop C\limits^\Theta {H_2}\,$ બેઝિક ક્ષમતાનો ઘટતોક્રમ ક્યો છે?View Solution
- 59$A - D$, ના જુથ માં બેઝિક પ્રબળતા સંબંધિત માત્ર એક જ જુથ ખોટુ છે. તેને પસંદ કરોView Solution
- 60$x, y$ અને $z$ બેઝિક પ્રબળતા માં ઘટાડોનો યોગ્ય ક્રમ કયો છે ?View Solution
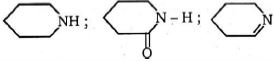
- 61$NH_2, -OCH_3, -C_6H_5$ અને $-NO_2$ સમુહની નિદર્શન ક્રમ નીચે મુજબ ક્રમમાં છે.View Solution
- 62$O{H^ - },\,\,NH_2^ - \,,HC\,\, \equiv \,\,{C^ - }\,,\,\,C{H_3}\, - \,\,CH_2^ - $ બેઈઝની પ્રબળતાનો ઘટતો ક્રમ કયો છે ?View Solution
- 63$p$ નાઈટ્રોફિનોકસાઈડ આયનનું સંસ્પદન બંધારણનું સૌથી યોગ્ય નિરૂપણ કયું છે ?View Solution
- 64અગ્રતાનો સાચો ક્રમ. જૂથોના $-SCH_3 \,(I), -NO_2\, (II), -C \equiv CH \,(III)$ અને $-CH_2C_6H_5 \,(IV)$, વર્ગીકરણના આધારે કયો છે (વધતો ક્રમ )View Solution
- 65View Solutionઆ અણું ના વર્તુળ એ વધારે બેઝિક અણું તરીકે વર્તે છે .નીચેનામાંથી કઈ સાચી રજૂઆત છે
- 66View Solutionઆપેલ અણુની સૌથી સ્થાયી પ્રમાણભૂત રચના કઈ છે:
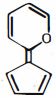
- 67View Solutionઆપેલ પ્રક્રિયાને કઇ ઉર્જા આકૃતિ શ્રેષ્ઠ રજૂ કરે છે?
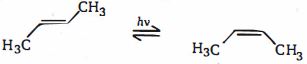
- 68View Solutionઆપેલ બંધારણ વચ્ચે સૌથી સ્થાયી પ્રમાણભૂત બંધારણ કયું છે
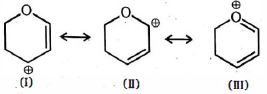
- 69આપેલ સંયુગ્મિત બેઈઝ $ (R = CH_3) $ ની વધતી બેઝીકતાનો સાચો ક્રમ કયો છે ?View Solution
- 70આપેલ સંયોજનમાં $\alpha$ -હાઇડ્રોજનની કુલ સંખ્યા કેટલી છેView Solution
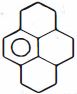
- 71View Solutionઆપેલ સંયોજનમાં બે ને પસંદ કરો જે આયનીકરણ પર સમાન કાર્બોકેટાયનઆપે છે.
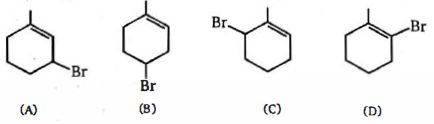
- 72View Solutionઆપેલ સંયોજનોની બેઝિક પ્રબળતાની તુલના કરો:

- 73View Solutionઆપેલ સંયોજનોમાં, એનોલ સામગ્રીનો યોગ્ય ક્રમ કયો છે
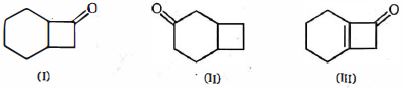
- 74View Solutionઆપેલ સંયોજનોમાં, એનોલ સામગ્રીનો યોગ્ય ક્રમ કયો છે
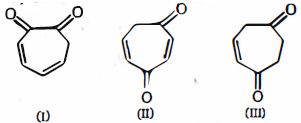
- 75View Solutionઆપેલા જૂથમાં, કયું જે સંસ્પંદનીય બંધારણનું પ્રતિનિધિત્વ કરે છે?
- 76આપેલા પરમાણુના નામાંકનમાં, $H$ અણું શામેલ છેView Solution
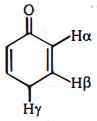
- 77View Solutionઆપેલા પ્રમાણભૂત બંધારણણો સાચો સ્થાયિતા ક્રમ કયો છે ?

- 78View Solutionઆયનોની કેટલીક જોડી નીચે આપેલ છે. કઈ જોડીમાં, પ્રથમ આયન બીજા કરતા વધુ સ્થિર છે?
- 79ઈલેકટ્રોનુરાગી $\mathop N\limits^ \oplus {O_2}$ નીચેનામાંથી કોની સાથે પ્રક્રિયા કરે છે. $\mathop N\limits^ \oplus {O_2}$એ કયા કિસ્સામાં મેટા સ્થાનમાં પ્રક્રિયા કરશે.View Solution
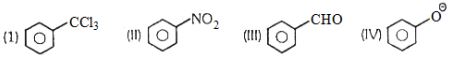
- 80ઈલેકેટ્રોન અનુરાગી $ E^{\oplus} $ બેન્ઝિન ચક્ર પર હુમલો કરીને મધ્યવર્તીં $ \sigma -$ સંકીર્ણ બનાવે છે. તેમાંથી કયો $\sigma - $ સંકીર્ણ સૌથી ઓછી ઉર્જા ધરાવે છે ?View Solution
- 81View Solutionએસિડ પ્રબળતા ઓછી થવાના ક્રમમાં નીચેના સંયોજનો ક્રમ આપો મોટાભાગે એસિડિક થી ઓછામાં ઓછું એસિડિક)
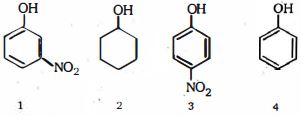
- 82એસિડ સાથેની પ્રક્રિયા પર, $4$ -પાયરોન ખૂબ જ સ્થિર ધનાયન નીપજ આપે છે.નીચેનામાંથી કયું બંધારણ પ્રોટોનેશન બાજુને તે નીપજ બતાવે છે?View Solution
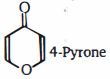
- 83View Solutionએસિડિક શરતો હેઠળ આયનીકરણ ની સરળતાના ઘટતા ક્રમમાં નીચેના આલ્કોહોલને ગોઠવો.
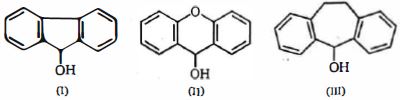
- 84View Solutionએસિડિટી (પ્રથમ નબળા એસિડ) ની ક્રમમાં નીચેના સંયોજનો ક્રમ આપો
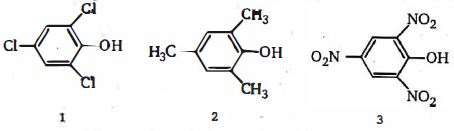
- 85View Solutionએસિડ્સની કેટલીક જોડીઓ નીચે આપેઌ છે. તે જોડી પસંદ કરો જેમાં પ્રથમ એસિડ વધુ પ્રબળ હોય
- 86View Solutionકયામાં દ્વિ-ધ્રુવીય ચાકમાત્રા મહત્તમ છે?
- 87View Solutionકયા સંયોજનમાં સૌથી વધુ દ્વિધ્રુવી ચાકમાત્રા છે?
- 88કાર્બાનિયનની સ્થિરતાનો ઘટતો ક્રમ નીચેનામાંથી કયો છે ?View Solution
$(1)\,\,{{(C{{H}_{3}})}_{3}}\bar{\ddot{C}}$
$(2)\,\,{{(C{{H}_{3}})}_{2}}\bar{\ddot{C}}$
$\,(3)\,\,C{{H}_{3}}\bar{\ddot{C}}{{H}_{2}}$
$(4)\,\,{{C}_{6}}{{H}_{5}}\bar{\ddot{C}}{{H}_{2}}$
- 89View Solutionકેન્દ્રઅનુરાગી વિરથાપન પ્રક્રિયા માટે નીચેના પૈકી કોણ સૌથી સક્રિય છે ?
- 90છ હાઇડ્રોકાર્બન માટે પસંદ કરેલા બંધ કોણ નીચે દર્શાવવામાં આવ્યા છે. આ હાઇડ્રોકાર્બન્સને તેમના $pK_a$ મૂલ્યો અનુસાર, નીચાથી ઉચ્ચતમ સુધી ગોઠવોView Solution
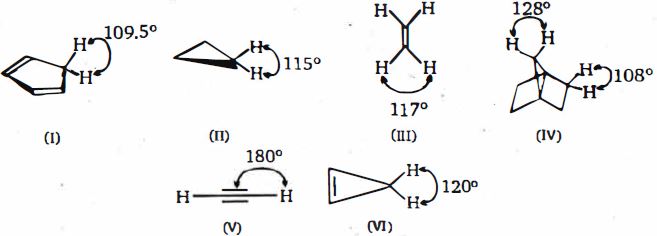
- 91જ્યારે નીચેની પદ્ધતિ પર $E^+$ હુમલો કરે છે ત્યારે $o/ p$ ગુણોતર નો યોગ્ય ક્રમ કેટલો છે?View Solution
$\underset{A}{\mathop{PhF}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underset{B}{\mathop{PhCl}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underset{C}{\mathop{PhBr}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underset{D}{\mathop{PhI}}\,$
- 92View Solutionતીર સાથે સૂચવેલ બંધના બંધ વિયોજન ઉર્જાને ક્રમ આપો (નાનાથી મોટા સુધી)
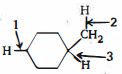
- 93તેની મૂળ પ્રબળતા $I$ - ડાયમિથાઇલ એમિનો નેપ્થાલિન કરતા વધુ $10^{10}$ છે. ઉચ્ચ બેઇઝ પ્રબળતા નું કારણ છેView Solution
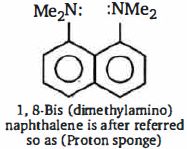
- 94View Solutionતેમની વ્યક્તિગત સ્થિરતા માટે ફોર્મિક એસિડની નીચેની ગુંજારિત રચનાઓની તપાસ કરો અને પછી નીચે આપેલા સવાલનો જવાબ આપો.
નીચે આપેલમાંથી કઈ ગોઠવણી ઉપરોક્ત સંસ્પંદન ફાળો આપનારાઓની સ્થિરતામાં ઘટાડો કરવાનો યોગ્ય ક્રમ આપે છે?
- 95ધન ભાર કરાયેલ $C_2H_3$ ઘટકો નો વિચાર કરો જેમાં ધન થયેલ કાર્બન $sp$ છે - સંકરિત, બિનભાર કાર્બન $sp^2$ સંકરિત છે અને ખાલી $\pi$ કક્ષક પદ્ધતિ માટે લંબ છે . તે આ કેટાયન શ્રેષ્ઠ વર્ણન શું છે?View Solution
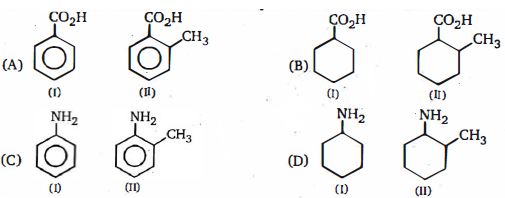
- 96નીચે આપેલી જોડીઓ માં $(A)$ અને $(B)$ માં વધુ એસિડિક અને $(C)$ અને $(D)$ માં વધુ બેઝિક શોધોView Solution
- 97View Solutionનીચે દર્શાવેલા કયા બંધારણમાં, જેની સંભવિત ઉર્જા ઓછી છે?
- 98View Solutionનીચેના કાર્બોકેટાયન માંથી કયું એક સૌથી લાંબી અર્ધ આયુષ્ય ધરાવે છે?
- 99નીચેના કેન્દ્રાનુરાગીમાંથી કેન્દ્રાનુરાગીનો ઘટતો ક્રમ કયો છે ?View Solution
$1.\,\,\,\begin{array}{*{20}{c}}
{C{H_3} - C - {O^ - }} \\
{\,\,\,||} \\
{\,\,\,O}
\end{array}$ $2.\,\,CH_3O^-$ $3.\,\,CN^-$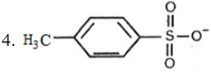
- 100નીચેના પદાર્થમાં કાર્બન - કાર્બન એક બંધ લંબાઈનો ઘટતો ક્રમ કયો છે ?View Solution
$(I)$ $CH_2 = CH - C \equiv CH$
$(II)$ $CH \equiv C - C\equiv CH$
$(III)$ $CH_3 - CH = CH_2$
$(IV) $ $CH_2 = CH - C = CH_2$