Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1View Solutionઝિંકની અશુદ્ધિ ધરાવતા કોપરના નમૂનાનુ વિધુતવિભાજન દ્વારા શુદ્ધિકરણ કરતા વિધુતધ્રુવો શુ હશે ?
કેથોડ , એનોડ
- 2ડાબા અને જમણા વિધુતધ્રુવના રિડક્શન પોટેન્શિયલના સંદર્ભમાં કોષનો $EMF$ .. . . થશે.View Solution
- 3$Pt|{H_2}({P_1})|{H^ + }_{(aq)}||{H_2}({P_2})|Pt$ કોષનો $emf$ કેટલો થશે ?View Solution
- 4વાહકતા $(unit \,Siemens\, S)$ એ પાત્રનું ક્ષેત્રફળ અને તેમાંના દ્રાવણની સાંદ્રતાના સમપ્રમાણમાં તથા પાત્રની લંબાઇના વ્યસ્ત પ્રમાણમાં હોય છે. તો સપ્રમાણતા અચળાંકનો એકમ. . . . થશે.View Solution
- 5$E_{F{e^{3 + }}|\,Fe}^0 = - \,0.036{\mkern 1mu} \,V$ અને $E_{F{e^{2 + }}|\,Fe}^0 = - \,0.439{\mkern 1mu} \,V$ છે, તો $Fe^{3+} + e^{-} \rightarrow Fe^{2+}$ પ્રક્રિયા માટે $E^{o}_{Cell} = $ .......... $\mathrm{V}$View Solution
- 6$Fe(OH)_2$ એ $Fe(II)$ દ્રાવણથી અવક્ષેપિત થાય છે જ્યારે થોડા ઘન બને છે પણ ઘેરા લીલા તરીકે થઈ જાય છે અને પછી ભુરા થાય છે કોના કારણે...View Solution
- 7$NiSO_4$ અને $CuSO_4$ ના દ્રાવણ ભરેલા બે કોષને શ્રેણીબદ્ધ કરી વિદ્યુતપ્રવાહ પસાર કરતાં $1.6$ ગ્રામ $Cu$ વિદ્યુતધ્રુવ પર જમા થાય ત્યારે કેટલી$Ni$ ધાતુ ઉદભવે ? જો $NiSO_4$ ને બદલે $AgNO_3$ નું દ્રાવણ ભરેલો કોષ જોડવામાં આવે, તો સિલ્વર કેટલા ગ્રામ મળે ? [પરમાણુભાર :$ Cu = 63.5$ ગ્રામ/મોલ, $Ni = 58.7$ ગ્રામ/મોલ, $Ag = 108$ ગ્રામ/મોલView Solution
- 8આર્હૅનિયસ સમીકરણ સાથે $\ln k$ વિરુદ્દ $\frac{1}{T}$ નો કયો આલેખ સંગત (consistent) છે?View Solution
- 9જ્યારે તાપમાનમાં $27^{\circ} \mathrm{C}$ થી $57^{\circ} \mathrm{C}$ ફેરફાર થાય છે ત્યારે પ્રક્રિયાનો વેગ (દર) ચાર ગણો થાય છે. સક્રિયકરણ શક્તિની ગણાતરી કરો.View Solution
( $\mathrm{R}=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}, \log 4=0.6021$ આપેલ છે.)
- 10View Solution..............નું મૂલ્ય જાણતા હોય તો કોઈ પણ રાસાયણિાક પ્રક્રિયાની સક્રિયકરણ શક્તિની ગણાતરી કરી શકાય છે.
- 11એક નિશ્ચિત પ્રક્રિયાં માટે, વેગ = $k [ A ]^2[ B ]$ છે.$B$ની સાંદ્રતા અચળ રાખીને જ્યારે $A$ની પ્રારંભિક સાંદ્રતા ત્રણ ગણી કરવામાં આવે ત્યારે પ્રારંભિક વેગ થશે તે...View Solution
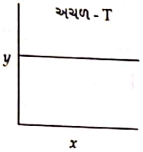
- 12આપેલ આલેખ પ્રક્રિયાની ગતિકી દર્શાવે છે.View Solution
શૂન્ય અને પ્રથમક્રમ પ્રક્રિયા માટે $y$ અને $x$ અક્ષો અનુક્રમે...
- 13એક પ્રથમક્રમ પ્રક્રિયા $A \rightarrow$ નીપજો માટે, $A$ની પ્રારંભિક સાંદ્રતા $0.1\,M$ છે, જે $5$ મિનિટો પછી $0.001 \,M$ થાય છે. પ્રક્રિયા માટે વેગ અચળાંક $min ^{-1}$માં શોધો.View Solution
- 14$\mathrm{A} \rightarrow \mathrm{B}$ પ્રક્રિયા માટે, પ્રક્રિયાની એન્થાલ્પી $-4.2\, \mathrm{~kJ}$ mol $^{-1}$ અને સક્રિયકરણ એન્થાલ્પી એ $9.6\, \mathrm{~kJ} \mathrm{~mol}^{-1}$ છે. પ્રક્રિયા માટેની સાચી સ્થિતિ ઊર્જા છબી (profile) વિકલ્પમાં દર્શાવેલ છે.View Solution
- 15પ્રથમ ક્રમ પ્રક્રિયાનો આર્હેનિયસ આલેખ $\left(\ln \mathrm{k}\,\, \mathrm{v} / \mathrm{s} \,\,\frac{1}{\mathrm{~T}}\right)$નો ઢાળ $-5 \times 10^{3} \,\mathrm{~K}$ છે. પ્રક્રિયાના $\mathrm{E}_{\mathrm{a}}$ નું મૂલ્ય શું છે ? તમારા જવાબ માટે સાચો વિકલ્પ પસંદ કરો.($\mathrm{~kJ} \mathrm{~mol}^{-1}$ માં)View Solution
$\left[\right.$ આપેલ $\left.\mathrm{R}=8.314 \,\mathrm{JK}^{-1} \,\mathrm{~mol}^{-1}\right]$
- 16View Solutionએક પ્રક્રિયાના પ્રક્રિયકની સાંદ્રતામાં થતો વધારો નીચેના માંના ફેરફાર તરફ દોરી જશે જે શોધો:
- 17એક પ્રથમ ક્રમની પ્રક્રિયા માટે વેગ અચળાંક $4.606 \times 10^{-3} s ^{-1} $. પ્રક્રિયાનાં $2.0\, g$ માંથી $0.2\, g$માં થતાં ઘટાડા માટે ......... $s$ સમય જરૂરી છે?View Solution
- 18પ્ર્કિયકની શરૂઆતની સાંદ્રતા $0.02\, M$ ધરાવતા એક શૂન્ય ક્રમની પ્રક્રિયાનો અર્ધઆયુષ્ય સમય $100\, s$ છે. તો પ્રક્રિયા માટે વેગ અચળાંક ($mol\, L ^{-1} s ^{-1}$ માં$)$ જણાવો.View Solution
- 19રાસાયણિક પ્રક્રિયાઓના અથડામણ સિદ્ધાંતમાં, $Z_{\text {AB }}$ ............. રજૂ કરે છેView Solution
- 20પ્રથમ ક્રમ ની પ્રકિયા નો અચળ વેગ $\mathrm{k}$ છે સમય $(t)$ $99 \%$ પ્રકિયા પૂર્ણ કરવા માટે લાગતો સમય છે તો પ્રકિયા કઈ હશે ?View Solution
- 21પ્રથમ ક્રમ ની પ્રકિયા માટે અચલ વેગ $2.303 \times 10^{-3} \;\mathrm{s}^{-1} .$ છે $40 \mathrm{g}$ પ્રકીયક ને $10\; \mathrm{g}$ પ્રકિયા થવા માટે લાગતો સમય........$s$View Solution
[અહી આપેલ $\left.\log _{10} 2=0.3010\right]$
- 22અર્ધ આયુષ્યના કિરણોત્સર્ગી નમૂના માટે ત્વરિત સમયે કિરણોત્સર્ગી વિઘટનનો દર$2.2 \times 10^{9}\; \mathrm{s}$$10^{10} \;\mathrm{s}^{-1}$છે .તે ઇન્સ્ટન્ટમાં તે નમૂનામાં કિરણોત્સર્ગી અણુઓની સંખ્યા કેટલી છે ?View Solution
- 23પ્રકિયા માટે સક્રિયકરણ ઉર્જા $\mathrm{E}_{\mathrm{a}}=0$ અને $200\; \mathrm{K}$ તાપમાને અચળ વેગ $1.6 \times 10^{6} \;\mathrm{s}^{-1} .$ $400\; \mathrm{K}$ તાપમાને અચળ વેગે વાયુ ના અચળાંક નું મૂલ્ય શું હશે ?View Solution
$\mathrm{R}=8.314\; \mathrm{JK}^{-1} \mathrm{mol}^{-1}$
- 24રસાયણિક પ્રકિયા માટેView Solution
$\mathrm{N}_{2}(\mathrm{g})+3 \mathrm{H}_{2}(\mathrm{g}) \rightleftharpoons 2 \mathrm{NH}_{3}(\mathrm{g})$
સાચો વિકલ્પ કયો છે ?
- 25View Solutionજ્યારે પ્રક્રિયાની પ્રારંભિક સાંદ્રતા બમણી કરવામાં આવે ત્યારે શૂન્ય ક્રમની પ્રક્રિયાનો અર્ધઆયુષ્ય સમય ......
- 26View Solutionપ્રથમ અને દ્વિતીય ક્રમની પ્રક્રિયાઓ વચ્ચે સાચો તફાવત
- 27પ્રથમ ક્રમની પ્રક્રિયાનો વિશિષ્ટ પ્રક્રિયાવેગ $10^{-2}\, sec^{-1}$ છે. તો પ્રક્રિયકના $20\, g$ ઘટીને $5\, g$ થવા માટે ........ $\sec$ લાગશે.View Solution
- 28અનુમાનિત પ્રક્રિયા $X_2 + Y_2 \rightarrow 2XY,$ ની ક્રિયાવિધિ નીચે આપેલી છે.View Solution
$(i)\,\, X_2 \rightarrow X + X$ $($ઝડપી$)$
$(ii)\,\,X + Y_2 \rightleftharpoons XY + Y$ $($ધીમી$)$
$(iii)\,\,X+ Y \rightarrow XY$ $($ઝડપી$)$
તો કુલ પ્રક્રિયાક્રમ જણાવો.
- 29ઓછા દબાણ પર ટંગસ્ટન પર ફોસ્ફિન $(PH_3)$ ના વિઘટન એ પ્રથમ ક્રમની પ્રક્રિયા છે.કારણ કે.....View Solution
- 30View Solutionરાસાયણિક પ્રક્રિયા દરમિયાન ઉદીપકનો ઉમેરો નીચેનામાંથી કયા જથ્થામાં ફેરફાર કરે છે
- 31પ્રથમ ક્રમની એક પ્રક્રિયાની શરૂઆત બાદ $10$ સેકન્ડે પ્રક્રિયાનો વેગ $0.04\, mol \,L^{-1} \,s^{-1}$ છે. અને $20$ સેકન્ડે $0.03\, mol \,L^{-1} \,s^{-1}$ છે. તો પ્રક્રિયાનો અર્ધઆયુષ્ય સમય .............. $\sec$ થશે.View Solution
- 32View Solutionજો પ્રક્રિયામાં પ્રક્રિયકની શરૂઆતની સાંદ્રતા બે ગણી કરવામાં આવે તો પ્રક્રિયાના અર્ધઆયુષ્ય સમયને અસર થતી નથી. તો પ્રક્રિયાનો ક્રમ ........... થશે.
- 33View Solutionનીચેના પૈકી ક્યા આલેખના ઢાળ પરથી પ્રક્રિયાની સક્રિયકરણ ઊર્જા ગણી શકાય છે ?
- 34પ્રકિયા $A\rightarrow B$ નો વેગ અચળાંક$0.6 \times 10^{-3}\, mol\, L^{-1}\, s^{-1}.$ છે જો $A$ ની સાંદ્રતા $5\, M,$ છે ત્યારબાદ $20$ મિનિટ પછી $B$ ની સાંદ્રતા .......$M.$ હશેView Solution
- 35$A$ તથા $B$ વચ્ચેની પ્રક્રિયામાં $A$ ના સંદર્ભમાં પ્રક્રિયાક્રમ $2$ છે. તથા $B$ ના સંદર્ભમાં પ્રક્રિયાક્રમ $3$ છે. જો $A$ તથા $B$ બંનેની સાંદ્રતા બમણી કરવામાં આવે તો પ્રક્રિયાક્રમ .............. ના ગુણકથી વધશે.View Solution
- 36એક પ્રક્રિયા $2$ કલાકમાં $50 \%$ પૂર્ણ થાય છે. તથા $4$ કલાક માં $75 \%$ પૂર્ણ થાય છે. તો પ્રક્રિયાનો ક્રમ ..........View Solution
- 37જો તાપમાન $20\,^oC$ થી વધી $35\,^oC$ થતા પ્રક્રિયાનો વેગ બે ગણો થતો હોય તો પ્રક્રિયાની સક્રિયકરણ ઊર્જા ........... $kJ \,mol^{-1}$ થશે.View Solution
$(R = 8.314\, J \,mol^{-1}\, K^{-1})$
- 38${}^{14}C$ ના રેડિયોએક્ટિવ ક્ષયનનો અર્ધઆયુષ્ય સમય $5730$ વર્ષ છે. એક પુરાતત્ત્વીય કલાકૃતિમાં રહેલા લાકડામાં જીવંત ઝાડની સરખામણીમાં $80\%$ ${}^{14}C$ હોય, તો નમૂનાનુ આયુષ્ય ......... $years$ ગણો.View Solution
- 39$25\,^oC$ એ દર અચળાંક, સક્રિયકરણ ઊર્જા અને રાસાયણિક પ્રક્રિયાનાં આર્હેંનિયસ પરિબળો અનુક્રમે $3.0\times 10^{-4} \,s^{-1}, 104.4 \,kJ$ મોલ$^{-1} $ અને $6.0 \times 10^{14}\, s^{-1}$ છે. તો $T\rightarrow \infty$ તરીકે દર અચળાંકનું મૂલ્ય શોધો.View Solution
- 40$25\,^oC$ તાપમાને એક પ્રક્રિયાનો વેગ અચળાંક $1 \times 10^{-3}\,s^{-1}$ છે. જો તાપમાન વધારીને $35\,^oC$ કરતા પ્રક્રિયાનો વેગ બમણો થતો હોય, તો આ પ્રક્રિયાની સક્રિયકરણ ઊર્જા .......... $kJ\, mol^{-1}$ થશે.View Solution
- 41$273\, K$ તાપમાને એક પ્રક્યિાનો વેગ $R_0$, છે. તો $313\, K$ તાપમાને પ્રક્રિયાનો વેગ કેટલો થશે ? (તાપમાન ગુણક $2$ લેવો)View Solution
- 42$298\, K$ તાપમાને ઇથિનની હાઇડ્રોજિનેશન પ્રક્રિયામાં $50\, min$ માં હાઇડ્રોજનના મોલ $2.2$ માંથી ઘટીને $1.4$ થાય તો મોલ/સેકંડ એકમમાં પ્રકિયા વેગ જણાવો.View Solution
- 43$2A + B \rightarrow $ નિપજ પ્રક્રિયા માટે દર અચળાંક $(K) 15$ સેકન્ડ પછી $2.5 × 10^{-5}$ લીટર મોલ$^{-1}$ સેકન્ડ છે, $30$ સેકન્ડ પછી $2.60 × 10^{-5}$ લીટર મોલ$^{-1}$ સેકન્ડ$^{-1}$ છે અને $50$ સેકન્ડ પછી $2.55 × 10^{-5}$ લીટર મોલ$^{-1}$ સેકન્ડ$^{-1}$ છે. તો પ્રક્રિયાનો ક્રમ.....View Solution
- 44$2A + B \rightarrow 3C + D$ પ્રક્રિયા માટે નીચેનામાંથી કયું એક પ્રક્રિયા દર આપતો નથી?View Solution
- 45$2A + B\rightarrow C$ પ્રક્રિયા માટે દર સમીકરણ દર $= k[A][B]$ છે. તો આ પ્રક્રિયાનાં સંબંધ માટે સાચું વિધાન કહો.View Solution
- 46$2A + B \rightarrow$ નિપજ પ્રક્રિયા માટે નીચેની કાર્યપદ્ધતિ આપેલ છે. તો પ્રક્રિયાનો ક્રમ ..... $2A $ $\rightleftharpoons$ $ A_2$ (ઝડપી) ; $A_2 + B \rightarrow P$ (ધીમી)View Solution
- 47$2N_2O_5(g) \rightarrow 4NO_2(g) + O_2(g)$ પ્રક્રિયા $N_2O_5 $ ના સંદર્ભમાં પ્રથમ ક્રમની છે તો નીચેનામાંથી કયો આલેખ સીધે રેખામાં મળે છે?View Solution
- 48$2N_2O_5(g) \rightarrow 4NO_2 (g) + O_2(g) $ પ્રથમ ક્રમની પ્રક્રિયા માટે કયું વિધાન ખોટું છે?View Solution
- 49$2N_2O_5 \rightarrow 4NO_2 + O_2 N_2O_5$ નું વિઘટન થાય છે અને પ્રથમ ક્રમ ગતિને અનુસરે છે. જેથી.View Solution
- 50$2N_2O_5 \rightarrow 4NO_2 + O_2$ પ્રક્રિયા માટે જો $NO_2$ ની સાંદ્રતા $1.6 × 10^{-2}$ સેકન્ડમાં વધે છે તો $ NO_2$ નો નિર્માણ દર.....View Solution
- 51$2NO_(g) + O_{2(g)} \rightarrow 2NO_{2(g)}$ પ્રક્રિયા પ્રણાલી માટે, કદ એ અચાનક ઘટીને અડધું થાય છે. જો પ્રક્રિયા એ પ્રથમ ક્રમની $O_2$ માટે અને દ્વિતીય ક્રમની $NO $ માટે હોય, તો પ્રક્રિયાનો દર.....View Solution
- 52$2O_3 \rightarrow 3O_2$ રાસાયણિક પ્રક્રિયા નીચે મુજબ દર્શાવી છે. તો દર નિયમ સમીકરણ..... થશે.View Solution
$ O_3 $ $\rightleftharpoons$ $ O_2 + O$ ...... (ઝડપી) ;
$O + O_3 \rightarrow 2O_2$ ...... (ધીમી)
- 53$2X + Y \rightarrow Z + W,$ પ્રાથમિક પ્રક્રિયા માટે આણ્વીયતા.....View Solution
- 54$300\, K$ તાપમાને નીચેની પ્રક્રિયાની સક્રિયકરણ ઊર્જા અને વેગ અચળાંક અનુકમે $10\, kJ\, mol^{-1}$ અને $2.4 \times 10^{-5}\, s^{-1}$ છે. તો ....... $K$ તાપમાને $t_{1/2}$ નું મૂલ્ય $2\, hr$ થશે.View Solution
$\mathop {2{N_2}{O_5}}\limits_{{\rm{(in}}\,\,{\rm{CC}}{{\rm{l}}_4}{\rm{)}}} \to \mathop {4N{O_2}}\limits_{{\rm{(in}}\,\,{\rm{CC}}{{\rm{l}}_4}{\rm{)}}} + {O_2}$
- 55$300\,^o C$ તાપમાને પ્રથમ કમની એક પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા $35\, kcal\, mol^{-1}$ અને આવૃત્તિ અવયવ $1.45 \times 10^{-11}\,s^{-1}$ છે, તો વેગ અચળાંક જણાવો.View Solution
- 56$320\,^o C$ તાપમાને પ્રથમ ક્રમની પ્રક્યિાView Solution
$S{{O}_{2}}C{{l}_{2}}\to S{{O}_{2}}+C{{l}_{2}}$ નો વેગ અચળાંક $2.2 \times 10^{-5}\, s^{-1}$ છે. આ વાયુને $90\, min$ સુધી ગરમ કરતા કેટલા $(\%)$ ટકા $SO_2Cl_2$ નુ વિધટન થશે ?
- 57$50\,mm$ $AB_3$ નું ઉદ્દીપકીય વિઘટન માટે અદ્ય આયુ સમય $4$ કલાક અને $100\,mm$ એ તેને $2$ કલાક લાગે છે તો પ્રક્રિયાનો ક્રમ..... થશે?View Solution
- 58$6{H^ + }\, + \,\,BrO_3^ - \, + \,\,5B{r^ - }\, \to \,\,3B{r_2}\, + \,\,3{H_2}O$ પ્રક્રિયા માટે નીચેનામાંથી કયો સંબંધ નિપજના વપરાશ અને નિર્માણ માટે સાચો છે?View Solution
- 59$A_2 + B_2 $ $\rightleftharpoons$ $ 2AB $ પુરોગામી અને પ્રતિવર્તીં પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા અનુક્રમે $180\, kJ$ મોલ $^{-1}$ અને $200 \,kJ$ મોલ $^{-1}$ છે. ઉદ્દીપકની હાજરીમાં (પુરોગામી અને પ્રતિવર્તીં) બંનેની સક્રિયકરણ ઊર્જા $100\, kJ$ મોલ $^{-1}$ ઘટે છે તો ઉદ્દીપકની હાજરીમાં ($A_2 + B_2 \rightarrow2AB$) પ્રક્રિયાનો એન્થાલ્પી ફેરફાર ( $kJ $ મોલ $ ^{-1}$) કેટલો થશે?View Solution
- 60$A + 2B\rightarrow $ નિપજ $ (P)$ પ્રક્રિયાનો દર નિયમ $\frac{{d[P]}}{{dt}}\,\, = \,\,K{[A]^2}[B]$ છે. જો મોટા પ્રમાણમાં $ [A]$ લેવામાં આવે તો પ્રક્રિયાનો ક્રમ શું થશે?View Solution
- 61$A + B\rightarrow C$ કાલ્પનીકે પ્રક્રિયા માટે ત્રણ જુદાંજુદાં પ્રયોગોમાં નીચેની માહિતી આપેલી છે.View Solution
$1$. $[A]$ $0.01$, $[B]$ $0.01 -$ પ્રક્રિયાનો દર $1.0 \times 10^{-4}$.
$2$. $[A]$ $0.01$, $[B]$ $0.03 - $ પ્રક્રિયાનો દર $9.0 \times 10^{-4}$.
$3$. $[A]$ $0.03$, $[B]$ $0.03 -$ પ્રક્રિયાનો દર $2.70\times 10^{-3}$ તો દર નિયમ સૂચવે કે...
- 62$A + B\rightarrow C$ નીચેની પ્રક્રિયા માટે દર્શાવેલ માહિતીને લાગુ પડતુ દર નિયમ પસંદ કરો.View Solution
$1$. $[A]$ $0.012$, $[B]$ $0.0351\rightarrow $ પ્રારંભિક દર $ = 0.10$
$2$. $[A]$ $0.024$, $[B]$ $0.070\rightarrow $ પ્રારંભિક દર $= 1.6$
$3$. $[A]$ $0.024$, $[B]$ $0.035\rightarrow $ પ્રારંભિક દર $ = 0.20$
$4$. $[A]$ $0.012$ , $[B]$ $0.070\rightarrow $ પ્રારંભિક દર $ = 0.80$
- 63$A + B \rightarrow$ નિપજો પ્રક્રિયા માટે $A$ ની સાંદ્રતા બમણી કરતા પ્રક્રિયા દર ચાર ગણી વધશે, પણ પરંતુ $B$ ની સાંદ્રતા બમણી કરતા પ્રક્રિયા દર પર અસર કરતું નથી. તો દર સમીકરણ ......View Solution
- 64$A + B \rightarrow $ નિપજ, પ્રક્રિયા માટે $A$ ના સંદર્ભમાં ક્રમ $1$ છે અને $B$ ના સંદર્ભમાં ક્રમ $1/2 $ છે. જ્યારે $A$ અને $B$ બંનેની સાંદ્રતા ચાર ગણી વધે છે. તો દર એ ....... ગુણાંક વધે છે.View Solution
- 65$A + B \rightarrow $ નિપજ, પ્રક્રિયા માટે પ્રક્રિયાનો દર બમણો થશે જ્યારે $A$ ની સાંદ્રતા બમણી થાય, તો દર ફરીથી બમણો થશે જ્યારે $A $ અને $ B$ ની સાંદ્રતા બમણી કરતા પ્રક્રિયાનો ક્રમ ...... થશે.View Solution
- 66$aG + bH \rightarrow$ નિપજ પ્રક્રિયાને ધ્યાનમાં લેતાં જ્યારે $G$ અને $H$ બંને પ્રક્રિયકોની સાંદ્રતા બમણી હોય તો દર વધીને $8$ ગણું થાય છે. જો કે જ્યારે $G$ ની સાંદ્રતા બમણી થાય ત્યારે $H$ ની સાંદ્રતા નિયત રહે તો દર બમણો થશે. તો સમગ્ર પ્રક્રિયાનો ક્રમ શું થશે?View Solution
- 67$A \rightarrow B$ પ્રથમ ક્રમની પ્રક્રિયા માટે $0.01\,M$ પ્રક્રિયકની સાંદ્રતાની પ્રક્રિયા દર $2.0 \times 10^{-5} $ મોલ $L^{-1}\,S^{-1} $ છે. તો પ્રક્રિયાનો અદ્ય આયુ ........ સેકન્ડ છે.View Solution
- 68$A \rightarrow P$ પ્રથમ ક્રમની પ્રક્રિયા માટે, તાપમાન $(T)$ આધારે દર અચળાંક $(k)$ નીચેના સમીકરણ $\log \,k = \, - (2000)\,\frac{1}{T}+ 0.6$ પર આધારિત છે. તો પૂર્વ ઘાતાંકીય ગુણાંક $A$ અને સક્રિયકરણ ઊર્જા $E_a$ અનુક્રમે... થાય.View Solution
- 69$A\rightarrow$ નિપજ ચોક્કસ પ્રક્રિયાનો અર્ધઆયુ સમય $1$ કલાક છે. જ્યારે પ્રક્રિયક $ 'A' $ ની શરૂઆતની સાંદ્રતા $2.0$ મોલ $L^{-1}$ હોય તો જો શૂન્ય ક્રમની પ્રક્રિયા હોય તો તેની સાંદ્રતા $0.50$ થી $0.25$ મોલ $L^{-1}$ સુધી આવતાં ......... $h$ લેશે.View Solution
- 70$C_2H_5I + OH \rightarrow C_2H_5OH + I^{-}$ પ્રક્રિયા માટે $30^o$ સે. અને $60^o$ સે. તાપમાને વેગ અચળાંકના મલ્યો અનુક્રમે $0.325$ અને $6.735$ લિટર મોલ$^{-1}$ સેકન્ડ $^{-1} $ હોય તો સક્રિયકરણ ઊર્જા $(E_a)$ નું મૂલ્ય .......... કેલરી થશે.View Solution
- 71$H_2 + I_2 \rightarrow 2HI $ પ્રક્રિયા માટે સાચો વિકલનીય વેગનિયમ જણાવો.View Solution
- 72$H_2 + I_2 $ $\rightleftharpoons$$H_I$ પ્રક્રિયા માટે સાચો સંબંધ લખો.View Solution
- 73$H_2O_2$ ના વિઘટનની પ્રક્રિયાનો વેગ અચળાંક $3.66 \times 10^{-3}\,s^{-1}$ છે. જો $H_2O_2$ ની શરૂઆતની સાંદ્રતા $0.882\, M$ હોય, તો ........ $\sec$ એ તેની સાંદ્રતા $0.600\,M$ થશે.View Solution
- 74$H_2O_2$ ના વિધટનથી $O_2$ ઉત્પન્ન થાય છે. જો કોઇ ચોક્કસ સમયે $1$ મિનિટમાં $48\,g$ $O_2$ ઉત્પન્ન થાય તો તે સમયે પાણીના ઉત્પાદનનો દર .......... $mol\, min^{-1}$ થશે.View Solution
- 75$KMnO_4$ સાથે હાઇડ્રોજન પેરોક્સાઇડના ઓક્સિડેશનનો વેગ અચળાંક $6.93 \times 10^{-5}\, s^{-1}$ છે. તો પ્રમાણિત $KMnO_4$ ના દ્રાવણનુ કદ $20\,mL$ થી $8\, mL$ થવા માટે કેટલો સમય લાગશે ?View Solution
- 76$Kt = lnC_0 - lnC_t$ સમીકરણમાં $ t$ અને $lnC_t$ વચ્ચેનો વક્ર ..... માં હોય.View Solution
- 77$(n - 1)$ ક્રમની પ્રક્રિયા માટે અર્ધપ્રક્રિયા સમય અને શરૂઆતની સાંદ્રતા વચ્ચેનો સંબધ કયો છે?View Solution
- 78$N_2 + 3H_2 \rightarrow 2NH_3$ પ્રક્રિયા માટે જો $\frac{{ - d\,[N{H_3}]}}{{dt}}\,\, = \,\,2\, \times \,{10^{ - 4}}$ મોલ.લિટર $^{-1}$.સેકન્ડ $^{-1}$ હોય, તો $\frac{{ - d\,[{H_2}]}}{{dt}}$ નું મૂલ્ય કેટલું થશે?View Solution
- 79$N_{2(g)} + 3H_{2(g)} \rightarrow 2NH_{3(g)}$ પ્રક્રિયા તાપમાનની ચોક્કસ પરિસ્થિતિ અને પ્રક્રિયકોનું આંશિક દબાણ હેઠળ થાય છે. $ NH_3$ નો નિર્માણ દર $ 0.001\,\,kg\, h^{-1}$ છે. તો $H_2$ નો રૂપાંતરણ દર તેજ સમાન પરિસ્થિતિમાં......$kg \,h^{-1}$ છે.View Solution
- 80$N_2O_5$ ના વિઘટનની પ્રક્રિયા માટે $\log\, K \to 1/T$ ના આલેખનો ઢાળ $-1.2 \times 10^4\,K$ મળે છે. તો પ્રક્રિયાની સક્રિયકરણ ઊર્જા જણાવો.View Solution
- 81$NaOH$ દ્વારા થતી સાબુની એસ્ટરીકરણ પ્રક્રિયાનો તાપમાન ગુણાંક $1.75$ છે. તો પ્રકિયાની સક્રિયકરણ ઊર્જા .......... $kcal\,mo{l^{ - 1}}$ થશે.View Solution
- 82$ N_2 + 3H_2\rightarrow 2NH_3 $ હેબર પ્રક્રિયા દ્વારા એમોનીયાના નિર્માણ માટે ભાગ લેતી ઉદ્દીપકીય પ્રક્રિયામાં $ NH_3 $ નો પારદર્શક દર $ 2.5 \times 10^{-4 } $ મોલ $L^{-1 }\,S^{-1 }$ છે તો $N_2$ નો અપારદર્શક દર કેટલો થશે?View Solution
- 83$n^{th}$ ક્રમની પ્રક્રિયા માટે વેગ નિયમ $x/dt = K [A]^n$ છે. તો લોગેરીધમ આલેખ પરથી ગતિનો કયું પદ મેળવી (તારવી) શકાય ?View Solution
- 84$t_{1/2}$ અને $ n^{th}$ ક્રમની પ્રક્રિયા માટે સાંદ્રતા વિરૂદ્ધ સમય નો આલેખ સીધી રેખામાં છે. જ્યારે સાંદ્રતા $2$ મોલ $L^{-1}$ હોય ત્યારે આ પ્રક્રિયાને $50\%$ પૂર્ણ થવા $10$ મિનિટ લાગે છે. આ પ્રક્રિયા $4$ મોલ $L^{-1}$ એ $t$ સમયમાં $50\%$ વિઘટન થાય તો $n$ અને $t$ અનુક્રમે.....View Solution
- 85$T\,K$ તાપમાને એક પ્રક્રિયાનો વેગ અચળાંક એ $2\,T$ તાપમાને પ્રકિયાના વેગ અચળાંક કરતા $10$ માં ભાગનો છે, તો આ પ્રક્રિયાની સક્રિયકરણ ઊર્જા કેટલી થશે ?View Solution
- 86$X$ અને $Y$ વચ્ચેની ચોક્કસ વાયુમય પ્રક્રિયામાં $X + 3Y \rightarrow XY_3$ તો પ્રારંભિક દર નીચે મુજબ દર્શાવાય.View Solution
$[X]$ $0.1\,M$, $[Y]$ $0.1\,M$ દર $\rightarrow 0.002\,Ms^{-1}$
$[X]$ $0.2\,M$, $[Y]$ $0.1\,M$ દર $\rightarrow 0.002\,Ms^{-1}$
$[X]$ $0.3\,M$, $[Y]$ $0.2\,M$ દર $\rightarrow 0.008\,Ms^{-1}$
$[X]$ $0.4\,M$, $[Y]$ $0.3\,M$ દર $\rightarrow 0.018\,Ms^{-1}$
તો દર નિયમ ......
- 87અહીં પ્રથમ ક્રમ પ્રક્રિયા માટે તેના $1\,M$ થી $0.6 \,M$ સુધી તેને $20$ મિનિટ લાગે છે. તો $0.6 \,M$ થી $0.36\, M$ સાંદ્રતા સુધી પહોચતા કેટલો સમય જરૂરી છે.View Solution
- 88આપેલ $T$ તાપમાને કેટલીક પ્રક્રિયાનો કેટલાક ક્રમ માટેનો દર અચળાંક $K$ છે તો $\mathop {\lim }\limits_{T \to \infty } \,\,\log \,\,K$...... મૂલ્ય મળશે.View Solution
- 89આપેલ પ્રક્રિયા માટે $'a'$ ની જુદીજુદી પ્રારંભિક સાંદ્રતા એ $t_{1/2}$ ની માહિતીનો ક્રમ જુદોજુદો હોય છે. જે $[t_{1/2}\,\alpha \,a] $ અચળ હશે તો પ્રક્રિયાનો ક્રમ ....... હશે.View Solution
- 90આર્ગોનની હાજરીમાં $N_2O$ નુ $N_2$ અને $O_2$ માં વિઘટન પ્રથમ કમની ગતિકીને અનુસરે છે. $K = 5.0 \times10^{11}\,e^{-2000/T}$ હોય તો પ્રકીયા સક્રિયકરણ ઊર્જા થશે?View Solution
- 91ઉષ્માક્ષેપક પ્રક્રિયા $A\rightarrow B$ ની સક્રિયકરણ ઊર્જા $15\,\,K\,cal/mol$ છે અને પ્રક્રિયાની ઉષ્મા $5 \,\,K\,cal/mol$ છે. તો $B \rightarrow A $ પ્રક્રિયા માટેની સક્રિયકરણ ઊર્જા ......... $K\,cal/mol$ થશે.View Solution
- 92ઉષ્માક્ષેપક પ્રક્રિયા $A \rightarrow B$ માટે $A$ ની સક્રીયકરણ ઊર્જા $17\, kJ$ પ્રતિ મોલ છે. પ્રક્રિયાની ઉષ્મા $40 \,kJ$ છે. તો પ્રતિવર્તીં પ્રક્રિયા $B \rightarrow A$ માટેની સક્રીયકરણ ઊર્જા ગણો.View Solution
- 93ઉષ્માક્ષેપક પ્રક્રિયા $X \rightarrow Y$ ની સક્રીયકરણ ઊર્જા $30\,KJ$ મોલ $^{-1}$ છે. જો પ્રક્રિયા દરમિયાન એન્થાલ્પી ફેરફાર $ ( \Delta H) - 20\, KJ$ છે, તો પ્રતિવર્તીં પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા...... $kJ$View Solution
- 94એક પદાર્થ $S$ સમાન પ્રક્રિયા પરિસ્થિતિમાં બે પ્રક્રિયા અનુભવે છેView Solution
$\mathop S\limits_{{\text{(2}}{\text{.0}}\,{\text{M)}}} \xrightarrow{{{K_0}}}X$ (zero order)
$\mathop S\limits_{{\text{(2}}{\text{.0}}\,{\text{M)}}} \xrightarrow{{{K_2}}}Y$ (second order)
શૂન્ય કમ અને દ્વિતીય ક્રમની પ્રક્રિયા મુજબ $S$ ની સાંદ્રતા અડધી થવા માટે અનુક્રમે $40\, s$ અને $10\, s$ લાગે છે. તો $K_0 / K_2$ ગુણોતરનું મૂલ્ય શુ થશે ?
- 95એક પ્રક્રિયાની સક્રિયકરણ ઊર્જા $94.14\, kJ\, mol^{-1}$ અને $310\, K$ તાપમાને વેગ અચળાંક મૂલ્ય $10^{-2}$ $s^{-1}$ છે. તો આવૃત્તિ અવયવ કેટલો થશે ?View Solution
- 96એક પ્રથમ ક્રમની પ્રક્રિયાને $90\%$ પૂર્ણ થવા લાગતો સમય આશરે ......... હોય છે.View Solution
- 97એક વાયરૂપ પ્રક્રિયાનો વેગ $r = K\,[x]\, [y]$ છે. જો એકાએક પાત્રનુ કદ ઘટાડીને શરૂઆતના કદથી $1/4$ જેટલુ કરવામાં આવે તો પ્રક્યિાનો વેગ ............View Solution
- 98એસ્ટરનુ જળવિભાજન મંદ એસિડ $A$ અને $B$ દ્વારા ઉદ્દીપિત થાય છે. બંને પ્રક્રિયાઓ માટે વેગ અચળાંક અનુક્રમે $K_A$ અને $K_B$ છે. જો $K_A > K_B$ હોય તો નીચેનામાંથી ક્યુ વિધાન સાચું છે ?View Solution
- 99ઓઝોનને ગરમ કરવાથી તેનુ ઓક્સિજનમાં નીચે મુજબ વિધટન થાય છે.View Solution
${O_3} \rightleftharpoons {O_2} + \left[ O \right]$
${O_3} + \left[ O \right] \to 2{O_2}$ (slow)
તો $2{O_3} \to 3{O_2}$ પ્રક્રિયાનો કમ જણાવો.
- 100ઓરડાના તાપમાને $NO$ અને $O_2$વચ્ચે પ્રક્રિયા થઈ $NO_2$ મળે જે ઝડપી થાય છે. જ્યારે $CO $ અને $O_2$ વચ્ચે પ્રક્રિયા ધીમી થાય કારણ કે.....View Solution