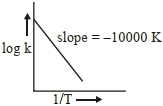Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1પ્રથમ ક્રમ પ્રક્રિયામાં $a/(a - x) 10$ મિનિટ પછી $8$ મળે છે તો દર અચળાંક શું થશે?View Solution
- 2પ્રથમ, દ્વિતીય અને તૃતીય ક્રમના ત્રણ પ્રક્રિયા માટેના દર અચળાંક આંકડામાં સમાન હોય છે. પ્રક્રિયકની સાંદ્રતા સમાન અને $1\,M$ કરતા વધારે હોય તો આ ત્રણ પ્રક્રિયાનો દર માટે ગતિમાં કયું એક સાચું છે?View Solution
- 3View Solutionપ્રદિપ્તીનુ બુઝાવુ ........ પર આધાર રાખે છે.
- 4પ્રારંભિક પ્રકિયા $2AB + B \to A_2B_3$ એ પ્રકિયકોના સમાન મોલ લઇને $1\, dm^3$ અને $2\, dm^3$ કદના પાત્રોમાં અલગ રીતે કરવામાં આવે તો પ્રક્રિયાવેગનો ગુણોત્તર $(r_1/r_2$) ...View Solution
- 5બંધ પાત્રમાં $2N_2O_5(g) $ $\rightleftharpoons$ $ 4NO_2(g) + O_2(g)$ નો અભ્યાસ કરતાં $NO_2$ ની સાંદ્રતા પાંચ સેકન્ડમાં $2.0 × 10^{-2} mol L^{-1}$ વધે છે. તો $N_2O_5$ ની સાંદ્રતા ફેરફારનો દર ગણો.View Solution
- 6બંધ પાત્રમાં $2N_2O_5(g) $ $\rightleftharpoons$ $ 4NO_2(g) + O_2(g)$ નો અભ્યાસ કરતાં $NO_2$ ની સાંદ્રતા પાંચ સેકન્ડમાં $2.0 \times 10^{-2} \,mol \,L^{-1}$ વધે છે. તો પ્રક્રિયાનો દર.....View Solution
- 7બે પ્રક્રિયાઓ માટે પૂર્વઘાતાંક અવયવના મૂલ્યો સમાન છે.પરંતુ તેમની સક્રિયકરણ ઊર્જાતા મૂલ્યો વચ્ચે $24.9\, kJ\,mol^{-1}$ તો $300\, K$ તાપમાને તેમના વેગ અચળાંકોનો ગુણોત્તર ....View Solution
- 8મોટા ભાગની પ્રક્રિયાનો તાપમાન ગુણાંક $.......$ ની વચ્ચે હોય છે.View Solution
- 9રાસાયણિક પ્રક્રિયા $2A + 2B + C \rightarrow$ નિપજ માટે સમીકરણને અનુસરતા : $r \propto [A] [B]^2$ પ્રક્રિયાનો ક્રમ......View Solution
- 10રાસાયણિક પ્રક્રિયા નીચે આપેલ તબક્કામાંથી પસાર થાય છે.View Solution
તબક્કો $: I :$ $2A $ $\rightleftharpoons$ $ X $ ઝડપી.
તબક્કો $II :$ $X + B $ $\rightleftharpoons$ $Y$ ધીમી
તબક્કો $III :$ $Y + B$ નીપજ ઝડપી આખી પ્રક્રિયા કયા નિયમ પર આધારિત છે ?
- 11રાસાયણિક પ્રક્રિયાને ધ્યાનમાં લેતાં : $N_2(g) + 3H_2(g) \rightarrow 2NH_3(g)$ આ પ્રક્રિયાનો દર તેના $N_2(g), H_2(g)$ અથવા $NH_3(g) $ ની સાંદ્રતાના સમયના સંદર્ભના સમજાવી શકાય છે તો આ દર સમીકરણ વચ્ચેનો સાચો સંબંધ શોધો.View Solution
- 12રેડિયોએક્ટિવ ક્ષયમાં એક યુરેનિયમ પરમાણુનુ એક લેડ પરમાણુમાં રૂપાંતર થાય છે. જો ચંદ્ર પરના એક ખડકના નમૂનામાં યુરેનિયમ તથા લેડના પરમાણુઓની સંખ્યા સમાન હોય તથા યુરેનિયમ માટે $t_{1/2} = 4.5 \times 10^9$ વર્ષ હોય તો ખડકનુ આયુષ્ય .... થશે. છેView Solution
- 13રેડીયોએક્ટિવ સમસ્થાનીકનું અર્ધઆયુ ત્રણ કલાક છે. જો સમસ્થાનિકનું શરૂઆતનું દળ $256\, g$ હોય તો $18$ કલાક પછી કેટલા $g$ દળ બાકી રહેશે?View Solution
- 14રેડીયો સમસ્થાનિકની અર્ધઆયુ ચાર કલાક છે. જો સમસ્થાનિકનું શરૂઆતનું દળ $200\,g$ હોય તો $24$ કલાક પછી ....... $g$ દળ બાકી રહેશે.View Solution
- 15રેડીયો સમસ્થાનીક ટ્રીટીયમ $(_1^3H)$ નો અદ્ય આયુ સમય $12.3$ વર્ષ છે. જો ટ્રીટીયમનું પ્રારંભિક મુલ્ય $32\,mg,$ હોય તો $49.2$ વર્ષ પછી કેટલા મીલીગ્રામ બાકી રહેશે ?View Solution
- 16વાતાવરણના ઉપરના સ્તરમાં ઓઝોન વિઘટન નાઇટ્રિક ઓક્સાઇડ દ્વારા ઉદ્દીપિત થાય છે. પ્રક્રિયાની ક્રિયાવિધિ નીચે મુજબ છે.View Solution
$2NO \rightleftharpoons {N_2}O + \left[ O \right]$
${O_3} + \left[ O \right] \to 2{O_2}\,(slow)$
તો પ્રકિયાનો કમ જણાવો.
- 17વાયુમય પ્રક્રિયા માટે, દર $= k [A] [B].$ જો પાત્રનું કદ ઘટીને $1/4$ પ્રારંભિક થશે તો પ્રક્રિયાનો દર પ્રારંભિક સમયમાં....... થશે.View Solution
- 18વાયુરૂપ ઘટકો વચ્ચેની પ્રક્રિયા : $2A + B\rightarrow C + D. $ માટે પ્રક્રિયા વેગ $= K[A][B] $ છે. તો પહેલા કરતા પાત્રનું $1/4$ કદ જેટલુ ઓછુ લેવામાં આવે તો પહેલાના પ્રક્રિયા વેગ કરતાં અંતિમ પ્રક્રિયા વેગ કેટલા ગણો મળશે ?View Solution
- 19વાયુરૂપ પ્રક્યિા ${A_{\left( g \right)}} \to 2{B_{\left( g \right)}} + {C_{\left( g \right)}}$ પ્રથમ ક્રમની પ્રક્રિયા છે. જો પ્રક્રિયાની શરૂઆતમાં $P_A = 90\, mm\, Hg$ હોય અને $10\, min$ બાદ કુલ દબાણ $180\, mm\, Hg$ જણાય, તો પ્રક્રિયાનો વેગઅચળાંક જણાવો.View Solution
- 20શૂન્ય કમની પ્રક્રિયાનો વેગ અચળાંક $0.2\, mol\,L^{-1}\, hr^{-1}$ છે. જો અડધા કલાક પછી પ્રક્રિયકની સાંદ્રતા $0.05\, M$ હોય, તો પ્રક્રિયકની શરૂઆતની સાંદ્રતા ....... $M$ થશે.View Solution
- 21શૂન્યકમની પ્રક્રિયા માટે $t_{1/2}$ અને $t_{3/4}$ નો ગુણોત્તર .... થશે.View Solution
- 22View Solutionશૂન્યક્રમની પ્રક્રિયા માટે કયો વિકલ્પ યોગ્ય છે ?
- 23શૂન્ય ક્રમ પ્રક્રિયાનો દર અચળાંક $0.2 $ મોલ $m^{-3}\,h^{-1}$ છે. જો પ્રક્રિયકની સાંદ્રતા $30$ મિનિટ પછી $0.05 $ મોલ $m^{-3}$ હોય તો તેની પ્રારંભિક સાંદ્રતા ....... મોલ $ m^{-3}$ થશે.View Solution
- 24શૂન્ય ક્રમ પ્રક્રિયા માટે $K= 2 \times 10^{-2}$ મોલ $L^{-1}$ સેકન્ડ $^{-1}$ છે. જો $25$ સેકન્ડ પછી પ્રક્રિયકની સાંદ્રતા $0.5\,M$ થાય તો તેની પ્રારંભિક સાંદ્રતા ...... $M$ હોવી જોઈએ.View Solution
- 25સમાન પ્રક્રિયાની પરિસ્થિતિ હેઠળ પદાર્થની સાંદ્રતા $1.386$ મોલ $m^{-3}$ છે. જે $40$ સેકન્ડમાં અને $20$ સેકન્ડમાં પ્રથમ ક્રમ અને શૂન્ય ક્રમ ગતિ દ્વારા અડધી થશે. પ્રથમ ક્રમ $(k_1)$ અને શૂન્ય ક્રમ $(k_0)$ માટેનો દર અચળાંકનો ગુણોત્તર $\left( {\frac{{{k_1}}}{{{k_0}}}} \right)$ ............ $mol^{-1}\,dm^3$ થશે.View Solution
- 26સમીકરણ $2{N_2}{O_5}_{\left( g \right)} \to 4N{O_{2\left( g \right)}} + {O_{2\left( g \right)}}$ મુજબ ${N_2}{O_5}$ નુ વિઘટન એ પ્રથમ કમની પ્રક્રિયા છે. બંધ પાત્રમાં પ્રક્રિયાની શરૂઆત થયા બાદ $30\, \min$ ના અંતે કુલ દબાણ $305.5\, mm\, Hg$ હોય અને સંપૂર્ણ વિઘટનના અંતે કુલ દબાણ $587.5\, mm\, Hg$ જણાય, તો પ્રક્રિયાનો વેગઅચળાંક જણાવો.View Solution
- 27સંસ્પર્શ પ્રક્રિયા દ્વારા $ 2SO_2 (g) + O_2(g) \rightarrow 2SO_3(g)$ સલ્ફર ટ્રાયોક્સાઈડનાં નિર્માણમાં તે પ્રક્રિયાનો દર $-\frac{d({{O}_{2}})}{dt}=2.5\times {{10}^{-4}}\,mol\text{ }{{L}^{-1}}{{\sec }^{-1}}$ છે. તો તેના $(SO_2) $ નો અપારદર્શક દર કેટલો થશે?View Solution
- 28$2 \mathrm{~A}+\mathrm{B} \rightarrow \mathrm{C}+\mathrm{D}$ પ્રક્રિયા ના ગતિકીય અભ્યાસ દરમિયાન, નીચે મુજબ ના પરિણામો પ્રાપ્ત થયા.View Solution
$A[M]$ $B[M]$ સર્જન નો પ્રારંભિક વેગ $D$
$i$ $0.1$ $0.1$ $6.0 \times 10^{-3}$ $ii$ $0.3$ $0.2$ $7.2 \times 10^{-2}$ $ii$ $0.3$ $0.4$ $2.88 \times 10^{-1}$ $iv$ $0.4$ $0.1$ $2.40 \times 10^{-2}$ ઉપ૨ની માહિતી ના આધારે સમગ્ર પ્રક્રિયાનો ક્રમ ........ છે.
- 29અચળ તાપમાન પ૨ વાયુ અવસ્થામાં નીચે આપેલ એક તબક્કીય પ્રક્રિયા ને ધ્યાનમાં લો.View Solution
$2 \mathrm{~A}_{(\mathrm{g})}+\mathrm{B}_{(\mathrm{g})} \rightarrow \mathrm{C}_{(\mathrm{g})}$
જ્યારે પ્રક્રિયા, $A$ નું $1.5 \mathrm{~atm}$ દબાણ અને $\mathrm{B}$ નાં $0.7 \mathrm{~atm}$ દબાણ સાથે પ્રારંભ (શરૂ) કરવામાં આવ્યો હોય ત્યારે પ્રક્રિયાનો પ્રારંભિક વેગ $r_1$ તરીક નોંધવામાં આવ્યો. થોડાક સમય પછી, જ્યારે $C$ નું દબાણ $0.5 \mathrm{~atm}$ થાય છે ત્યારે $r_2$ વેગ નોંધવામા આવ્યો, $r_1: r_2$ ગુણોત્તર ............ $\times 10^{-1}$ છે.
(નજીક નો પૂર્ણાક)
- 30અચળ તાપમાન પર નીચે આપેલી પ્રથમ ક્રમ વાયુઅવસ્થા પ્રક્રિયાને ધ્યાનમાં લો.View Solution
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$23 \mathrm\ {sec}$ પછી જો વાયુઆનું કુલ દબાણ $200\ torr$ મળી આવેલ હોય અને ખુબજ લાંબા સમય બાદ $A$ નાં સંપૂર્ણ વિધટન પર $300\ torr$ મળી આવેલ હોય તો આપેલ પ્રક્રિયા નો વેગ અચળાંક ......... $\times 10^{-2} \mathrm{~s}^{-1}$ છે. [આપેલ : $\left.\log _{10}(2)=0.301\right]$
- 31એક પ્રક્રિયા $\mathrm{A} \xrightarrow{\mathrm{K}_4} \mathrm{~B} \xrightarrow{\mathrm{K}_2} \mathrm{C}$ માટે , જો $B$ ના સર્જન ( નિર્માણ) નો વેગ શૂન્ય સેટ કરવામાં આવે તો ($B$) ની સાંદ્રતા આપવામાં આવે છે :View Solution
- 32એક પ્રથમ ક્રમ પ્રક્રિયા માં $99.9\%$ પૂર્ણ થવા માટેનો જરૂરી સમય એ $90 \%$ પ્રક્રિયા પૂર્ણ થવા માટેના જરૂરી સમય કરતાં .......... ગણો છે.View Solution
- 33નીચે આપેલ પ્રક્રિયાને ધ્યાનમાં લો.View Solution
$\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}$
$A$ ની પ્રારંભિક સાંદ્રતા થી $1 / 4^{\text {th }}$ થવા માટે લાગતો સમય એજ પ્રક્રિયામાં $1 / 2$ થવા માટેના લાગતા સમય કરતા બમણો છે. જ્યારે $B$ ની સાંદ્રતામાં ફેરફાર વિરુદ્ધ સમયની આલેખ દોરવામાં આવે તો, પરિણામી આલેખ ઋણ ઢાળ સાથે સીધી રેખા અને સાંદ્રતા અક્ષ પર ધન આંતછેદ આપે છે. સમગ્ર પ્રક્રિયાનો ક્રમ ............ છે.
- 34નીચે આપેલ બે જુદી જુદી પ્રથમ ક્રમ પ્રક્રિયા ને ધ્યાનમાં લોView Solution
$\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}$ (પ્રક્રિયા $1)$
$\mathrm{P} \rightarrow \mathrm{Q}$ (પ્રક્રિયા $2$)
પ્રક્રિયા $1$ : પ્રક્રિયા $2$ ના અર્ધં આયુષ્ય નો ગુણોત્તર $5: 2$ છે. પ્રક્રિયા $1$ અને પ્રક્રિયા $2$ ને $2 / 3^{\text {dd }}$ and $4 / 5^{\text {dd }}$ પૂર્ણ થવા માટે લાગતા સમયને અનુક્રમે $t_1$ અને $t_2$ તરીકે રજૂ કરવા આવે તો $t_1: t_2$ ગુણોત્તર નું મૂલ્ય ........... $\times 10^{-1}$ છે. (નજીક નો પૂર્ણાક)
[આપેલ : $\log _{10}(3)=0.477$ અને $\log _{10}(5)=0.699$ ]
- 35નીચે આપેલા પ્રકિયા ને ધ્યાન માં લો, વેગ અભિવ્યક્તિ કે જે નીચે આપેલ છે.View Solution
$\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}$
$\text { rate }=\mathrm{k}[\mathrm{A}]^{1 / 2}[\mathrm{~B}]^{1 / 2}$
$A$ અને $B$ એમ દરેક ની સાદ્રતા $1 M$ લઇ ને પ્રક્રિયા શરૂ કરવામાં આવે છે. જો વેગ અયળાંક ($k$) એ $4.6 \times 10^{-2} \mathrm{~s}^{-1}$, હોય તો $A$ ને $0.1 \mathrm{M}$ થવા માટે જરૂરી સમય .................. sec છે. (નજીક નો પૂર્ણાંક)
- 36નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.View Solution
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
સ્ટેપ Rate constant $\left(\sec ^{-1}\right)$
Activation energy
$\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
$1$ ${k}_1$ $300$ $2$ ${k}_2$ $200$ $3$ ${k}_3$ $\mathrm{Ea}_3$ ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).
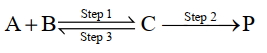
- 37નીચે બે વિધાન આપેલા છે :View Solution
વિધાન $I$ : $A+B \rightarrow C$ પ્રક્રિયા માટે વેગ નિયમ, વેગ $(r)=k[A]^2[B]$ છે. જ્યારે $A$ અને $B$ એમ બંને ની સાંદ્રતા બમણી કરવામાં આવે છે ત્યારે પ્રક્રિયા વેગ વધી ને " $x$ " ગણો થાય છે.
વિધાન $II$ :
(Image)
આકૃતિ " " $y$ " ક્રમ પ્રક્રિયા માટે સાંદ્રતામાં તફ઼ાવત સામે સમયનો આલેખ દર્શાંવે છે. $x+y$ નું મૂલ્ય . . . . . છે.
- 38$2 \mathrm{~N}_2 \mathrm{O}_{5(\mathrm{~g})} \rightarrow 4 \mathrm{NO}_{2(\mathrm{~g})}+\mathrm{O}_{2(\mathrm{~g})}$ સમીકરણ વડે $\mathrm{CCl}_4$ માં $\mathrm{N}_2 \mathrm{O}_5$ ની વિઘટન થઈને પ્રકિયા માટે જરૂરી $\mathrm{NO}_2$ ઉત્પન્ન થાય છે. $\mathrm{N}_2 \mathrm{O}_5$ ની પ્રારંભિક સાંદ્રતા $3 \mathrm{~mol} \mathrm{~L}^{-1}$ અને તેની $30$ મિનીટ પછી $2.75 \mathrm{~mol} \mathrm{~L}^{-1}$ છે. $\mathrm{NO}_2$ બનવાનો (સર્જન) વેગ (દર) એ $x \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}$ છે. $x$ નું મુલ્ય___________ છે.(નજીકનો પૂણાંક)View Solution
- 39અચળ ક્દે વાયુ $A$ નાં પ્રથમ ક્રમના ઉષ્મીય વિઘટન દરમિયાન નીચે મુજબ માહિતી પ્રાપ્ત થાય છે.View Solution
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$S.\ No$ સમય/s કુલ દબાણ/(atm)
$1.$ $0$ $0.1$
$2.$ $115$ $0.28$
પ્રક્રિયાનો વેગ અચળાંક _______________$\times 10^{-2} \mathrm{~s}^{-1}$ (નજીકનાં પૂનાંકમાં)
- 40આપેલ પ્રક્રિયા માટે નીચે આપેલ માહિતીને ધ્યાનમાં લો.View Solution
$2 \mathrm{HI}_{(\mathrm{g})} \rightarrow \mathrm{H}_{2(\mathrm{~g})}+\mathrm{I}_{2(\mathrm{~g})}$
પ્રક્રિયાનો ક્રમ................ છે.
$1$ $2$ $3$ $\mathrm{HI}\left(\mathrm{mol} \mathrm{L}^{-1}\right)$ $0.005$ $0.01$ $0.02$ Rate $\left(\mathrm{mol} \mathrm{L}^{-1} \mathrm{~s}-1\right)$ $7.5 \times 10^{-4}$ $3.0 \times 10^{-3}$ $1.2 \times 10^{-2}$ - 41એક પ્રથમ ક્રમની પ્રક્રિયાના $99.9\%$ પૂર્ણ થવા માટેનો જરૂરી સમય એ પ્રક્રિયાના અર્ધ આયુષ્ય $\left(\mathrm{t}_{1 / 2}\right)$ ના____________ સમય જેટલો છે.View Solution
- 42પ્રક્રિયા માટે $\mathrm{r}=\mathrm{k}[\mathrm{A}]$ આપેલ છે, જો $\mathrm{A}$ નું $50\%$ વિઘટન $120$ મિનીટમાં થાય તો $90 \%$ વિઘટન માટે કેટલો સમય લાગશે.View Solution
- 43પ્રથમ ક્રમની વાયુમય પ્રક્રિયા માટે સંકલીત વેગ નિયમ ક્યા સમીકરણથી દર્શાવી શકાય છે. (જ્યાં $P_i=$ પ્રારંભિક દબાણ, $\mathrm{P}_{\mathrm{t}}=\mathrm{t}$ સમયે કુલ દબાણ)View Solution
- 44પ્રથમ ક્રમ પ્રક્રિયાનો વેગ પ્રક્રિયાની શરૂઆત થયા પછી $10$ minutes પર $0.04 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~S}^{-1}$ છે અને $20 \ minutes$ પર $0.03 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}$ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય _______________ $minutes$ છે. (આપેલ : $\log 2=0.3010, \log 3=0.4771)$View Solution
- 45રેડિયો સમસ્થાનિક બ્રોમિન - $82$ નો અર્ધ-આયુષ્ય $36$ hours છે. એક દિવસ પછી બાકી રહતો અંશ (ભાગ)_______$\times 10^{-2}$છે.(આપેલ એન્ટીલોગ (પ્રતિલઘુગુગક) $0.2006 = 1.587$)View Solution
- 46લાકડા ના એક ટૂકડામાં $\frac{{ }^{14} \mathrm{C}}{{ }^{12} \mathrm{C}}$ નો ગુણોત્તર, વાતાવરણ ની તુલના માં $\frac{1}{8}$ મો ભાગ છે. જો ${ }^{14} \mathrm{C}$ નો અર્ધ આયુષ્ય $5730$ વર્ષ હોય તો, લાકડાના નમૂનાની ઉંમર (આયુ)___________ છે.View Solution
- 47સમાન તાપમાન પર એક પ્રક્રિયા ત્રણ તબકકકાઓમાં થાય છે. સમગ્ર વેગ અચળાંક $K=\frac{K_1 K_2}{K_3}$ છે. જો $\mathrm{Ea}_1, \mathrm{Ea}_2$ અને $Еаз$ એં અનુક્મે $40,50$ અને $60 \mathrm{~kJ} / \mathrm{mol}$ હોય તો, સમગ્ર Ea $\mathrm{kJ} / \mathrm{mol}$છે.View Solution
- 48$87.5 \%$ પ્રક્રિયા પૂર્ણ થવા માટે જરૂરી સમય $t_{87.5}$ છે અને $50 \%$ પ્રક્રિયા પૂર્ણ થવા માટે જરૂરી સમય $t _{50}$ છે. $t _{87.5}=x \times t _{50}$ સંબંધ ધરાવે છે.તો $x$ નું મૂલ્ય $........$ છે.View Solution
- 49$A ( g ) \rightarrow 2 B ( g )+ C ( g )$ એ એક પ્રથમ પ્રક્રિયા છે.પ્રણાલિક નું પ્રારંભિક દબાણ $800\,mm$ $Hg$ મળેલ છે કે જે $10\,min$ પછી $1600\,mm\,Hg$ સુધી વધે છે.$30\,min$ પછી પ્રણાલી નું કુલ દબાણ $.....\,mm\,Hg$ થશે.(નજીકનો પૂર્ણાક)View Solution
- 50$A \rightarrow B$View Solution
$200\,K$ અને $300\,K$ પર ઉપરની પ્રક્રિયાના વેગ અચળાંકો અનુક્રમે $0.03\,min ^{-1}$ અને $0.05\,min ^{-1}$ છે. પ્રક્રિયા માટેની સક્રિયકરણ શકિત $.........J$ છે. (નજીકનો પૂર્ણાંક)
(આપેલ : In $10=2.3$
$R =8.3\,J\,K ^{-1}\, mol ^{-1}$
$\log 5=0.70$
$\log 3=0.48$
$\log 2=0.30$
- 51$A \rightarrow B$View Solution
ઉપરની પ્રક્રિયા શૂન્યક્રમની છે.આ પ્રક્રિયાને અર્ધ-આયુષ્ય $50\,min$ છે.$A$ની સાંદ્રતાને તેના શરૂઆતના મૂલ્યથી $\frac{1}{4}$ ઘટાડવા માટે લાગતો સમય $............\,min$ છે.(નજીકનો પૂર્ણાક)
- 52એક અણુ બે સ્વતંત્ર પ્રથમ ક્રમ પ્રક્રિયાઓ દર્શાવે છે કે જેના અર્ધ આયુષ્ય અનુક્રમે $12\,min$ અને $3\,min$ છે. જો બન્ને પ્રક્રિયાઓ થાય તો પછી પ્રક્રિયકના $50 \%$ વાપરવા માટે લેવાતો (જરૂરી) સમય $.......\,\min$ છે.(નજીકનો પૂર્ણાક)View Solution
- 53એક ઉત્સેચક ઉદ્દીપકીય પ્રક્રિયાના વેગ સાથે ક્રિયાધાર (અવસ્તર) સાંદ્રતાની બદલાવ આલેખ વડે પ્રદર્શિત કરે છે તે $..............$View Solution
- 54View Solutionધનાત્મક ઉદ્દીપક પ્રક્રિયા માટે સાચી પ્રક્રિયા પ્રોફાઈલ આલેખ (ડાયાગ્રામ) શોધો.
- 55પક્રિયા $2 NO + Br _2 \rightarrow 2 NOBr$View Solution
નીચે આપેલ પ્રક્કિયાવિધી દ્વારા થઈ રહી છે.
$NO + Br _2 \Leftrightarrow NOBr _2 \text { (fast) }$
$NOBr _2+ NO \rightarrow 2 NOBr$(ધીમી)
પ્રક્રિયાનો સમગ્ર ક્રમ $........$
- 56પ્રથમક્રમની પ્રક્રિયાને અનુસરીને એક સંયોજન $A$,સંયોજન $B$ સાથે પ્રક્રિયા કરે છે, જેનો વેગ અચળાંક $2,011 \times 10^{-3}\,s^{-1}$ છે.સંયોજન $A$ ના $7\,g$ ને $28$ માં ઘટતા લાગતો સમય (સેકન્ડોમાં) $.....$ છે.(નજીકનો પૂર્ણાક) $[\log 5=0.698, \log 7=0.845, \log 2=0.301]$View Solution
- 57પ્લેટીનમ ઉપર હાઇડ્રોજન ના અધિશોષણ માટે, સક્રિયકરણ શક્તિ $30\,kJ\,mol ^{-1}$ છે અને નિકલ ઉપર હાઈડ્રોજનના અધિશોષણ માટે, સક્રિયકરણ શક્તિ $41.4\,kJ\,mol ^{-1}$ છે.$300\,K$ પર ધાતુઓના સમાન વિસ્તારો ઉપર રસાયણિક અધિશોષણ ના વેગ ના લધુગુણક નો ગુણોતર $.....$ છે.(નજીક નો પૂર્ણાક) [આપેલ $\left.\ln 10=2.3 \quad R =8.3\,J\,K ^{-1}\,mol ^{-1}\right]$View Solution
- 58રસાયણિક પ્રક્રિયા $A+B \rightarrow$ નીપજ માટે,$A$ અને $B$ ના સંદર્ભ સાથે ક્રમ $1$ છેView Solution
Rate $mol\,L^{-1}\,s^{-1}$ $[A]$ $mol\,L^{-1}$ $[B]$ $mol\,L^{-1}$ $0.10$ $20$ $0.5$ $0.40$ $x$ $0.5$ $0.80$ $40$ $y$ $x$ અને $y$ ના મુલ્યો શું છે ?
- 59સંયોજન $A \rightarrow B$ ના પરિવર્તન માટે,પ્રક્રિયાનો વેગ અચળાંક $4.6 \times 10^{-5}\,L\,mol ^{-1}\,s ^{-1}$ માલૂમ પડેલ છે. તો પ્રક્રિયાનો ક્રમ $.............$ છે.View Solution
- 60$25 ^{\circ}\,C$ પર એક વાયુ $AB _3$ ના વિધટનનો અભ્યાસ એક વિદ્યાર્થીએ કર્યો તેને નીચે મુજબની માહિતી મેળવી.View Solution
$p ( mm Hg )$ $50$ $100$ $200$ $400$ સાપેક્ષ $t _{1 / 2}( s )$ $4$ $2$ $1$ $0.5$ પ્રક્રિયાનો ક્રમ શોધો.
- 61$KClO _3+6 FeSO _4+3 H _2 SO _4 \rightarrow KCl +3 Fe _2\left( SO _4\right)_3+3 H _2 O$View Solution
ઉપરોક્ત પ્રક્રિયાનો અભ્યાસ $FeSO _4$ ની સાંદ્રતાનું નિરીક્ષણ કરીને $300\,K$ પર કરવામાં આવ્યો હતો, જેમાં પ્રારંભિક સાંદ્રતા $10\,M$ હતી અને અડધા કલાક પછી $8.8\,M$ થઈ ગઈ હતી. $Fe _2\left( SO _4\right)_3$ ના ઉત્પાદનનો વેગ એ $..........\,\times 10^{-6}\,mol\,L ^{-1}\,s ^{-1}$ છે.
- 62એક કાર્બનિક પદાર્થનું પ્રથમ ક્રમ હેઠળ વિધટન થાય છે. $60 \%$ વિધટન માટે લાગતો સમય $90 \%$ હોય તો, $540\,s$ વિઘટન માટે જરૂરી સમય $..........s$ હશે.(નજીકનો પૂર્ણાંક)(આપેલ : $\ln 10=2.3 ; \log 2=0.3$ )View Solution
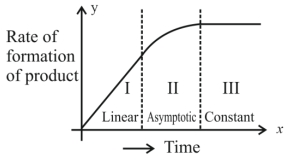
- 63એક નિશ્ચિત રાસાયણિક પ્રક્રિયા $X \rightarrow Y$ માટે, નીપજના બનવાનો દર વિરુદ્ધ સમયનો ગ્રાફ (આલેખ) એ આકૃતિમાં દર્શાવેલ છે. નીચે આપેલામાંથી સાચાં વિધાન/નોની સંખ્યા $..............$ છે.View Solution
$(A)$ સમગ્ર પ્રક્રિયાનો ક્રમ છે.
$(B)$ આ પ્રક્રિયાનો ક્રમ શોધી શકાતો નથી.
$(C)$ $I$ અને $III$ વિભાગ માં, પ્રક્રિયા અનુક્રમે પ્રથમ અને શૂન્ય ક્રમની છે.
$(D)$ વિભાગ $II$ માં, પ્રક્રિયા પ્રથમક્રમની છે.
$(E)$ વિભાગ $II$ માં, પ્રક્રિયાનો ક્રમ $0.1$ થી $0.9$ વિસ્તાર માં છે.
- 64એક પ્રથમક્રમ પ્રક્રિયા $A \rightarrow B$ માટે, અર્ધ આયુષ્ય $30\,min$ છે. $75\%$ પ્રક્રિયા પૂર્ણ માટે લાગતો સમય $.............\,min$ છે.(નજીકનો પૂર્ણાંક)View Solution
આપેલ : $\log 2=0.3010,\log 3=0.4771,\log 5=0.6989$
- 65એક પ્રથમ ક્રમ પ્રક્રિયા એ વેગ અયળાંક $k =4.6 \times 10^{-3}\,s ^{-1}$ ધરાવે છે. નીચે આપેલામાંથી સાચાં વિધાન/નો ની સંખ્યા $.............$ છે.આપેલ: $\log 3=0.48$View Solution
$A.$ $1000\,s$ માં પ્રક્રિયા પૂર્ણ થાય છે.
$B.$ પ્રક્રિયા $500\,s$ નો અર્ધ-આયુષ્ય ધરાવે છે.
$C.$ $90 \%$ પૂર્ણ થવા માટેનો લાગતો જરૂરી સમય કરતાં $10 \%$ પૂર્ણ થવા માટે નો જરૂરી સમય $25$ ગણો છે.
$D.$ વિયોજન અંશ એ (1- $\left.e ^{-k t}\right)$ ને સમાન છે.
$E.$ વેગ (દર) અને વેગ અચળાંક (દર અચળાંક) સમાન એકમ ધરાવે છે.
- 66એક પ્રથમ ક્રમ પ્રક્રિયા માટે વેગ અચળાંક $20\,min ^{-1}$ છે. પ્રક્રિયકની પ્રારંભિક સાંદ્રતા તેના $\frac{1}{32}$ સ્તર સુધી ધટાડવા માટે લાગતો જરૂરી સમય $..........\times 10^{-2}\,min$ છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલ : $\ln 10=2.303\,\log 2=0.3010$ )
- 67નીચે આપેલ વિધાન/નો ની સંખ્યા કે જે સાચા છે તે $......$View Solution
$A$.વેગ અચળાંક નો તાપમાન પર આધાર પ્રબળ, સક્રિયકરણ શક્તિ (ઊર્જા) ઊચી હોય છે
$B$.જો પ્રક્રિયા શૂન્ય સક્રિકરણ શક્તિ ધરાવે, તો તેનો વેગ તાપમાન થી સ્વતંત્ર છે
$C$.વેગ અચળાંક નો તાપમાન પર આધાર પ્રબળ, સક્રિયકરણ શક્તિ (ઊર્જા) નીચી હોય છે
$D$.જો તાપમાન અને વેગ અયળાંક વચ્ય જો સહસંબંધ ના હોય તો પછી તેનો ઈ અર્થ થાય છે કે પ્રક્રિયા ઋણ સક્રિયકરણ શક્તિ ધરાવે છે.
- 68નીચે આપેલામાંથી ખોટા વિધાન/નો ની સંખ્યા $........$ છે.View Solution
$A$. શૂન્ય ક્રમની પ્રક્રિયાઆના અનુગામી અર્ધ આયુષ્ય સમય સાથે ધટે છે.
$B$. રાસાયણિક સમીકરણ પ્રક્રિયક તરીકે દેખાતો પદાર્થ પ્રક્રિયાના (પ્રક્રિયાવેગને)દરને અસર કરી શકે નહી.
$C$. એક રાસાયણિક પ્રક્રિયાની આણિવક્તા અને ક્રમ અપૂર્ણાક સંખ્યા હોઈ શકે છે.
$D$. શૂન્ય અને દ્વિતિય ક્રમ પ્રક્રિયાનો વેગ અચળાંક અનુક્રમે $mol\,L ^{-1}\,s ^{-1}$ અને $mol ^{-1}\,L$ $s^{-1}$ છે.
- 69$2 NO +2 H _{2} \rightarrow N _{2}+2 H _{2} O$View Solution
ઉપરોક્ત પ્રક્રિયાનો અભ્યાસ $800^{\circ} C$ એ કરવામાં આવ્યો. યોગ્ય માહિતી નીચેના કોષ્ટકમાં આપેલી છે.
Run $H2$ નું પ્રારંભિક દબાણ / $kPa$ $NO$ નું પ્રારંભેક દબાણ / $kPa$ પ્રારંભિક વેગ $\left(\frac{- dp }{ dt }\right) /( kPa / s )$ $1$ $65.6$ $40.0$ $0.135$ $2$ $65.6$ $20.1$ $0.033$ $3$ $38.6$ $65.6$ $0.214$ $4$ $19.2$ $65.6$ $0.106$ $NO$ ના સંદર્ભે પ્રક્રિયાનો ક્રમ ......... છે
- 70$30^{\circ} C$ પર, $AB _2$ ના વિધટનનો અર્ધ આયુષ્ય $200 \,s$ છે અને જે $AB _2$ ના પ્રારંભિક સાંદ્રતાથી સ્વતંત્ર છે. તો $80\, \% AB _2$ ના વિઘટન માટેના સમયની સીમા શોધો. ($s$ માં)View Solution
(આપેલ : $\log 2=0.30, \log 3=0.48$ )
- 71$345\,K$ પર, $55.5\,kPa$ પર શરૂઆતમાં એક વાયુમય સંયોજનના નમૂનાના વિધટન માટે તેની અર્ધ આાયુષ્ય $340\,s$ માલૂમ પડયો. જ્યારે દબાણ $27.8\,kPa$, હોય ત્યારે અર્ધ આયુષ્ય $170\,s$ માલૂમ પડયું. પ્રક્રિયાનો ક્રમ$\dots\dots\dots$છે.(નજીકનો પૂર્ણાંક)View Solution
- 72$700 -$ $1000\,K$ તાપમાન શ્રેણીમાં (વિસ્તાર માં) એસિટાલ્ડીહાઈડના વિઘટન માટેના દર (વેગ) અચળાંક માપવામાં આવ્યાં. $\ln k$ વિરુદ્ધ $\frac{10^{3}}{ T }$ આલેખ દોરીને માહિતીનું પૃથ્થકરણ કરવામાં આવ્યું.પ્રક્રિયા માટે સક્રિયકરણ શક્તિનું મૂલ્ય $\dots\dots\dots$$kJ\,mol { }^{-1}$ છે.(નજીકનો પૂર્ણાંક)View Solution
(આપેલ:$R =8.31\,JK ^{-1}\,mol ^{-1}$)
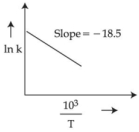
- 73$A \rightarrow 2 B + C$ પ્રક્રિયા માટે જ્યારે પ્રક્રિયક $A$ ની સાંદ્રતા અનુક્રમે $0.5$ અને $1.0\, mol \,L ^{-1}$ હોય ત્યારે તેમના અર્ધઆયુુષ્યો અનુક્રમે $100\, s$ અને $50\, s$ થાય છે. પ્રક્રિયાનો ક્રમ $....$ છે.View Solution
- 74$[ A ]$ પ્રક્રિયક $\rightarrow$ $[ B ]$ નીપજView Solution
જો સંયોજન $[B]$નું બનવું એ પ્રથમક્રમ ગતિકીને અનુસરતું હોય તો, અને $70 \,mins$ પછી $[A]$ ની સાંદ્રતા તેની પ્રારંભિક સાંદ્રતા કરતા અડધી મળી આવેલ છે. પ્રક્રિયાનો વેગ અચળાંક એ $x \times 10^{-6}\, s ^{-1}$ છે. તો $x$ નું મૂલ્ય નજીકના પૂર્ણાંકમાં $.....$ છે.
- 75$X$ અને $Y$ વચ્ચેની પ્રક્રિયા $X$ ના સાપેક્ષમાં પ્રથમ ક્રમ અને $Y$ ના સાપેક્ષમાં શૂન્ય ક્રમ ની છે.View Solution
પ્રયોગ $\frac{[ X ]}{ mol \;L ^{-1}}$ $\frac{[ Y ]}{ mol\; L ^{-1}}$ $\frac{\text { Initial rate }}{ mol\; L ^{-1}\; min ^{-1}}$ $I$ $0.1$ $0.1$ $2 \times 10^{-3}$ $II$ $.2$ $0.2$ $4 \times 10^{-3}$ $III$ $0.4$ $0.4$ $M \times 10^{-3}$ $IV$ $0.1$ $0.2$ $2 \times 10^{-3}$ $M$ મૂલ્યનો સંખ્યાત્મક ગુણોત્તર $........$ છે. (નજીકનો પૂર્ણાંક)
- 76આપેલ રાસાયણિક પ્રક્રિયા માટે,View Solution
$\gamma_{1} A +\gamma_{2} B \rightarrow \gamma_{3} C +\gamma_{4} D$
જ્યાં $v_{1}, v_{2}, v_{3}$ અને $v_{4}$ એ પૂર્ણાંક છે. $(i.e.$ $\left.1,2,3,4 \ldots . .\right)$
$10$ સેકન્ડોના અંતરાલ માં $C$ ની સાંદ્રતા $10\,m\,mol\,dm ^{-3}$ માંથી $20\,m\,mol\,dm ^{-3}$ માં ફેરફાર થાય છે.$D$નો દશ્ય થવાનો વેગ એ $B$ના અદશ્ય થવાના વેગ કરતા $1.5$ ગણો છે, ને $A$ ના અદશ્ય થવાના વેગ કરતા બમણો છે.પ્રાયોગિક રીતે $D$ના દશ્ય થવાનો વેગ $9,m\,mol\,dm ^{-3} \,s ^{-1}$ શોધવામાં આવ્યો.તેથી પ્રક્રિયાનો વેગ $\dots\dots\,\,m\,mol$$dm ^{-3} s ^{-1}.$
- 77આરંભમાં જયારે વાયુનું દબાણ $500 \,torr$ હોય ત્યારે વાયુમય સંયોજન $A$ નો વિધટન માટે અર્ધઆયુષ્ય $240\, s$ છે. જ્યારે દબાણ $250 \,torr$ હોય ત્યારે અર્ધ આયુષ્ય $4.0 \,min$ મળે છે. તો પ્રક્રિયાક્રમ $........$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
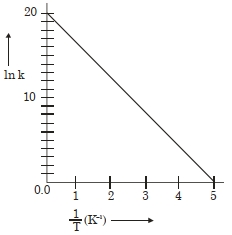
- 78એક પ્રક્રિયા માટે, $\ln K$ વિરુદ્ધ $\frac{1}{ T }$ નો આલેખ નીચે આપેલો છે. પ્રક્રિયાની સક્રિયકરણ ઊર્જા $......cal$ $mol ^{-1}$ (નજીકના પૂર્ણાંક)View Solution
(આપેલું છે: $R =2\,cal\,K ^{-1}\,mol ^{-1}$ )
- 79એક ફ્લાસ્કમાં પ્રક્રિયા ન કરતાં હોય તેવા $A$ અને $B$ ના સમાન (એક સરખા) $moles$ ભરવામાં આવેલ છે.$A$ અને $B$નું અર્ધ-આયુષ્ય અનુક્રમે $100\,s$ અને $50\,s$ છે અને તે પ્રારંભિક (શરૂઆત) સાંદ્રતા થી સ્વતંત્ર છે.$A$ની સાંદ્રતા $B$નાં કરતા ચાર ઘણી થાય તે માટેનો જરૂરી સમય. $\dots\dots\dots\,s$ છે.View Solution
(આપેલ : $\ln 2=0.693)$
- 80એક રાસાયણિક પ્રક્રિયાનો વેગ અચળાંક, પ્રક્રિયાના તાપમાનમાં $9\, K$નો વધારો કરતા બમણો માલૂમ પડયો.જો પ્રક્રિયા $300\, K$ તાપમાને થતી હોય તેમ ધારીએ તો, સક્રિયકરણ ઊર્જાનુ મૂલ્ય............$k\,J\, mol ^{-1}$ થાય. [નજીકનો પૂર્ણાંક]View Solution
(આપેલું છે$: \ln 10=2.3, R =8.3 \,J\, K ^{-1} \,mol ^{-1}, \log 2=0.30$ )
- 81એક રેડિયોએક્ટિવ તત્વનો અર્ધ આયુષ્ય $200 \,days$ (દિવસો) છે. $83 \,days$ (દિવસો) પછી બાકી રહેલ મૂળ સક્રિયતાની ટકાવારી $.....$ છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલ : એન્ટીલોગ $antilog$ $0.125=1.333$,
$\text { antilog } 0.693=4.93 \text { ) }$
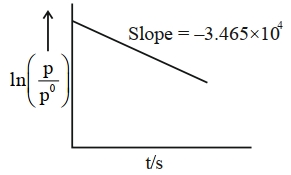
- 82એઝોમિથેનના વિધટન માટે,View Solution
$CH _3 N _2 CH _3( g ) \rightarrow CH _3 CH _3( g )+ N _2( g )$
આ એક પ્રથમક્રમ પ્રક્રિયા છે. $600\, K$ પર સમય સાથે આંશિક દબાણમાં વિવિધતા નીચે આપેલ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય $\times 10^{-5}\, s$ છે. [નજીકનો પૂર્ણાંક]
- 83ધારીલો કે, $1\,\mu\,g$ ઓછા પ્રમાણમાં રેડિયો એકિટવ તત્ત્વ $ X$ કે જેનું અર્ધ આાયુષ્ય $30$ વર્ષ છે,જે ઉગતા વૃક્ષમાં અવશોષણ પામે છે. તો $100$ વર્ષ બાદ $X$ની માત્રા જે વૃક્ષમાં રહેશે તે $......\times 10^{-1}\,\mu\,g$ માં શોધો.[આપેલ: $\ln 10=2.303 ; \log 2=0.30]$View Solution
- 84પ્રથમ ક્રમની એક પ્રક્રિયાની વેગ અચળાંક નીચેના સમીકરણ દ્વારા આપેલ છે.View Solution
$\ln k=33.24-\frac{2.0 \times 10^{4} \,K }{ T }$
તે પ્રક્રિયાની સક્રિયકરણ ઊર્જા $.....\,kJ\, mol ^{-1}$ થશે. (નજીકનો પૂર્ણાંકમાં)
(આપેલ છે : $R =8.3 \,J \,K ^{-1} \,mol ^{-1}$ )
- 85પ્રથમ ક્રમની પ્રક્રિયા $A → B$ માટે દર અયળાંક $k =5.5 \times 10^{-14} s ^{-1} .67 \%$ પૂર્ણ થવા માટેનો જરૂરી સમય તેના પ્રક્રિયાના અર્ધ આયુષ્ય કરતા $x \times 10^{-1}$ ગણો છે. તો $x$ નું મૂલ્ય $\dots\dots$છે.View Solution
- 86પ્રથમ ક્રમની પ્રક્રિયા માટે,$90\%$ પ્રક્રિયા પૂર્ણ થવા માટે લાગતો સમય, પ્રક્રિયાના અર્ધ આયુષ્ય કરતા ' $x$ ' ગણો છે. તો ' $x$ નું મૂલ્ય શોધો. (આપેલ: $\ln 10=2.303$ અને $\log 2=0.3010$ )View Solution
- 87$k =\left(6.5 \times 10^{12} \,s ^{-1}\right) e ^{-26000 K / T }$ને ધ્યાનમાં લો.જો આ પ્રક્રિયાસંયોજન $A$ના વિઘટન માટે અનુસરવામાં આવે છે.સક્રિયકરણ શક્તિ આ પ્રક્રિયા માટે $\dots\dots\dots\,\,kJ\,mol^{-1}$[નજીકના પૂર્ણાંકમાં] (આપેલ: $R =8.314 \,J\, K ^{-1}\, mol ^{-1}$ )View Solution
- 88આપેલ પ્રથમક્રમ પ્રક્રિપા માટે $A \rightarrow B$ પ્રક્રિયાનો અર્ધ આયુષ્ય $0.3010 \,min$ છે. $2.0$ મિનીટના સમયે પ્રક્રિયિકી પ્રારંભિક (શરૂઆત) સાંદ્રતા થી પ્રક્રિયકનની સાંદ્રતાનો ગુણોત્તર ........ હશે.View Solution
- 89ઉદ્દીપક $A \,\,300\,\,K$ એ સક્રિયકરણ શક્તિ $10\,\,kJ\,\,mol ^{-1}$ જેટલી ધટાડે છે. પ્રક્રિયા દરનો ગુણોતર $\frac{ k _{ T }, \text { Catalysed }}{ k _{ T }, \text { Uncatalysed }}$ એ $e ^{ x }$ છે.$x$ નું મૂલ્ય $\dots\dots\dots$.[નજીકના પૂર્ણાંકમાં] [ધારી લો કે, પૂર્વ ધાતાકીય અવયવ બંને કિસ્સામાં સરખો છે. આપેલ $R =8.31 J K ^{-1} mol^{-1}$]View Solution
- 90એક જૈવરાસાયણિક પ્રક્રમમાં એક પ્રક્રિયાની સક્રિયકરણ શક્તિ $532611\,J\,mol ^{-1}$ છે. જયારે તાપમાન $310\,K$ થી $300\,K$ માં ઓછું થાય ત્યારે જોવા મળતો વેગ અચળાંકમાં ફેફાર $k _{300}=x \times 10^{-3}\,k _{310}$ તો $x$ નું મૂલ્ય $.....$ છે.View Solution
[આપેલ: $\ln 10=2.3$$R =8.3\, J \, K ^{-1}\, mol ^{-1}$]
- 91$27^{\circ} C$ થી $52^{\circ} C$ તાપમાનમાં વધારો કરતાં એક પ્રક્રિયાનો વેગ અચળાંક પાંચ ગણો વધે છે. તો સક્રિયકરણ શક્તિ નું મૂલ્ય $kJ mol ^{-1}$ માં ....... છે.View Solution
(નજીકનાં પૂર્ણાકમાં રાઉન્ડ ઑફ) $\left[ R =8.314\, J \,K ^{-1} \,mol ^{-1}\right]$
- 92$2 NO ( g )+ Cl _{2}( g ) \rightleftharpoons 2 NOCl ( s )$View Solution
આ પ્રક્રિયાનો $-10^{\circ} C$ પર અભ્યાસ કરાયો હતો અને નીચેની માહિતી મળી હતી.
ક્રમ $[ NO ]_{0}$ $\left[ Cl _{2}\right]_{0}$ $r _{0}$ $1$ $0.10$ $0.10$ $0.18$ $2$ $0.10$ $0.20$ $0.35$ $3$ $0.20$ $0.20$ $1.40$ $[ NO ]_{0}$ અને $\left[ Cl _{2}\right]_{0}$ શરૂઆતની સાંદ્રતા અને $r _{0}$ શરૂઆતનો પ્રક્રિયાનો વેગ છે, તો પ્રક્રિયાનો ક્રમ શું હશે?
- 93$700\, {~K}$ પર ${CaCO}_{3}$ના વિયોજન માટે પ્રથમ ક્રમનો દર અચળાંક $6.36 \times 10^{-3}\, {~s}^{-1}$ અને સક્રિયકરણ ઊર્જા $209\, {~kJ} \,{~mol}^{-1}$ છે. તેનો $500\, {~K}$ પર દર અચળાંક (${s}^{-1}$ માં) ${x} \times 10^{-6}$ છે. ${x}$નું મૂલ્ય $.....$ છે.(નજીકના પૂર્ણાંકમાં)View Solution
$[$આપેલ છે :${R}=8.31\, {~J} \,{~K}^{-1} \,{~mol}^{-1} ; \log 6.36 \times 10^{-3}=-2.19$ $\left.10^{-4.79}=1.62 \times 10^{-5}\right]$
- 94$975\, {~K}$ પર નીચે આપેલ રાસાયણિક પ્રક્રિયા માટે નીચેની માહિતી મેળવવામાં આવ્યો હતો.View Solution
$2 {NO}_{({g})}+2 {H}_{2({~g})} \rightarrow {N}_{2({~g})}+2 {H}_{2} {O}_{({g})}$
$[NO]$
${mol} {L}^{-1}$
${H}_{2}$
${mol} {L}^{-1}$
વેગ
${mol}L^{-1}$ $s^{-1}$
$(A)$ $8 \times 10^{-5}$ $8 \times 10^{-5}$ $7 \times 10^{-9}$ $(B)$ $24 \times 10^{-5}$ $8 \times 10^{-5}$ $2.1 \times 10^{-8}$ $(C)$ $24 \times 10^{-5}$ $32 \times 10^{-5}$ $8.4 \times 10^{-8}$ ${NO}$ના સંદર્ભમાં પ્રક્રિયાનો ક્રમ $....$ છે.
- 95$A \rightarrow B$ રાસાયણિક પ્રક્રિયા માટે, એવું જાણવા મળ્યું કે $B$ ની સાંદ્રતા $0.2\, mol\,L^{-1}$ $30\, {~min}$માં વધી છે. પ્રક્રિયાનો સરેરાશ વેગ $......\times 10^{-1} {~mol} {~L}^{-1} {~h}^{-1}$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
- 96$A$ અને $B$ પ્રથમ ક્રમ ગતિકી વડે વિઘટન પામે છે જેનો અર્ધ-આયુષ્ય અનુક્રમે $54.0\, min$ અને $18.0\, min$ છે. $A$ અને $B$ નાં અ-સક્રિય મિશ્રણમાં (જે માં પ્રક્રિયા ના થતી હોય તેવું મિશ્રણ) સમ મોલર થી શરૂઆત કરીએ તો, $A$ ની સાંદ્રતાં $B$ નાં કરતાં $16$ ગણી વધારે રહે તે માટેનો લાગતો સમય $..... \, min.$ છે. (નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઓફ કરો)View Solution
- 97${N}_{2} {O}_{5(9)} \rightarrow 2 {NO}_{2(9)}+\frac{1}{2} {O}_{2({~g})}$View Solution
ઉપરોક્ત પ્રથમ ક્રમની પ્રક્રિયામાં $318 \,K$ પર ${N}_{2} {O}_{5}$ની પ્રારંભિક સાંદ્રતા $2.40 \times 10^{-2}\, {~mol} \,{~L}^{-1}$ છે. $1$ કલાક પછી ${N}_{2} {O}_{5}$ની સાંદ્રતા $1.60 \times 10^{-2}\, {~mol} \,{~L}^{-1}$ હતી. $318\, {~K}$ પર પ્રક્રિયાનો વેગ અચળાંક $.....\,\times 10^{-3} {~min}^{-1}.$ (નજીકના પૂર્ણાંકમાં)
[આપેલ છે: $\log 3=0.477, \log 5=0.699$ ]
- 98ચોક્કસ પ્રથમ ક્રમની પ્રક્રિયા માટે $570 \,s$ પછી $32 \%$ પ્રક્રિયક બાકી રહે છે. આ પ્રક્રિયાનો વેગ અચળાંક ........... $\times 10^{-3} s ^{-1}$ છે.View Solution
$\left[\right.$ આપેલ છે $\left.: \log _{10} 2=0.301, \ln 10=2.303\right]$
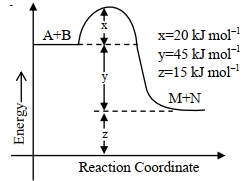
- 99નીચેના આંકડા મુજબ, પ્રક્રિયાના એન્થાલ્પી ફેરફારની તીવ્રતાView Solution
${A}+{B} \rightarrow {M}+{N}$ $......$ ${kJ} {mol}^{-1}$ બરાબર છે. (નજીકના પૂર્ણાંકમાં)
- 100પ્રક્રિયા, $a A +b B \rightarrow c C +d D$ માટે, આલેખ $\log \,k$ વિરૂધ્ધ $\frac{1}{ T }$ ને નીચે આપેલ છેView Solution
કયા તાપમાને $(K$ માં) પ્રક્રિયાનો વેગ અચળાંક $10^{-4} s ^{-1}$ થશે તે શોધો ?(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ)
[આપેલ : $500\, K$ પર, પ્રક્રિયાનો વેગ અચળાંક $10^{-5} s^{-1}$ છે.]