$0.12\; m $ લંબાઇ અને $0.1\; m$ પહોળાઇની તથા $50$ આંટાવાળી લંબચોરસ કોઇલને $0.2\;Wb/m^2$ ના સમાન નિયમિત ચુંબકીયક્ષેત્રમાં ઊર્ધ્વ દિશામાં લટકાવેલી છે. કોઇલમાંથી $ 2\,A$ નો પ્રવાહ વહે છે. જો ગૂંચળાનું સમતલ ચુંબકીય ક્ષેત્રની દિશા સાથે $30^o $ નો ખૂણો બનાવે, તો કોઇલને સ્થાયી સમતોલનમાં રાખવા માટે કેટલા ટોર્કની ($N-m$ માં) જરૂર પડે?
AIPMT 2015, Medium
c
The required torque is \(\tau=N I A B \sin \theta\)
The required torque is \(\tau=N I A B \sin \theta\)
where \(N\) is the number of turns in the coil, \(I\) is the current through the coil, \(B\) is the uniform magnetic field, \(A\) is the area of the coil and \(\theta\) is the angle between the direction of the magnetic field and nomal to the plane of the coil. Here, \(N=50, I=2\, \mathrm{A},\)
\(A=0.12\, \mathrm{m} \times 0.1\, \mathrm{m}=0.012\, \mathrm{m}^{2}\)
\(B=0.2\, \mathrm{Wb} / \mathrm{m}^{2} \text { and } \theta=90^{\circ}-30^{\circ}=60^{\circ}\)
\(\therefore \quad \tau =(50)(2\, \mathrm{A})\left(0.012\, \mathrm{m}^{2}\right)\left(0.2\, \mathrm{Wb} / \mathrm{m}^{2}\right) \sin 60^{\circ} \)
\(=0.20\, \mathrm{N} \mathrm{m}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઇલેક્ટ્રોન બીમ પરસ્પર લંબ વિદ્યુત અને ચુંબકીય ક્ષેત્રો માંથી વિચલન વગર ગતિ કરે છે. જો વિદ્યુત ક્ષેત્ર બંધ કરી દેવામાં આવે અને ચુંબકીય ક્ષેત્ર યથાવત રાખવામાં આવે, તો ઈલેક્ટ્રોન કેવી ગતિ કરે?
- 2$I$ પ્રવાહ ધરાવતી એક વર્તુળાકાર લૂપની દ્વિદ્યુવી ચાકમાત્રા $m$ છે.અને લૂપના કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર $B_1$ જેટલું છે.જયારે પ્રવાહ અચળ રાખીને દ્વિદ્યુવી ચાકમાત્રા બમણી કરવામાં આવે છે,ત્યારે લૂપના કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર $B_2$ થાય છે. $\frac{{{B_1}}}{{{B_2}}}$ ગુણોત્તર ______.View Solution
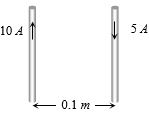
- 3આપેલ આકૃતિમાં રહેલા બે તાર વચ્ચે કેટલું બળ લાગશે? [${\mu _0} = 4\pi \times {10^{ - 7}}$ $weber/amp -m]$View Solution
- 4$25\,\Omega $ અવરોધ ધરાવતા ગેલ્વેનોમીટરના પૂર્ણ આવર્તન માટે $1\,mA$ પ્રવાહની જરૂર પડે છે. $2\,A$ પ્રવાહનું આવર્તન દર્શાવે તેવો એમીટર બનાવવા માટે તેની સાથે કેટલા મૂલ્યનો શંટ અવરોધ જોડાવો પડે?View Solution
- 5બે સમાંતર રહેલા પ્રવાહધારિત તાર વચ્ચેનું અંતર $b$ છે.તો એક તાર દ્વારા બીજા તારના એકમ લંબાઇ દીઠ કેટલું બળ લાગશે?View Solution
- 6$4 \,cm$ ત્રિજયા અને $50$ આંટા ધરાવતી કોઇલમાં $2 \,A$ પ્રવાહ પસાર કરીને $0.1\, weber/{m^2} $ ના ચુંબકીયક્ષેત્રમાં મૂકેલી છે.સમતોલન સ્થિતિમાંથી $ 180^\circ $ ના ખૂણે ફેરવવા કેટલા .......$J$ કાર્ય કરવું પડે?View Solution
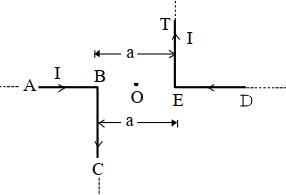
- 7આકૃતિમાં દર્શાવેલ વીજપ્રવાહની ગોઠવણી માટે $O$ બિંદુએ ચુંબકીય પ્રેરણનું મૂલ્યView Solution
- 8અચળ વેગ સાથે ગતિ કરતો પ્રોટોન અવકાશના વિસ્તારમાંથી તેના વેગમાં ફેરફાર થયા વગર, પસાર થાય છે. જો $E$ અને $B$ નીચેનામાંથી ક્યું હોઈ શકે ?View Solution
- 9કોઈ એક ક્ષેત્રમાં સ્થિત વિદ્યુતક્ષેત્ર અને ચુંબકીયક્ષેત્ર પ્રવર્તે છે.ચુંબકીયક્ષેત્ર $\vec B = {B_0}\left( {\hat i + 2\hat j - 4\hat k} \right)$ મુજબ આપવામાં આવે છે. જો એક વિજભાર આ ક્ષેત્રમાં $\vec v = {v_0}\left( {3\hat i - \hat j + 2\hat k} \right)$ ના વેગથી ગતિ કરતો હોય ત્યારે કોઈ બળ અનુભવતો ના હોય તો $SI$ એકમમાં વિદ્યુતક્ષેત્ર કેટલું હશે?View Solution
- 10એક $L$ મીટર લંબાઇ અને $I$ એમ્પિયર પ્રવાહધારીતા તારને વર્તુળાકાર રીતે વાળવામાં આવે તો ચુંબકીય મોમેન્ટ ........... મળેView Solution
