$0.3\;cm$ અને $20\;cm$ ત્રિજ્યા ધરાવતી વર્તુળાકાર લૂપને સમઅક્ષીય એકબીજાને સમાંતર $15\;cm$ અંતરે મૂકેલી છે. જો નાની લૂપમાં પ્રવાહ $20\,A$ પસાર કરતાં મોટી લૂપ સાથે સંકળાયેલ ચુંબકીય ફલકસ ..... .
AIIMS 2018, Medium
a
Magnetic flux linked with bigger circular loop is given by
Magnetic flux linked with bigger circular loop is given by
\(\phi=\frac{\mu_{0}}{2} \cdot \frac{\pi I R_{1}^{2} R_{2}^{2}}{\left(R_{1}^{2}+x^{2}\right)^{3 / 2}}\)
Putting the values,
\(\phi=\frac{4 \pi \times 10^{-7} \times \pi \times 15 \times\left(0.3 \times 10^{-2}\right)^{2} \times\left(20 \times 10^{-2}\right)^{2}}{\left[\left(0.3 \times 10^{-2}\right)^{2}+\left(15 \times 10^{-2}\right)^{2}\right]^{3 / 2}}\)
By solving, we get
\(\phi=9.116 \times 10^{-11} Wb\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$8.4 \,mH$ ઇન્ડકટન્સ અને $6\,Ω$ અવરોઘ ઘરાવતી કોઇલને $12\, V$ સાથે જોડેલ છે. કોઇલમાં $1 \,A$ પ્રવાહ કેટલા સમય પછી પસાર થશે?View Solution
- 2View Solutionકેટલાક ગેલ્વેનોમીટરોના સ્થિત સળિયા અચુંબકીય ધાત્વિય પદાર્થમાંથી બનાવવામાં આવેલા છે. ધાત્વિય પદાર્થનું કાર્ય છે.
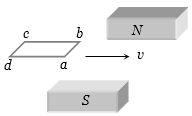
- 3લૂપ $abcd$, $t=0$ સમયે અચળ વેગ $ v$ થી ચુંબક વચ્ચે દાખલ થાય છે,તો ઉદ્ભવતા $emf$ $(e)$ વિરુધ્ધ સમય $(t)$ નો આલેખ કેવો થાય?View Solution
- 4View Solutionચુંબકીય ફ્લક્સનું પારિમાણિક સૂત્ર શું થાય?
- 5$5\,Ω$ અવરોધ અને $20\,H$ ઇન્ડકટન્સને બેટરી સાથે જોડતાં પ્રવાહ $4\, A/sec$ ના દરથી વધે છે,તો બેટરીનો વોલ્ટેજ કેટલા .....$V$ થાય?View Solution
- 6ચુંબકને કોઇલ તરફ $(i)$ ઝડપી અને $(ii)$ ધીમેથી ગતિ કરાવતાં ઉત્પન્ન થતું $emf$ અને વિદ્યુતભાર અનુક્રમે...View Solution
- 7ગુચળાનું આત્મપ્રેરકત્વ $5 \,henry$ છે અને તેમાં પ્રવાહ $1 \,amp$ થી $2 \,amp$ થતાં $5\,second$ જેટલો સમય લાગે છે. તો ગુચળામાં પ્રેરિત થતો $e.m.f.$ કેટલા $volt$ હશે?View Solution
- 8$0.01 m^2$ ક્ષેત્રફળ ધરાવતી લૂપ $2\, T$ ચુંબકીયક્ષેત્રને લંબ છે,$10^{-3} seconds$ સમયમાં ચુંબકીયક્ષેત્ર $1\,T$ થાય છે,જો લૂપનો અવરોધ $0.0.1\,Ω$ હોય,તો લૂપમાં કેટલા .......$J$ ઉષ્મા ઉત્પન્ન થાય?View Solution
- 9જ્યારે કોઈલમાં પ્રવાહ એ $0.15$ માં $5\;A$ થી $2\; A$ સુધી બદલાય, તો સરેરાશ વોલ્ટેજ $50\,V$ નો પેદા થાય છે. કોઈલનું આત્મપ્રેરણ $.............\,H$View Solution
- 10View Solutionટ્રાન્સફોર્મરનો કોર શેનો બનેલો હોય છે.
