$0.5 m$ લંબાઇ અને $2 \times 10^{-4} kg$ દળ ધરાવતી દોરીમાં તણાવ $20N$ હોય,તો દ્વિતીય આવૃત્તિ કેટલી .... $Hz$ થાય?
Medium
Download our app for free and get started
d
(d) Mass per unit length \(m = \frac{{2 \times {{10}^{ - 4}}}}{{0.5}}kg/m\)
(d) Mass per unit length \(m = \frac{{2 \times {{10}^{ - 4}}}}{{0.5}}kg/m\)
\( = 4 \times {10^{ - 4}}kg/m\)
Frequency of \(2^{nd}\) harmonic \({n_2} = 2{n_1}\)
\( = 2 \times \frac{1}{{2l}}\sqrt {\frac{T}{m}} \)\( = \frac{1}{{0.5}}\sqrt {\frac{{20}}{{4 \times {{10}^{ - 4}}}}} = 447.2Hz\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક નાનું સ્પીકર $2\, W$ નું અવાજ આઉટપુટ આપે છે.સ્પીકરથી કેટલા ... $cm$ અંતરે અવાજની તીવ્રતા $120\, dB$ નોંધાશે? [સંદર્ભ અવાજની આવૃતિ $10^{-12}\,W/m^2$ છે]View Solution
- 2दो तरंगों के समीकरण निम्न हैंView Solution
${x_1} = a\sin (\omega \,t + {\phi _1})$, ${x_2} = a\sin \,(\omega \,t + {\phi _2})$
यदि परिणामी तरंग में आवृत्ति एवं आयाम अध्यारोपित होने वाली तरंगों के समान हैं तब इनके मध्य कलान्तर होगा
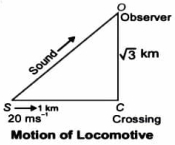
- 3ક્રોસિંગ નજીક પહોંચતી ટ્રેનની ઝડ૫ $20 \,ms ^{-1}$ છે. તે જ્યારે ક્રોસિંગથી $1 \,km$ દુર હોય ત્યારે $640 \,Hz$ આવૃતિની સીટી વગાડે છે. હવા શાંત છે અને હવામાં અવાજની ઝડપ $330\,ms ^{-1}$ છે. ક્રોસિંગથી લંબ રીતે $\sqrt{3} \,km$ દૂર ઉભેલા શ્રોતા વડે ........ $Hz$ આવૃતિ સંભળાશે.View Solution
- 4બે કણોના સ્થાનાંતરView Solution
$ {y_1} = 0.06\sin 2\pi (1.04t + {\phi _1}) $ અને
$ {y_2} = 0.03\sin 2\pi (1.04t + {\phi _2}) $
હોય,તો તેને ઉત્પન્ન કરતાં તરંગની તીવ્રતાનો ગુણોત્તર કેટલો થાય?
- 5ઉદ્ગમથી $1m$ અંતરે ધ્વનિની તીવ્રતા $40dB$ છે,માણસની થ્રેશોલ્ડ તીવ્રતા $20dB$ હોય,તો કેટલા ... $m$ મહત્તમ અંતર સુધી તે અવાજ સાંભળી શકે?View Solution
- 6નકકર ધાતુના ભોયતયિળા પર $ 1\; m $ લંબાઇનો એક ધાતુનો સળિયો એકદમ શિરોલંબ છોડવામાં આવે છે.ઓસિલોસ્કોપ વડે એ શોધવામાં આવ્યું કે અથડામણ $1.2 \;kHz$ આવૃતિના સંગત તરંગ ઉત્પન્ન કરે છે. આ ધાતુના સળિયામાં ધ્વનિની ઝડપ ($m/s$ માં) કેટલી હશે?View Solution
- 7એક સીધી રેખામાં ગતિ કરતાં લંબગત તરંગમાં બે શૃંગ વચ્ચેનું અંતર $5 \,m $ જ્યારે એક શૃંગ અને ગર્ત વચ્ચેનું અંતર $1.5 \,m$ છે. તો તરંગની શક્ય તરંગલંબાઈ ($m$ માં) કેટલી હશે?View Solution
- 8સમાન દ્રવ્ય ધરાવતા બે તારની લંબાઇ $L$ એ $2L $ છે,તેમની ત્રિજયા $ 2r$ અને $r$ છે,બંનેમાં સમાન તણાવ હોય,તો મૂળભૂત આવૃત્તિનો ગુણોત્તર કેટલો થાય?View Solution
- 9એક સ્વર કાંટાને $1 \mathrm{~m}$ લંબાઈના તાર સાથે ખેંચીને બાંધેલો છે અને તે $6 \mathrm{~N}$ તણાવ બળની અસર હેઠળ અજ્ઞાત આવૃત્તિ સાથે અનુનાદ ઉત્પન્ન કરે છે. જો આ જ તારમાં તણાવ બળ બદલીને $54 \mathrm{~N}$ કરવામાં આવે તો તે પ્રતિ સેકન્ડ $12$સ્પંદ ઉત્પન્ન કરે છે. તો સ્વરકાંટાની આવૃત્તિ __________$\mathrm{Hz}$ che.View Solution
- 10$100 \,Hz$ આવૃત્તિ વાળું તરંગ દોરી પર દઢ છેડા તરફ જાય છે. જ્યારે આ તરંગ પરાવર્તન પામીને પાછું આવે ત્યારે દઢ છેડાથી $10\,cm$ અંતરે નિસ્પંદ બિંદુ બને છે. આપત (અને પરાવર્તિત) તરંગની ઝડપ ($m/s$ માં) કેટલી થાય?View Solution