$[A]$ $A$ માંથી દાખલ થતો વિદ્યુત પ્રવાહ $I$ લો અને ચોસલામાં તે એક અર્ધ ગોળાકાર સપાટી ઉપર પ્રસરે છે. તેમ માનવામાં આવે.
$[B]$ઓહમને નિયમ $E = \rho j $ ને ઉપયાગ કરીને $A$ થી $r$ અંતરે વિદ્યુત ક્ષેત્ર $E (r)$ ગણવામાં આવે જ્યાં $j,r$ આગળ દર એકમ ક્ષેત્રફળે વિદ્યુત પ્રવાહ છે.
$[C]$ $E (r)$ નાં $r$ પરનાં આધારપણા પરથી $r$ આગળ સ્થિતિમાન $V (r)$ મેળવવામાં આવે.
$[D]$$D$ માંથી મહાર નીકળતા ($D$ ને છોડતા) વિદ્યુત પ્રવાહ $ I$ માટે $(i)$ અથવા
$B$ અને $C$ વચ્ચે માપવામાં આવતો $\Delta V$ ............ થાય.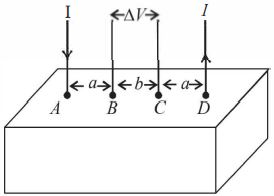
Let \( j\) be the current density.
Then \(j \times 2 \pi r^{2}=I \Rightarrow j=\frac{I}{2 \pi r^{2}} \therefore E=\rho j=\frac{\rho I}{2 \pi r^{2}}\)
Now, \(\Delta V_{BC}^\prime = - \int\limits_{a + b}^a {\vec E} .\overline {dr} = - \int\limits_{a + b}^a {\frac{{\rho I}}{{2\pi {r^2}}}dr} \)
\(=-\frac{\rho I}{2 \pi}\left[-\frac{1}{r}\right]_{a+b}^{a}=\frac{\rho I}{2 \pi a}-\frac{\rho I}{2 \pi(a+b)}\)
On applying superposition as mentioned we get
\(\Delta V_{B C}=2 \times \Delta V_{B C}^{\prime}=\frac{\rho I}{\pi a}-\frac{\rho I}{\pi(a+b)}\)
Download our appand get started for free
Similar Questions
- 1એક ઈલેક્ટ્રિક બલ્નનું રેટિંગ $220 \;V$ અને $100 \;W$ છે જ્યારે તેને $110\;V$ નાં સપ્લાય સાથે જોડવામાં આવે તો કેટલો પાવર વપરાય?View Solution
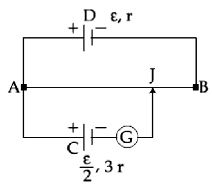
- 2$L$ લંબાઇનો અને $12\, r$ નો અવરોધ ધરાવતા એક પોટેન્શીયોમીટર તાર $AB$ અને $\varepsilon$ જેટલું $emf$ અને $r$ જેટલો આંતરિક અવરોધ ધરાવતા કોષ $D$ સાથે જોડવામાં આવે છે. $\varepsilon/2$ જેટલું $emf$ અને $3r$ જેટલો આતંરિક અવરોધ ધરાવતા કોષ $C$ ને આકૃતિમાં દર્શાવ્યા મુજબ જોડવામાં આવે છે. ગેલ્વેનોમીટરમાં દર્શાવતું શૂન્ય આવર્તન માટેની લંબાઈ $AJ$ _______ હશે.View Solution
- 3$R_1 $ અને $ R_2 $ અવરોધના શ્રેણી અને સમાંતરના સમતુલ્યનો ગુણોત્તર $n$ હોય,તો...View Solution
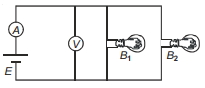
- 4બે એકસમાન બલ્બોને $emf$ $E$ ધરાવતાં આદર્શ ઉદગમની વચ્ચે સમાંતર જોડેલ છે.એમીટર $A$ અને વોલ્ટમીટર $V$એ આદર્શ છે.જો બલ્બ $B_2$એ ફ્યુઝ થઇ જાય તો,View Solution
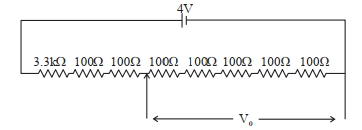
- 5આકૃત્તિમાં એક પોટેન્શિયલ વિભાજક (ડીવાઈડર) પરિપથ દર્શાવેલ છે. આઉટપુટ વોલ્ટેજ$V_0$_______થશે.View Solution
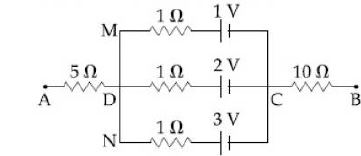
- 6આપેલ પરિપથમાં $A$ અને $B$ વચ્ચેનો સ્થિતિમાનનો તફાવત કેટલા ................. $V$ થાય?View Solution
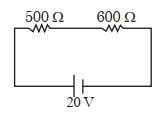
- 7આકૃતિમાં દર્શાવ્યા મુજબ બે અવરોધોને બેટરી સાથે શ્રેણીમાં જોડવામાં આવ્યા છે. જો $2000 \,\Omega$ અવરોધ ધરાવતું વોલ્ટમીટર $500 \,\Omega$ અવરોધને સમાંતર સ્થિતિમાનનો તફાવત માપવા માટે ઉપયોગમાં લેવામાં આવે તો વોલ્ટમીટરમાં ........ $V$નું અવલોકન (રિડિંગ) મળશે.View Solution
- 8બે સમાન બેટરી જેનો $e.m.f.$ $2\, volt$ અને આંતરિક અવરોધ $1.0\, ohm$ છે તેનો ઉપયોગ $R = 0.5\,ohm$ જેટલા બાહ્ય અવરોધમાંથી પ્રવાહ પસાર કરી ઉષ્મા ઉત્પન્ન કરવા થાય છે. આ બેટરી દ્વારા $R$ અવરોધમાંથી મહત્તમ કેટલો જૂલ પાવર ($watt$ માં) ઉત્પન્ન થશે?View Solution
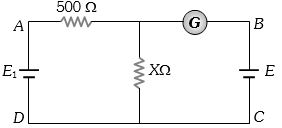
- 9આપેલ પરિપથમાં બેટરી $E_1$ નો $e.m.f.$ $=12\; V$ અને શૂન્ય આંતરિક અવરોધ જ્યારે બેટરી $E$ નો $e.m.f.$ $=2\; V$ છે. જો ગેલ્વેનોમીટરનું અવલોકન શૂન્ય હોય,તો અવરોધ $X $ નું મૂલ્ય કેટલું હશે?View Solution
- 10એક વ્હીસ્ટોન બ્રિજમાં (આકૃતિ જુઓ) ભુજા $P$ અને $Q$ નો ગુણોત્તર લગભગ સરખો છે. જ્યારે $R=400\,\Omega$, બ્રિજ સંતુલન થાય છે. $P$ અને $Q$ ની અદલાબદલી કરતા સંતુલન માટે $R$ નું મૂલ્ય $405\,\Omega$ છે. $X$ નું મૂલ્ય .................. $ohm$ ની નજીકનું હશેView Solution