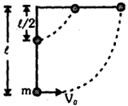
રેખીય વેગમાનના સંરક્ષણ પરથી ,
\(\left( {\text{1}} \right)\,\,u\,\, = \,\, - \left( 1 \right)2\,\, + \;\,\left( 5 \right)\,\,v\,\, \Rightarrow \,\,5v\,\, - \,\,2\,\, = \,\,u\,\,.....\left( i \right)\)
\('e\) ની વ્યાખ્યા પરથી \(1\,\, = \,\,\frac{{v\,\, + \;\,2}}{u}\,\, \Rightarrow \,\,v\,\, + \;\,2\,\, = \,\,u\,\,\,.....\left( {ii} \right) \)
ઉપરનું સમીકરણ ઉકેલતા \(v\,\, = \,\,1\,m{s^{ - 1}}\) અને \(u\,\, = \,\,3\,\,m{s^{ - 1}}\)
\((A) \) માટે તંત્ર નું કુલ વેગમાંન \( = \,\,1\,\, \times \,\,u\,\, = \,\,3\,\,kg\,\,m{s^{ - 1}}\)
\((B) \) માટે અથડામણ બાદ \(5\,\,kg\) દળ નું વેગમન \( = \,\,5\left( 1 \right)\,\, = \,\,5\,\,kg\,\,m{s^{ - 1}}\)
\((C) \) માટે \({K_{cm}}\,\, = \,\frac{1}{2}\,\,\left( {1\,\, + \;\,5} \right)\,\,\left( {\frac{{1\,\, \times \,\,3\,\, + \;\,0}}{{1\,\, + \;\,5}}} \right)\,\, = \,\,0.75\,\,J\)
\((D) \) માટે તંત્ર ની કુલ ગતિ ઉર્જા \( = \,\,\frac{1}{2}\,\,\left( 1 \right)\,{\left( 3 \right)^2}\,\, = \,\,4.5\,\,J\)
Download our appand get started for free
Similar Questions
- 1$8\,kg$ અને $2\,kg$ દળ ધરાવતી બે વસ્તુઓ સમાન ગતિઊર્જા સાથે ગતિ કરે છે. તેઓના વેગમાનોનો ગુણોત્તર $.......$ થશે.View Solution
- 2$m_1$ દળનો એક કણ $m_2$ દળના સ્થિર સ્થિતિએ રહેલા બીજાકણ સાથે સંપૂર્ણ અસ્થિતિ સ્થાપક હેડ ઓન સંઘાત અનુભવે છે. ($m_2$ > $m_1$). આ સંઘાતમાં ઘર્ષણની ગતિઊર્જા કેટલા મૂલ્યની ઉષ્માઊર્જામાં રૂપાંતરણ પામશે?View Solution
- 3જયારે રબરબેન્ડને $x$ અંતરે ખેંચવામાં આવે છે,ત્યારે ઉત્પન્ન થતું પુન:સ્થાપક બળ $F=ax+bx^2$ છે,જયાં $a$ અને $b$ અચળાંક છે.જો રબરબેન્ડને તેની મૂળ સ્થિતિમાંથી $L$ અંતર ખેંચવામાં આવે તો થતું કાર્ય:View Solution
- 4એક બોલને $h_0$ ઉંચાઈએથી ફેંકો. તે પૃથ્વી સાથે $n$ સંઘાત કરે છે. $n$ સંઘાત પછી જો બોલના ઉછળાટનો વેગ $u_n$ હોય અને બોલ $h_n $ ઉંચાઈએ પહોંચતો હોય તો રેસ્ટીટ્યૂશન ગુણાંક ને કયા સૂત્રની મદદથી આપી શકાય?View Solution
- 5પરમાણુના બે અણુઓ વચ્ચેની સ્થિતિઊર્જા $U(x) = \frac{a}{{{x^{12}}}} - \frac{b}{{{x^6}}}$ દ્વારા આપવામાં આવે છે; જ્યાં $a$ અને $b$ એ ધન અચળાંકો છે અને $x$ એ અણુઓ વચ્ચેનું અંતર છે. અણુ સ્થાયી સંતુલનમાં હશે જ્યારે .......View Solution
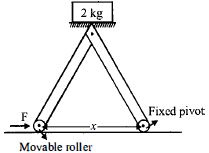
- 6બે સમાન $1\, m$ લંબાઈ ના સળિયા ધરાવતું એક મશીન આકૃતિ માં બતાવ્યા મુજબ ટોચ પર ધરી દ્વારા જોડેલ છે. તેના એક સળિયાનો છેડો જમીન સાથે સ્થિત ધરી દ્વારા જોડેલ છે અને બીજા સળિયાનો છેડો એક રોલર સાથે જોડેલ છે જે જમીન પર એક અમુક અંતર સુધી ફરી શકે . જ્યારે રોલર આગળ પાછળ જાય છે ત્યારે $2\, kg$ નું વજનિયું ઉપર નીચે જાય છે. જો રોલર જમણી તરફ અચળ ઝડપે ગતિ કરે તો વજનિયું ઉપર તરફ .... થી ગતિ કરશે.View Solution
- 7$W$ વજન ધરાવતા ટુકડા દ્વારા $ v$ વેગ સાથે ઘર્ષણરહિત સમક્ષિતિજ સપાટી પર તણાવ લગાડવામાં આવે છે ત્યારે $k$ બળ અચળાંકવાળી સ્પ્રિંગમાં મહત્તમ તણાવ ઉત્પન્ન થાય છે જે ......... અંતરે થશે.View Solution
- 8$\mathrm{m}$ દળ ધરાવતા બે કણનો શરૂઆતનો વેગ $u\hat{i}$ અને $u\left(\frac{\hat{\mathrm{i}}+ \hat{\mathrm{j}}}{2}\right)$ છે. તે બંને અસ્થિસ્થાપક રીતે અથડાય છે, તો આ પ્રક્રિયા દરમિયાન તે કેટલી ઉર્જા ગુમાવશે?View Solution
- 9$400\; ms^{-1}$ ના સમક્ષિતિજ વેગથી ગતિ કરતી $10\;g $ દળની એક ગોળી, $2\; kg $ દળના લાકડાના બ્લોક સાથે અથડાય છે, જે $5\; m$ લાંબી ખેંચાઇ ન શકે તેવી દોરીથી લટકાવેલ છે. જેના લીધે બ્લોકનું ગુરુત્વકેન્દ્ર $10\;cm$ શિરોલંબ અંતર વધે છે. બ્લોકની સમક્ષિતિજ દિશામાં બહાર નીકળે ત્યારે ગોળીની ઝડપ (${ms} ^{-1}$ માં) કેટલી હશે?View Solution
- 10$L$ લંબાઈના એક હલકા સળિયાને ઉપરના છેડાની શરૂઆતમાં મુકેલો છે. બે દળો (દરેકનું $m $ દળ) સળિયા સાથે જોડાયેલા છે. જેમાં એક સળિયાના મધ્યબિંદુએ અને બીજો દળ મુક્ત છેડે છે. નીચેના દળના છેડા આગળ કેટલો સમક્ષિતિજ વેગ લાગુ પાડવો જોઈએ કે જેથી સળિયો સમક્ષિતિજ રીતે રહે.View Solution