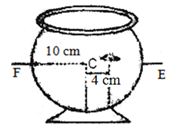
$10\, cm $ ત્રિજ્યાના ગોળાકાર પાત્રને $(4/3)$ વક્રીભવનાંક વાળા પાણીથી ભરેલું છે. આકૃતિમાં બતાવ્યા પ્રમાણે કેન્દ્રથી $4 \,cm$ ના અંતરે એક માછલી છે. જો છેડા $ F$ થી જોવામાં આવે તો માછલી ......$cm$ દેખાતી હશે? (માછલી જોડાઈ અવગણતાં)

Diffcult
d
\(\frac{{{\mu _2}}}{v}\,\, - \,\,\frac{{{\mu _1}}}{u}\,\, = \,\,\,\frac{{({\mu _2} - {\mu _1})}}{R}\,\)
\(\frac{{{\mu _2}}}{v}\,\, - \,\,\frac{{{\mu _1}}}{u}\,\, = \,\,\,\frac{{({\mu _2} - {\mu _1})}}{R}\,\)
છેડા \(f\) થી જોતાં \(\,\,{\mu _1} = \,\,\frac{4}{3}\,,\,\,{\mu _2} = \,\,1\,,\,\,R\,\, = \,\, - 10\,\,cm\) અને \(u\,\, = \,\, - (10 + 4)\,\, = \,\, - 14\,\,cm\)
\(\frac{1}{v}\,\, - \,\,\,\frac{{\frac{4}{3}}}{{ - 14}}\,\,\, = \,\,\frac{{1 - \frac{4}{3}}}{{ - 10}}\,,\,\,\,v\,\, = \,\,\frac{{ - 210}}{{13}}\,\, = \,\,\, - \,\,16.154\,\,\,cm\)
તેથી, માછલી છેડા \(F\) થી \(E\) તરફ \(6.154 \,cm \) અંતરે દેખાતી હશે. (વાસ્તવિક અંતર કરતાં \(14 \,cm\) વધારે)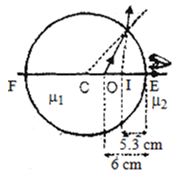
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionમૃગજળ ઘટના કોના કારણે થાય છે.
- 2પાણીમાંથી લીલો પ્રકાશ હવા-પાણી આંતરપૃષ્ઠ પર ક્રાંતિકોણ $\theta $ એ આપાત થાય છે.સાચું વિધાન પસંદ કરો.View Solution
- 3બહિર્ગોળ લેન્સ વડે રચાતા વાસ્તવિક પ્રતિબિંબ અને વાસ્તવિક વસ્તુ વચ્ચેનું અંતર $56\, cm$ છે. તો લેન્સની કેન્દ્રલંબાઈ કેટલી છે.View Solution
- 4View Solutionલઘુધ્ષ્ટિ નિવારવા માટે કયા લેન્સ પહેરવા પડે?
- 5એક નાના ટેલિસ્કોપમાં $140$ $cm$ની કેન્દ્રલંબાઈ ધરાવતો ઓબ્જેક્ટિવ અને $5.0$ $cm$નl કેન્દ્રલંબાઈ ધરાવતો નેત્રકાચ (આઈ પીસ) છે. દૂરની વસ્તુને જોતાં ટેલિસ્કોપની મોટવણી. . . . . . થશે.View Solution
- 6બંને સપાટીની વક્રતાત્રિજ્યા $R$ ધરાવતા બહિગોળ લેન્સનો પાવર $p$ છે તો સમાન દ્રવ્યમાંથી બનાવેલ સમતલ બહિગોળ લેન્સ નો પાવર $1.5P$ હોય તો તેની વક્રતાત્રિજ્યા ........$R$View Solution
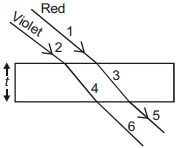
- 7View Solutionલાલ અને જાંબલી રંગનાબે સમાંતર કિરણો કાચના લંબઘનમાંથી પસાર થાય છે, નીચેનામાંથી ક્યું સાચું છે ?
- 8View Solutionટ્રાવેલિંગ માઈક્રોસ્કોપનો ઉપયોગ કરીને કારનો વક્રીભવનાંક નક્કી કરવાના પ્રયોગમાં અંતર કેવી રીતે માપવામાં આવે છે.
- 9$20\,cm$ કેન્દ્ર લંબાઈના બે બહિર્ગોળ લેન્સને સમઅક્ષીય રીતે એકબીજાથી $60\; cm$ દૂર મુકેલા છે. દૂરના અંતરે રહેલી વસ્તુનું સંયોજન વડે રચાતું પ્રતિબિંબ પ્રથમ લેન્સથી .......... $cm$ અંતરે હશે.View Solution
- 10View Solutionપોલા કાચના ગોળામાંથી ગોળીય અરીસો બનાવવામાં આવે છે. અરીસાની સામે વસ્તુ મુક્તા પ્ર્તિબિંબ અને મોટવણી