$10\; g$ દળનો એક કણ $ 6.4\; cm$ ત્રિજયાના વર્તુળાકાર માર્ગ પર અચળ સ્પર્શીય પ્રવેગથી ગતિ કરે છે. જો ગતિની શરૂઆત પછી બીજું પરિભ્રમણ પૂરું કરે ત્યારે કણની ગતિઊર્જા $8 \times 10^{-4} J $ થઇ જાય, તો આ પ્રવેગનું મૂલ્ય ($m/s^{2}$ માં) કેટલું હશે?
NEET 2016, Medium
d
\(\begin{gathered}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,Here,\,m = 10\,g\, = {10^{ - 2}}\,kg, \hfill \\
R = 6.4\,cm = 6.4 \times {10^{ - 2}}m,\,{K_f} = 8 \times {10^{ - 4}}\,J, \hfill \\
{K_i} = 0,\,{a_{t = }}? \hfill \\
{\text{Using}}\,work\,energy\,theorem, \hfill \\
Work\,done\,by\,all\,the\,forces = Change\,in\,KE \hfill \\
{W_{\tan gential\,force\,}} + {W_{centripetal\,force}} = {K_f} - {K_i} \hfill \\
\Rightarrow {a_t} = \frac{{{K_f}}}{{4\pi Rm}} = \frac{{8 \times {{10}^{ - 4}}}}{{4 \times \frac{{22}}{7} \times 6.4 \times {{10}^{ - 2}} \times {{10}^{ - 2}}}} \hfill \\
\,\,\,\,\,\,\,\,\,\,\,\, = 0.099 \approx 0.1\,m\,{s^{ - 2}} \hfill \\
\end{gathered} \)
\(\begin{gathered}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,Here,\,m = 10\,g\, = {10^{ - 2}}\,kg, \hfill \\
R = 6.4\,cm = 6.4 \times {10^{ - 2}}m,\,{K_f} = 8 \times {10^{ - 4}}\,J, \hfill \\
{K_i} = 0,\,{a_{t = }}? \hfill \\
{\text{Using}}\,work\,energy\,theorem, \hfill \\
Work\,done\,by\,all\,the\,forces = Change\,in\,KE \hfill \\
{W_{\tan gential\,force\,}} + {W_{centripetal\,force}} = {K_f} - {K_i} \hfill \\
\Rightarrow {a_t} = \frac{{{K_f}}}{{4\pi Rm}} = \frac{{8 \times {{10}^{ - 4}}}}{{4 \times \frac{{22}}{7} \times 6.4 \times {{10}^{ - 2}} \times {{10}^{ - 2}}}} \hfill \\
\,\,\,\,\,\,\,\,\,\,\,\, = 0.099 \approx 0.1\,m\,{s^{ - 2}} \hfill \\
\end{gathered} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વેઇટ લિફટર $300\; kg$ જેટલુ વજન $3 $ સેકન્ડમાં જમીનથી $2\;m$ ઉંચાઇએ ઉચકે છે તો તેના દ્વારા ઉત્પન્ન થતો સરેરાશ પાવર.....$watt$View Solution
- 2$1\, m$ લંબાઇ અને ${60^o}$ ખૂણાવાળા ઢાળ પર $1\, kg$ નો બ્લોક મૂકતાં ઘર્ષણ વિરુધ્ધ ...... $J$ કાર્ય થશે. (ગતિક ઘર્ષણાંક $0.5$ છે)View Solution
- 3એક $m$ દળવાળા સ્થિર પદાર્થને પ્રવેગ આપતાં તે $T$ સમયમાં $v$ જેટલો વેગ પ્રાપ્ત કરે છે. સમયના પદમાં પદાર્થને મળતો તત્કાલીન પાવર ........છે.View Solution
- 4$m $ દળ અને $ v$ વેગની એક ગોળી $M$ દળના લોલક આગળથી પસાર થાય છે અને $v/2$ વેગ સાથે અથડાય છે. $v$ ની કઈ ન્યૂનત્તમ કિંમત માટે લોલક સંપૂર્ણ ચક્ર પૂર્ણ કરશે ?View Solution
- 5એક એકરેખીક અથડામણમાં $v_0$ જેટલી પ્રારંભિક ઝડપ ધરાવતો કણ બીજા તેટલું જ દળ ધરાવતા સ્થિર કણ સાથે અથડાય છે.જો અંતિમ કુલ ગતિઊર્જા,પ્રારંભિક ગતિઊર્જા કરતાં $50\%$ અધિક છે.તો અથડામણ બાદ, બે કણો વચ્ચે સાપેક્ષ વેગનું પરિમાણ હશે.View Solution
- 6$m $ દળનું એક વાહન સ્થિર સ્થિતિએથી પ્રવેગીત થાય છે. જો એન્જિન $p$ જેટલો અચળ પાવર અપાતુ હોય તો $ t $ સમયે વેગ કયા સૂત્રથી આપી શકાય?View Solution
- 7$0.2$ ઘર્ષણાંક ધરાવતી સમક્ષિતિજ સપાટી પર $5 kg $ નો પદાર્થ પડેલો છે. તેને $25 N $ ના સમક્ષિતિજ બળ વડે $10 m$ ખેંચવામાં આવે છે. પદાર્થેં મેળવેલી ગતિઊર્જા .....$J$ છે. ($g = 10 ms^{-2} $ લો.)View Solution
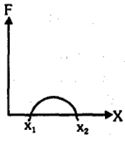
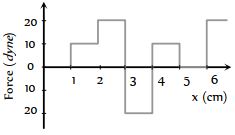
- 8આકૃતિમાં બળ અને સ્થાન વચ્ચેનો સંબંધ બતાવ્યો છે. $x = 1 \;cm$ થી $x = 5 \;cm $ સુધી પદાર્થના સ્થાનાંતર માટે બળ દ્વારા થતું કાર્ય કેટલા ......અર્ગ હશે ?View Solution
- 9આપેલ આકૃતિ અનુસાર, $250\,g$ ના બે ચોસલાઓને $2\,Nm^{-1}$ સ્પ્રિંગ અચળાંક ધરાવતી સ્પ્રિંગ સાથે જોડવામાં આવેલ છે. જો બંને વિરુદ્ધ દિશામાં $v$ જેટલો વેગ આપવામાં આવે તો સ્પ્રિંગમાં મહત્તમ વિસ્તરણ $...........$ જેટલું થશે.View Solution

- 10$x$ અક્ષ પર ગતિ કરતા એક પદાર્થ પર બળ લાગે છે જેનું સ્થાન આકૃતિમાં દર્શાવ્યા પ્રમાણે બદલાય છે. પદાર્થ કયા બિંદુએ સ્થાયી સંતુલન સ્થિતિએ હશે.View Solution