$10\, N$ અને $6\, N$ બે બળોનો સદિશ સરવાળો ......... $N$ થઈ શકે નહીં
Easy
Download our app for free and get started
d
Magnitude of \(\overrightarrow{ A }+\overrightarrow{ B }\) has to lie between \(A - B\) and \(A + B\), i.e \(10-6\) and \(10+6\), or \(4\) and \(16\).\(2\) is out of this range, hence it's the correct answer.
Magnitude of \(\overrightarrow{ A }+\overrightarrow{ B }\) has to lie between \(A - B\) and \(A + B\), i.e \(10-6\) and \(10+6\), or \(4\) and \(16\).\(2\) is out of this range, hence it's the correct answer.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો $\mathop {\,{\rm{A}}}\limits^ \to \,\, + \;\,\mathop {\rm{B}}\limits^ \to \,\, = \,\mathop {\rm{C}}\limits^ \to $ અને $ {\rm{A}}\,\, + \;\,{\rm{B}}\,\, = \,\,{\rm{C}}\,$ હોય $\vec A $ અને $\vec B $ વચ્ચેનો ખૂણો કેટલો થાય .View Solution
- 2બે સદિશો $ \hat i - 2\hat j + 2\hat k $ અને $ 2\hat i + \hat j - \hat k, $ માં કયો સદિશ ઉમેરવાથી $X-$ દિશામાંનો એકમ સદિશ મળે.View Solution
- 3કોલમ $-I$ ને કોલમ $-II$ સાથે જોડો.View Solution
કોલમ $-I$ કોલમ $-II$ $(1)$ બે સદિશોનું સંયોજન મહત્તમ $(a)$ $180^o$ $(2)$ બે સદિશોનું સંયોજન ન્યૂનતમ $(b)$ $90^o$ $(c)$ $0^o$ - 4લિસ્ટ $- I$ ને લિસ્ટ $- II$ સાથે જોડોView Solution
નીચેના વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો
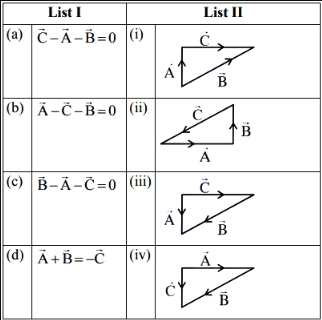
- 5બે $F$ મૂલ્યના બળોના પરિણામી બળનું મૂલ્ય $F$ હોય તો તે બે બળો વચ્ચેનો ખૂણો ....... $^o$ હશે.View Solution
- 6$A = 3\hat i + 4\hat j$ અને $B = 7\hat i + 24\hat j$ છે, $B$ ના મૂલ્ય જેટલો અને $A$ ને સમાંતર સદિશ મેળવો.View Solution
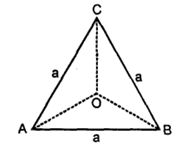
- 7$ABC$ એ સમબાજુ ત્રિકોણ છે. દરેક બાજુની લંબાઈ $'a'$ અને તેનું પરિકેન્દ્ર $O$ છે. તો $\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=.......$View Solution
- 8કોઈ સદિશ $\vec A $ માથી એક નવો સદિશ $\vec B$ મેળવવા માટે તેને $\Delta \theta$ રેડિયન $( \Delta \theta << 1)$ જેટલું કોણાવર્તન કરાવવામાં આવે છે. તો આ કિસ્સામાં $\left| {\vec B - \vec A} \right|$ શું થશે?View Solution
- 9સદિશ $ (\hat i + \hat j) $ અને $ (\hat j + \hat k) $ વચ્ચેનો ખૂણો ....... $^o$ થશે.View Solution
- 10$ \overrightarrow a \,.\,\overrightarrow b = 0 $ અને $ \overrightarrow a \,.\,\overrightarrow c = 0. $ હોય,તો $ \overrightarrow a $ કોને સમાંતર થશે?View Solution