$10kg $ ના સ્થિર પદાર્થ પર $ 4 N $ અને $3N $ ના પરસ્પર લંબ બળો લાગતાં હોય,તો $10 sec $ પછી ગતિઊર્જા.....$J$
Medium
Download our app for free and get started
d
\(F = \sqrt {{4^2} + {3^2}} = 5N\)
\(F = \sqrt {{4^2} + {3^2}} = 5N\)
\(K= w = F s = F \times \frac{1}{2}a\,{t^2} = F \times \frac{1}{2}\left( {\frac{F}{m}} \right)\,{t^2}\)
\( = 5 \times \frac{1}{2}\left( {\frac{5}{{10}}} \right)\,{(10)^2} = 125\)\(J.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
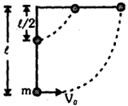
- 1$L$ લંબાઈના એક હલકા સળિયાને ઉપરના છેડાની શરૂઆતમાં મુકેલો છે. બે દળો (દરેકનું $m $ દળ) સળિયા સાથે જોડાયેલા છે. જેમાં એક સળિયાના મધ્યબિંદુએ અને બીજો દળ મુક્ત છેડે છે. નીચેના દળના છેડા આગળ કેટલો સમક્ષિતિજ વેગ લાગુ પાડવો જોઈએ કે જેથી સળિયો સમક્ષિતિજ રીતે રહે.View Solution
- 2એક કણ એક જ દિશામાં સમક્ષિતિજ સમતલમાં અચળ પાવર હેઠળ ગતિ કરે છે.આ ગતિ કરતાં કણ માટે સ્થાનાંતર $(s)$ વિરુદ્ધ સમય $(t)$ નો આલેખ નિચે પૈકી કેવો મળે?View Solution
- 3પ્રક્ષિપ્ત ગતિમાં ${m_1}$ અને ${m_2}$ દળ ધરાવતા બે કણો માટે $t = 0$ સમયે વેગ અનુક્રમે ${\vec v_1}$ અને ${\vec v_2}$ છે. તેઓ ${t_0}$ સમયે સંઘાત પામે છે. તેથી $2{t_0}$ સમયે ${\vec v_1}'$ અને ${\vec v_2}'$ વેગથી હવામાં ગતિ કરે છે. તો $|({m_1}\overrightarrow {{v_1}} '\, + {m_2}\overrightarrow {{v_2}} ') - ({m_1}\overrightarrow {{v_1}} \, + {m_2}\overrightarrow {{v_2}} )$| ની કિંમત શું થશે?View Solution
- 4$1\, m$ લંબાઈ સાથે બાંધેલ એક નાનો ગોળો એક ઉર્ધ્વ વર્તુળ દર્શાવે છે કે જેથી દોરીઓમાં મહત્તમ અને ન્યૂનતમ તણાવનો ગુણોત્તર $5:1$ છે. ગોળાનો સૌથી ઉચ્ચતમ સ્થાન પાસે વેગ ............ $m /s$ છે. $(g =10\, m/s^2$ લો.)View Solution
- 5$v $ વેગથી $m$ દળનો કણ સ્થિર રહેલા $2m$ દળના કણ સાથે અથડાઇને ચોંટી જાય છે.તો સંયુકત વેગ કેટલો થાય?View Solution
- 6$m = 10\,kg$ દળનો એક બ્લોક સમક્ષિતિજ ટેબલ પર સ્થિર પડેલો છે. બ્લોક અને ટેબલ વચ્ચે નો ઘર્ષણાંક $0.05$ છે.જ્યારે $50\,g$ દળ ધરાવતી એક બુલેટ $v$ વેગથી બ્લોકમાં ઘૂસે છે, તેથી બ્લોક ટેબલ પર $2\,m$ અંતર કાપીને સ્થિર થાય છે.જો મુક્ત પતન કરતા પદાર્થને $\frac {v}{10}$ વેગ જાળવવો હોય તો ઉર્જાના વ્યયને અવગણતા અને $g=10\,ms^{-2}$ લેતા $H$ ની કિંમત ................... $\mathrm{km}$ થશે?View Solution
- 7સાદા લોલકની દોરીની તણાવ ક્ષમતા ગોળાના વજન કરતાં બમણી છે, દોરી સમક્ષિતિજ રહે તે રીતે ગોળાને મૂકવામાં આવે ત્યારે દોરી શિરોલંબ સાથે કેટલાના $\theta $ ખૂણે તૂટશે?View Solution
- 8View Solutionપૃથ્વી પરથી શિરોલંબ રીતે ઉપરની તરફ પ્રક્ષેપિત પદાર્થ પૃથ્વી પર પાછા આવતા પહેલા પૃથ્વીની ત્રિજ્યા જેટલી ઊંચાઈએ પહોંચે છે. ગુરુત્વાકર્ષણ બળ દ્વારા લગાવવામાં આવતો પાવર મહત્તમ .........
- 9પદાર્થને $h_1$ ઉંચાઈથી જમીન પર છોડવામાં આવે છે અને જમીન પર અથડાયા પછી, તે $h _2$ ઉંચાઈ સુધી ઉછળે છે. જો જમીન પર અથડાતા પહેલા અને પછી પદાર્થના વેગનો ગુણોત્તર $4$ હોય, તો પદાર્થની ગતિ ઊર્જામાં પ્રતિશત ત્રુટિ $\frac{x}{4}$ છે. $x$ નું મૂલ્ય ...... છેView Solution
- 10$10 kg$ દળનો એક પદાર્થ $ (\theta = 30° )$ લીસા ઢોળાવ વાળા સમતલ પર અચળ વેગથી $10 m$ અંતર કાપે છે તો પદાર્થ વડે થતું કાર્ય ......... $J$ ગણો. $[g = 10 m/s^2]$View Solution