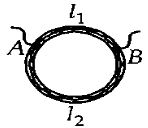
Let \(x\) be resistance per unit length of the wire. Then,
The resistance of the upper portion is
\(R_{1}=x l_{1}\)
The resistance of the lower portion is
\(R_{2}=x l_{2}\)
Equivalent resistance between \(A\) and \(B\) is
\(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{\left( {x{l_1}} \right)(x{l_2})}}{{x{l_1} + x{l_2}}}\)
\(\frac{8}{3}=\frac{x l_{1} l_{2}}{l_{1}+l_{2}}\) or \(\frac{8}{3}=\frac{x l_{1} l_{2}}{l_{2}\left(\frac{l_{1}}{l_{2}}+1\right)}\) or \(\frac{8}{3}=\frac{x_{1}}{\left(\frac{l_{1}}{l_{2}}+1\right)}\) ......\((i)\)
Also \(\quad R_{0}=x l_{1}+x l_{2}\)
\({12=x\left(l_{1}+l_{2}\right)}\)
\({12=x l_{2}\left(\frac{l_{1}}{l_{2}}+1\right)}\) ....\((ii)\)
Divide \((i)\) by \((ii),\) we get
\(\frac{{\frac{8}{3}}}{{12}} = \frac{{\frac{{x{l_1}}}{{\left( {\frac{{{l_1}}}{{{l_2}}} + 1} \right)}}}}{{x{l_2}\left( {\frac{{{l_1}}}{{{l_2}}} + 1} \right)}}{\rm{ or }}\frac{8}{{36}} = \frac{{{l_1}}}{{{l_2}{{\left( {\frac{{{l_1}}}{{{l_2}}} + 1} \right)}^2}}}\)
\(\left(\frac{l_{1}}{l_{2}}+1\right)^{2} \frac{8}{36}=\frac{l_{1}}{l_{2}}\) or \(\left(\frac{l_{1}}{l_{2}}+1\right)^{2} \frac{2}{9}=\frac{l_{1}}{l_{2}}\)
Let \(y=\frac{l_{1}}{l_{2}}\)
\(\therefore\) \(2(y+1)^{2}=9 y\) or \(2 y^{2}+2+4 y=9 y\)
or \( 2 y^{2}-5 y+2=0\)
Solving this quadratic equation, we get
\(y=\frac{1}{2}\) or \(2 \therefore \frac{l_{1}}{l_{2}}=\frac{1}{2}\)
Download our appand get started for free
Similar Questions
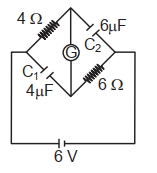
- 1પરિપથમાં આપેલ ગેલ્વેનોમીટર $(G)$ નો અવરોધ $2 \Omega$ હોય તો પરિપથમાં આપેલ $C_1$ અને $C_2$ પરનો વિદ્યુતભારનો ગુણોતર કેટલો થાય.View Solution
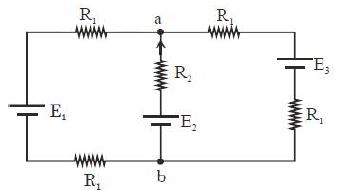
- 2આપેલ પરિપથમાં ${R_1} = 1.0\,\Omega $, ${R_2} = 2.0\,\Omega $, ${E_1} = 2\,V$ અને ${E_2} = {E_3} = 4\,V$ હોય તો બિંદુ $‘a’$ અને $‘b’$ વચ્ચે વિદ્યુતસ્થિતિમાનનો તફાવત કેટલો મળે?View Solution
- 3$0\,^oC$ તાપમાને પ્લેટીનીયમ અવરોધ થર્મોમીટરમાં કોઈલનો અવરોધ $5$ ઓહમ છે $100\,^oC$ અને તાપમાને $5.75$ ઓહમ છે. અજ્ઞાત તાપમાને તેનો અવરોધ $5.15 $ ઓહમ છે. તો અજ્ઞાત તાપમાન ............ $^oC$ હશે.View Solution
- 4પોટેન્શિયોમિટર તારની લંબાઈ $4\,m$ છે અને અવરોધ $10\,\Omega$ છે. તેને $2 \,V \,emf$ ધરાવતા કોષ સાથે જોડવામાં આવે છે. તારની એકમ લંબાઈ દીઠ સ્થિતિમાનનો તફાવત ........... $V/m$ હશે.View Solution
- 5$20\, \Omega $ સરેરાશ અવરોધ ધરાવતી ઈલેક્ટ્રિક કીટલીમાં $20\,^oC$ તાપમાને રહેલ એક $kg$ પાણી ગરમ કરવામાં આવે છે.મેઇનનો $rms$ વૉલ્ટેજ $200\, V$ છે.કીટલીમાં થતો ઉષ્માનો વ્યયને અવગણતા કિટલીમાં રહેલ પાણીને વરાળમાં ફેરવવા ....... $(\min)$ સમય લાગે? [ પાણીની વિશિષ્ટ ઉષ્મા $= 4200\, J/kg\, ^oC$, પાણીની બાષ્પાયન ગુપ્ત ઉષ્મા $= 2260\, k\,J/kg$]View Solution
- 6ચોરસની બાજુઓ $AB, BC, CD $ અને $ DA $ પર અનુક્રમે $10\, \Omega, 5\, \Omega, 7\, \Omega$ અને $ 3 \,\Omega $ અવરોધ જોડવામાં આવે છે,વિકીર્ણ $ AC$ પર $10 \,\Omega$ અવરોઘ જોડવામાં આવે તો $A $ & $ B $ ની વચ્ચે સમતુલ્ય અવરોધ કેટલા ............... $\Omega$ થાય?View Solution
- 7પોટેન્શીયોમીટર $4\,m$ લંબાઈ તથા $10\, \Omega$ અવરોધવાળો તાર ધરાવે છે. પોટેન્શીયોમીટરને $2\,V$ ધરાવતા કોષ સાથે જોડવામાં આવે છે. તો એકમ લંબાઈ દીઠ વિધુતસ્થીતિમાનનો તફાવત........... $V/m$ હશે.View Solution
- 8નીચે આપેલા જાળતંત્ર માટે, સ્થાયી અવસ્થા માટે સંગ્રહાકમાં સંધારક સંગ્રહીત થતી વીજભાર .............. $\mu C$ હશે.View Solution
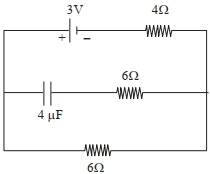
- 9View Solutionધાતુના તારના બે છેડા વચ્ચે અચળ વિદ્યુતસ્થિતિમાનનો તફાવત લગાવવામાં આવે છે. જો તારની લંબાઈ અડધી અને ત્રિજ્યા બમણી કરવામાં આવે તો તેમાંથી ઉત્પન્ન થતી ઉર્જાનો દર....
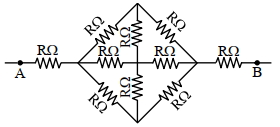
- 10જો દરેક અવરોધ $R$ હોય તો $A$ અને $B$ વચ્ચેનો અસરકારક અવરોધ .......... થશે.View Solution