\(M_1 \) અરીસા માટે \(O\) વસ્તુ તરીકે વર્તે છે. ધારો કે તેનું પ્રતિબિંબ \(I_1\) છે તો \(u = -15 cm, f = -10 cm\)
\( \Rightarrow \,\,\frac{1}{v} + \,\,\frac{1}{{ - 15}}\,\,\, = \,\,\frac{1}{{ - 10}}\,\,\,\, \Rightarrow \,\,\,v\,\, = \,\,\, - 30\,\,cm\)
પ્રતિબિંબ \(I_1\) \(M_2\) અરીસા માટે વસ્તુ તરીકે વર્તશે અને \(M_2\) અરીસાથી તેનું અંદર \(M_2\) છે
\({u_1} = \,\, - (40 - 30)\,\,\,cm\,\,\, = \,\, - 10\,\,\,cm\,\,\,\,\,\)
\( \Rightarrow \,\,\frac{1}{{{v_1}}}\,\, + \,\,\frac{1}{{{u_1}}}\,\,\, = \,\,\,\,\frac{1}{{f}}\,\,\,\,\, \Rightarrow \,\,\frac{1}{{{v_1}}} - \,\,\frac{1}{{10}}\,\, = \,\,\frac{1}{{15}}\,\,\,\,\, \Rightarrow \,\,{v_1} = \,\, + \,\,6\,\,cm\)
તેથી અંતિમ પ્રતિબિંબ બહિર્ગોળ અરીસાની પાછળ \(6\,\, cm\) અંતરે રચાય છે. અને વાસ્તવિક હોય છે.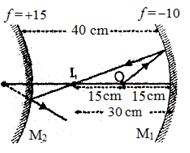
Download our appand get started for free
Similar Questions
- 1View Solutionઆપેલ પ્રિઝમનો પ્રિઝમકોણ કયો છે?
- 2અંતર્ગોળ અરીસાની કેન્દ્રલંબાઈ $30\, cm $છે. જો પ્રતિબિંબ ઊલટું (વાસ્તવિક) હોય તો, અરીસાના સામે રહેલી વસ્તુ નું સ્થાન....$cm$ અંતરે હોઈ શકે જેથી પ્રતિબિંબ વસ્તુના કદ કરતાં ત્રણ ગણું હોય.View Solution
- 3લેન્સથી $2.4\; m$ ના અંતરે રહેલ વસ્તુનું પ્રતિબિંબ લેન્સની પાછળ $12 \;cm$ અંતરે રહેલ પડદા પર મળે છે. $1\; cm$ જાડાઈની અને $1.5$ વક્રિભવનાંક ધરાવતી કાચની એક પ્લેટને લેન્સ અને પડદાની વચ્ચે, તેનું સમતલ પડદાને સમાંતર રહે તેમ મૂકવામાં આવે તો હવે વસ્તુ લેન્સથી કેટલે દૂર ખસેડવી પડે કે જેથી તેનું પ્રતિબિંબ પડદા પર ઝિલાય?View Solution
- 4એક સમતલ અરીસાને $10 \,\,cm$ કેન્દ્રલંબાઈના અંત:ર્ગોળ અરીસાથી $22.5\,\, cm$ ના અંતરે મૂકેલો છે. બે અરીસાઓ વચ્ચે વસ્તુને .....$cm$ મૂકી શકાય કે જેથી બંન્ને અરીસામાં પ્રથમ પ્રતિબિંબ ભેગા મળે ?View Solution
- 5લઘુ દ્રષ્ટિ માટે દૂરનું બિંદુ $40\, cm$ અંતરે છે. ખામી નિવારવા માટે કેટલા પવારનો લેન્સ પહેરવો પડે?View Solution
- 6ખામી અને નિવારવાના ઉપાયો જોડો.View Solution
$(I)$ મોતિયો $(A)$ નળાકાર લેન્સ $(II)$ ગુરુદ્રષ્ટિ $(B)$ બહિર્ગોળ લેન્સ $(III)$ એસ્ટિગ્મેટીઝમ $(C)$ અંતર્ગોળ લેન્સ $(IV)$ લઘુદ્રષ્ટિ $(D)$ બાયફોકલ લેન્સ - 7નીચે બે વિધાનો આપેલા છે :View Solution
વિધાન ($I$) : જ્યારે પદાર્થને એક અંતર્ગોળ લેન્સના વક્તાકેન્દ્ર આગળ મૂકવામાં આવે છે તો લેન્સની બીજી બાજુ, પ્રતિબિંબ વક્તાકેન્દ્ર ઉપર મળે છે.
વિધાન ($II$) : અંતર્ગોળ લેન્સ હંમેશા આભાસી અને સીધું પ્રતિબિંબ રચે છે.
ઉપરોક્ત વિધાનોનાં સંદભ્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 8$1.54$ વક્રીભવનાંક વાળા કાચમાંથી બનાવેલ $6^{\circ}$ કોણ ધરાવતા પાતળા પ્રિઝમ $P_1$ ને $1.72$ વક્રીભવનાંકવાળા કાચમાંથી બનાવેલ બીજા પ્રિઝમ $P_2$ સાથે જોડવામાં આવે છે કે જેથી સરેરાશ વિચલન સિવાય વિભાજન થાય. કોણ $P_2$ નો કોણ $.............{}^{\circ}$ હશે.View Solution
- 9એક બિંદુવત્ પદાર્થને એક કાચના સળિયો જેનો છેડો ગોળાકાર છે. તેની નજીક $O$ બિંદુએ મૂકેલ છે. આ ગાળાકારની વક્રતા ત્રિજ્યા $30 \,cm$ છે. તો રચાતું પ્રતિબિંબ .......છે.View Solution
- 10જ્યારે ક્રાઉન અને ફ્લીન્ટ ગ્લાસને અવર્ણક (achromatic) રીતે સંયોજીત કરી બનાવેલા પ્રિઝમમાં પીળા-કિરણ માટે $2^{\circ}$ જેટલું વિચલન મળે છે. ક્રાઉન અને ફ્લીન્ટ ગ્લાસ માટે ડીસ્પર્સીવ (dispersive) પાવર અનુક્રમે $0.02$ અને $0.03,$ અને પીળા પ્રકાશ માટે આ ગ્લાસો માટે વક્રીભવનાંક અનુક્રમે $1.5$ અને $1.6$ લો. ક્રાઉન ગ્લાસ માટે વક્રીભવન કોણ $........\,^{\circ}$ હશે. (નજીકત્તમ પૂર્ણાકમાં લખો)View Solution
