$1.5$ વક્રીભવનાંક વાળા $20\, cm$ જાડા કાચના સ્લેબને સમતલ અરીસાની સામે રાખેલ છે. એક વસ્તુને અરીસાથી $40\, cm$ અંતરે હવામાં રાખવામાં આવે છે. તો અરીસાની સાપેક્ષે પ્રતિબિંબનું સ્થાન ..... અંતરે હશે.
Diffcult
c
કાચના સ્લેબ માટે \( O\) બિંદુ વસ્તુ તરીકે કાર્ય કરે છે. અને અમુક અંતરે પ્રતિબિંબ રચાય છે.
કાચના સ્લેબ માટે \( O\) બિંદુ વસ્તુ તરીકે કાર્ય કરે છે. અને અમુક અંતરે પ્રતિબિંબ રચાય છે.
\(x\,\, = \,\,\,d\,\,\left[ {1 - \frac{1}{\mu }} \right]\,\,\, = \,\,\,20\,\,\left[ {1 - \frac{1}{{1.5}}} \right]\,\,\, = \,\,\,\frac{{20}}{3}\,\,cm\)
તેથી કાચનો સ્લેબ અરીસાને \(mm'\) થી \(MM\) તરફ ખસેડે છે. આ આભાસી સમતલ અરીસા પરથી વસ્તુનું અંતર
\( = \,\,40\,\, - \,\,x\,\, = \,\,40\,\, - \,\,\frac{{20}}{3}\,\, = \,\,\frac{{100}}{3}\,\,\,cm\)
આભાસી અરીસો \(mm'\) વાસ્તવિક અરીસા \(MM\) ની પાછળ \(100/3 \,\,cm\) અંતરે વસ્તુનું પ્રતિબિંબ રચશે.
\(mm'\) એ \(MM\) ની સામે \(20/3\,\, cm\) અંતરે હોય છે.
\(\therefore\) વાસ્તવિક સમતલ અરીસા \(MM\) પરથી પ્રતિબિંબનું અંતર \( = \,\,\frac{{100}}{3}\,\, - \,\,\frac{{20}}{3}\,\,\, = \,\,\frac{{80}}{3}\,\,cm\)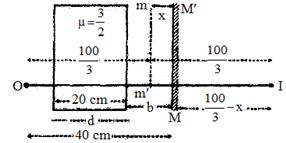
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$40\;cm$ કેન્દ્રલંબાઇ ધરાવતા બે સમતલ બર્હિગોળ લેન્સને એકબીજા સાથે જોડીને તેમાંથી બર્હિગોળ લેન્સ બનાવવામાં આવે છે. તેના દ્વારા વાસ્તવિક, ઊંધું અને એક મોટવણી મેળવવા માટે કેટલા.........$cm$ ના અંતરે વસ્તુ મૂકવી જોઇએ?View Solution
- 2ટેલિસ્કોપનો મેગ્નિફિકેશન પાવર $9$ અને લેન્સ વચ્ચેનું અંતર $20\, cm$ છે તો ઘટક લેન્સની કેન્દ્રલંબાઈ શું થશે?View Solution
- 3એક્રોમેટિક અપસારી લેન્સની કેન્દ્રલંબાઈ $20\,cm$ છે. તે $1:2$ વિભેદન પવારનો ગુણોતર ધરાવતા દ્રવ્યમાથી બનાવેલ છે. તેમની કેન્દ્રલંબાઈ $f_1$ અને $f_2$ છે. તોView Solution
- 4'$d$' ઊંડાઈના પાત્રમાં અડધે સુધી $n _1$ વક્રીભવનાંક ધરાવતું તેલ, અને બાકીનો અડધો ભાગ $n _2$ વક્રીભવનાંક ધરાવતા પાણીથી ભરવામાં આવે છે.જ્યારે આા પાત્રમાં ઉપરથી જોતાં તેની દેખાતી ઊંડાઈ $.........$ થશે.View Solution
- 5સૂર્યનો વ્યાસ $1.4 \times {10^9}\,m$ અને સૂર્યનું પૃથ્વીથી અંતર ${10^{11}}\,m$ છે.$2\,m$ કેન્દ્રલંબાઇ ધરાવતા બર્હિગોળ લેન્સથી પ્રતિબિંબનો વ્યાસ કેટલા .....$cm$ મળે?View Solution
- 6એક પેપરને પાણી ભરેલા ગ્લાસની નીચે મૂકવામાં આવે છે. જ્યાં પાણી અને ગ્લાસનો વક્રીભવનાંક અનુક્રમે $1.5$ અને $1.33$ છે. જો ગ્લાસના તળિયાની જાડાઈ $1\, cm$ અને ભરેલા પાણીની ઊંડાઈ $5\, cm$ હોય તો ઉપરથી જોતાં કાગળ કેટલું શીફ્ટ થયેલું દેખાશે?View Solution
- 7માધ્યમમાં પ્રકાશનો વેગ $1.5 \times {10^8}m/s$ ,હોય તો માધ્યમનો વક્રીભવનાંક કેટલો હશે?View Solution
- 8$P$ બિંદુ એ પ્રકાશ કિરણ પુંજ અભિકેન્દ્રીત થાય છે. $P$ બિંદુથી $12\,\, cm$ પ્રકાશ પુંજના પથ પર એક લેન્સ મૂકવામાં આવે છે. જો લેન્સ $16\,\, cm$ કેન્દ્રલંબાઈ ધરાવતો અંતર્ગોળ કાચ હોય, તો ક્યાં......$cm$ બિંદુએ કિરણપુંજ અભિકેન્દ્રિત થાય?View Solution
- 9$2R\, cm$ વ્યાસ ધરાવતી નળાકાર પાણીની ટાકીમાંથી પાણી સમાન દરથી બહાર નીકળે ત્યારે આભાસી ઊંડાઈ $x \,cm/minute$ ના દરથી ઘટે છે. તો એક મિનિટ માં બહાર નીકળતા પાણીની માત્રા .......... $c.c.$View Solution
($n_1=$ હવાનો વક્રીભવનાંક)
($n_2=$ પાણીનો વક્રીભવનાંક)
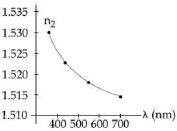
- 10ક્રાઉન ગ્લાસના પાતળા પ્રિઝમના વક્રીભવનાંક્નો આપાત પ્રકાશની તરંગલંબાઈ સાથેનો સંબંધ દર્શાવેલ છે. જો $ D_m$ એ લઘુત્તમ વિચલન છે, તો નીચેમાંથી ક્યો આલેખ સાચો છે?View Solution