$2\; kg$ દ્રવ્યમાન અને $4\; cm$ ત્રિજ્યા ધરાવતો એક ઘન નળાકાર તેની અક્ષની સાપેક્ષે $3\; rpm$ ના દરથી ભ્રમણ કરે છે. $2\pi $ ભ્રમણ પછી તેને રોકવા માટે કેટલા ટોર્કની જરૂર પડશે?
NEET 2019, Diffcult
a
\(\theta= 2 \pi\) radian
\(\theta= 2 \pi\) radian
\(\omega_{0}=3 \mathrm{rpm} \Rightarrow \frac{2 \pi}{60}(3) \frac{\mathrm{rad}}{\mathrm{sec}}\)
\(\omega^{2}=\omega_{0}^{2}-2 \alpha \theta\)
\(0=\left(\frac{3 \times 2 \pi}{60}\right)^{2}-2 \alpha\left(4 \pi^{2}\right)\)
\(\therefore \alpha=\frac{1}{800} \mathrm{rad} / \mathrm{s}^{2}\)
\(\tau=\frac{m R^{2}}{2} \alpha=\frac{2}{2} \times\left(\frac{4}{100}\right)^{2} \times \frac{1}{800}=2 \times 10^{-6} \mathrm{Nm}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
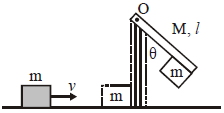
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $m =1\, kg$ દળનો એક પદાર્થ $v=6\, m / s$ જેટલા વેગથી એક ઘર્ષણરહિત સપાટી પર ગતિ કરીને એક સળિયા સાથે અથડાયને તેની સાથે જોડાય જાય છે. આ સળિયો $O$ બિંદુ સાથે જડેલ છે અને અથડામણના કારણે તે $\theta$ ખૂણો બનાવે છે. જો સળિયાનું દળ $M =2 \,kg $ અને લંબાઈ $l=1\, m $ હોય તો $\theta$ ખૂણાનું મૂલ્ય કેટલું હશે?View Solution
$(\left.g=10 \,m / s ^{2}\right)$
- 2$5 \mathrm{~kg}$ દળ ધરાવતો પદાર્થ $3 \sqrt{2} \mathrm{~ms}^{-1}$ ની સમાન ઝડપ સાથે $X-Y$ સમતલમાં $y=x+4$ રેખાની દિશામાં ગતિ કરે છે. ઉગમબિંદુને અનુલક્ષીને કણનું કોણીય વેગમાન__________$\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-1}$ થશે.View Solution
- 3View Solutionએક પાતળી સમક્ષિતિજ તકતી તેના કેન્દ્રમાંથી પસાર થતી શિરોલંબ અક્ષને અનુલક્ષીને ચાકગતિ કરે છે. એક જંતુ એ તકતીના વ્યાસ પર એક છેડેથી સામેના બીજા છેડે ગતિ કરે છે. તો તેની ગતિ દરમિયાન તકતીની કોણીય ઝડપ.....
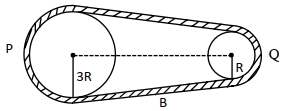
- 4આપેલ આકૃતિમાં બે પૈડાં $P$ અને $Q$ ને બેલ્ટ $B$ થી જોડવામાં આવેલ છે. $P$ પૈડાની ત્રિજયા $Q$ પૈડાં કરતાં ત્રણ ગણી છે. સમાન ચાકગતિઊર્જાના કિસ્સામાં તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર $\left(\frac{{I}_{1}}{{I}_{2}}\right)$, ${x}: 1$ હોય તો ${x}$ નું મુલ્ય કેટલું હશે?View Solution
- 5જો $\mathop \omega \limits^ \to \,\, = \,\,(3\,\hat i\,\, + \,\,4\hat j\,\, + \,\,5\hat k)\,\,\,rad/s$ અને $\mathop r\limits^ \to \,\, = \,\,(\hat i - 2\hat j + 3\hat k)\,m$ હોય, તો પદાર્થના રેખીય વેગનો સદિશ .......View Solution
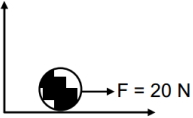
- 6આપેલ આકૃતિ માટે દ્રવ્યમાન કેન્દ્રનો પ્રવેગ અને કોણીય પ્રવેગનો ગુણોતર કેટલો થાય? $m =2\;kg$ અને $r =10\;cm$ છે.View Solution
- 7એક પાતળા સળિયાને તેના કેન્દ્રમાંથી પસાર થતી અને સળિયાને લંબ તેવી અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્ર $2400 \mathrm{~g} \mathrm{~cm}^2$ છે. સળિયાની લંબાઈ લગભગ. . . . . થશે. સળિયાનું દળ $400 \mathrm{~g}$ છે.View Solution
- 8$a$ બાજુવાળા ચોરસના ચાર ખૂણા $P, Q, R$ અને $S$ પર અનુક્રમે $1\ kg, 1\ kg, 2 \ kg$ અને $2\ kg$ મુકેલ છે, તો તંત્રનું દ્રવ્યમાન કેન્દ્ર કોનાથી સૌથી દૂર હશે ?View Solution
- 9દળમાં ફેરફાર વગર જો પૃથ્વીની ત્રિજ્યા તેના વર્તમાન મૂલ્ય કરતાં $n$ ગણી થઈ જાય તો દિવસનો સમયગાળો કેટલો છે ?View Solution
- 10એક વર્તૂળાકાર તકતી $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. જો તકતી પર બાળક બેસે, તો શેનું સંરક્ષણ થશે ?View Solution
