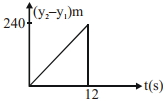
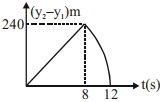
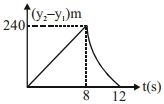
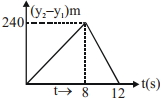
$240\;m$ ઊંચા ખડકની ટોચ પરથી બે પથ્થરને અનુક્રમે $10\;ms^{-1}$ અને $40\;ms^{-1}$ ની પ્રારંભિક ઝડપથી ઊર્ધ્વ દિશામાં ફેંકવામાં આવે છે. નીચે દર્શાવેલ આલેખો પૈકી કયો આલેખ બીજા પથ્થરનો પ્રથમ પથ્થરની સખામણીમાં સાપેક્ષ-સ્થાનનો સમય સાથેનો ફેરફાર સૌથી સારી રીતે રજૂ કરે છે?
(ધારો કે પથ્થરો જમીન પરથી અથડાઇને પાછો ફેંકાતો નથી અને હવાનો અવરોધ અવગણો, $g=10$ $ms^{-2}$ લો.)
(અત્રે આકૃતિઓ ફકત રેખાકૃતિ સૂચવે છે, તેઓ એક જ સ્કેલ પર દોરેલ નથી.)
- A
- B
- C
- D
JEE MAIN 2015, Medium
Download our app for free and get started
c
\(\begin{array}{l}
{y_1} = 10t - 5{t^2};{y_2} = 40t - 5{t^2}\\
for\,\,\,\,\,{y_1} = - 240m,t = 8s\\
\therefore \,\,\,\,\,\,\,\,\,\,{y_2} - {y_1} = 30t\,for\,t \le 8s.\\
for\,\,\,\,\,\,t > 8s.\\
{y_2} - {y_1} = 240 - 40t - \frac{1}{2}g{t^2}
\end{array}\)
\(\begin{array}{l}
{y_1} = 10t - 5{t^2};{y_2} = 40t - 5{t^2}\\
for\,\,\,\,\,{y_1} = - 240m,t = 8s\\
\therefore \,\,\,\,\,\,\,\,\,\,{y_2} - {y_1} = 30t\,for\,t \le 8s.\\
for\,\,\,\,\,\,t > 8s.\\
{y_2} - {y_1} = 240 - 40t - \frac{1}{2}g{t^2}
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
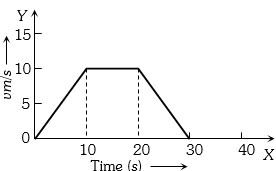
- 1આપેલ ગ્રાફ માટે પદાર્થે કાપેલ અંતર .......... $\mathrm{m}$ હશે.View Solution
- 2એક કાર $X$ સ્થાનથી $Y$ સ્થાન સુધી અચળ ઝડપ $v_1$ અને પાછી $X$ સ્થાને અચળ ઝડપ $v_2$ થી આવે છે. તેની આ મુસાફરી દરમિયાનની સરેરાશ ઝડપ કેટલી થાય?View Solution
- 3એ કે કાર સુરેખ રેખા પર ગતિ કરે છે. જેમકે આકૃતિમાં $OP$. આ કાર $18\; s$ માં $O$ થી $P$ જાય છે અને $6\; s$ માં $P$ થી $Q$ પરત જાય છે. કાર $O$ થી $P$ પર જઈ $Q$ પર પાછી ફરે, ત્યારે તેનો સરેરાશ વેગ અને સરેરાશ ઝડપ શું હશે ?View Solution
- 4કણ ઘન $+x-$ દિશામાં $5\, m$ અંતર કાપે તો તેનું સ્થાનાંતર મેળવો.View Solution
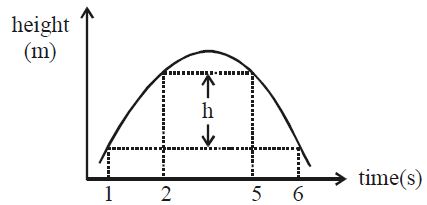
- 5એક દડાને ઉપર તરફ ફેંકવામાં આવે છે. તેની ઊંચાઈ નીચે મુજબ સમય સાથે બદલાય છે. ગુરુત્વ પ્રવેગ $7.5\ m/s^2$ હોય તો ઊંચાઈ $h$ એ કેટલા $..........m$ હશે?View Solution
- 6ચલ બળની અસર હેઠળ એક કણ એક પરિમાણમાં ( $x$ અક્ષ પર) ગતિ કરે છે. તેનું પ્રારંભિક સ્થાન ઉગમબિંદ્દુની જમણી બાજુ $16 \mathrm{~m}$ પર છે. તેના સ્થાનનો સમય $(\mathrm{t})$ સાથેનો ફેરફાર $(x), x=-3 \mathrm{t}^3+18 \mathrm{t}^2+16 \mathrm{t}$, જ્યા જ્યા $x$ mમાં અને $\mathrm{t}$ સેકન્ડમાં છે, મુજબ દર્શાવવામા આવે છે. જ્યારે તેને પ્રવેશ શૂન્ય થાય તે વખતે તેનો વેગ_________$\mathrm{m} / \mathrm{s}$. હશે.View Solution
- 7બે કાર $A$ અને $B$ શરૂઆતમાં સ્થિર છે. જો કાર $A$ $40\, m/sec$ ના અચળ વેગથી અને $B$ સમાન દિશામાં $4\,m/{s^2}$ ના પ્રવેગથી ગતિની શરૂઆત કરે તો કાર $B $ કાર $A$ ને કેટલા સમય($sec$ માં) પછી પકડી શકે?View Solution
- 8એક પદાર્થ સ્થિર સ્થિતી થી શરૂ થાય છે અને $x$-અક્ષની સાપેક્ષ ગતિ કરે છે જેથી કોઈપણ તત્કાલમાં તેનું સ્થાન $x=4 t^2-12 t$ હોય છે જ્યાં $t$ સેકંડમાં અને $v \,m / s$ માં હોય છે. પદાર્થનો પ્રવેગ કેટલો થાય?View Solution
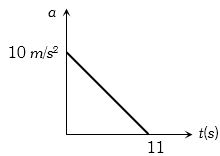
- 9સ્થિર સ્થિતિમાંથી ગતિ કરતાં પદાર્થનો પ્રવેગ વિરુધ્ધ સમયનો આલેખ આપેલ છે.તો પદાર્થની મહત્તમ ઝડપ કેટલી ......$m/s$ થશે?View Solution
- 10એક પદાર્થનો વેગ એ $v=\frac{t^2}{10}+20$ સમીકરણના આધારે સમય પર આધાર રાખે છે. પદાર્થ નીચેમાંથી ક્યાં પ્રકારની ગતિ કરે છે ?View Solution