$2.5$ $E_v$ બૅન્ડગેપ ધરાવતા દ્રવ્યમાંથી ફોટો-ડાયોડ બનાવેલ છે. તે કઈ તરંગલંબાઈના વિકિરણને પારખી શકશે ?
Medium
c
\(Eg = 2.5 eV = 2.5 × 1.6× 10^{-19}J\)
\(Eg = 2.5 eV = 2.5 × 1.6× 10^{-19}J\)
હવે, \({E_g} = \,\,\,\frac{{hc}}{\lambda }\,\,\,\,\)
\(\therefore \,\,\,\lambda \,\, = \,\,\frac{{hc}}{{{E_g}}}\,\, = \,\,\frac{{6.62\,\, \times \,\,{{10}^{ - 34}} \times \,3\,\, \times \,\,{{10}^8}}}{{2.5\,\, \times \,\,1.6\,\, \times \,\,{{10}^{ - 19}}}}\,\,\, = \,\,4.965\,\, \times \,\,{10^{ - 7}}\,m\,\, = \,\,4965\,\,\mathop A\limits^ \circ \)
એટલે કે ફોટો-ડાયોડ \(4000 Å\) તરંગલંબાઈ ધરાવતા વિકિરણને પારખી શકશે.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જયારે $P-N$ જંકશન ફોરવર્ડ બાયસમાં હોય ત્યારે પોટેન્શિયલ બેરિયરની પહોળાઈView Solution
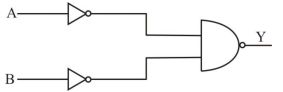
- 2નીચે દર્શાવેલ લોજિક પરિપથ માટે તમામ સંભવિત $A$ અને $B$ મૂલ્યો માટે $Y$ આઉટપુટને કયા ટુથટેબલ વડે દર્શાવી શકાય છે?View Solution
- 3અર્ધતરંગ રેક્ટિફાયર $1 K$ $\Omega$ નો ભાર વિદ્યુત પ્રવાહ આપે છે. વોલ્ટેજ $220V $ છે, ડાયોડના પ્રતિરોધકને અવગણતા, રિપલ વોલ્ટેજ $(rms)$ ની કિંમત ....$volt$ છે.View Solution
- 4કોઈ એક $p-$ પ્રકારના અર્ધવાહક માટે નીચેમાંથી કયું વિધાન સાચું છે?View Solution
- 5અર્ધવાહકોમાં ઊર્જાગેપને ........$eV$ માં ક્રમની હોય છે.View Solution
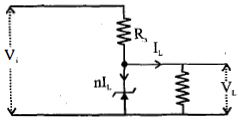
- 6આપેલ $dc$ સ્ત્રોત ધરાવતા પરિપથમાં અવરોધ $R_S$ નું મૂલ્ય કેટલું હશે?View Solution
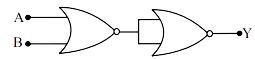
- 7View Solutionનીચે દર્શાવેલ લોજીક પરિપથને સમતુલ્ય લોજીક ગેટ જણુાવો.
- 8View Solutionનીચેનામાંથી અમોરફસ પદાર્થ કયો છે.
- 9શુદ્ધ સેમિકંડક્ટરમાં ઇલેક્ટ્રોન અને દોલનોની સંખ્યા ઘનતા $10^{16} m ^{-3}$ છે. ગેલિયમ ઉમેરતા $n _{ h }=5 \times 10^{22} m ^{-3}$ થાય તો, $n _{ e } = ......$View Solution
- 10View Solutionનીચેનામાંથી ઘન પદાર્થમાં કયો નબળો બંધ છે.
