$2.5 \,m$ ત્રિજયામાં દોરી સાથે બાંધેલો પદાર્થ અચળ ઝડપથી પરિભ્રમણ કરે છે.દોરીમાં મહત્તમ અને ન્યુનત્તમ તણાવનો ગુણોત્તર $5:3$ હોય ,તો પદાર્થની ઝડપ કેટલી હશે?
Diffcult
a
(a) In this problem it is assumed that particle although moving in a vertical loop but its speed remain constant.
(a) In this problem it is assumed that particle although moving in a vertical loop but its speed remain constant.
Tension at lowest point \({T_{\max }} = \frac{{m{v^2}}}{r} + mg\)
Tension at highest point \({T_{\min }} = \frac{{m{v^2}}}{r} - mg\)
\(\frac{{{T_{\max }}}}{{{T_{\min }}}} = \frac{{\frac{{m{v^2}}}{r} + mg}}{{\frac{{m{v^2}}}{r} - mg}} = \frac{5}{3}\)
by solving we get,\(v = \sqrt {4gr} \)\( = \sqrt {4 \times 9.8 \times 2.5} \)\( = \sqrt {98} \,m/s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $m_1$ દળનો કણ $v_1 $ વેગ સાથે ગતિ કરે છે અને બીજો $m_2$ દળનો કણ $V_2$ વેગ સાથે ગતિ કરે છે. તે બંનેનું વેગમાન સમાન છે પરંતુ તેમની જુદી જુદી ગતિ ઊર્જા અનુક્રમે $E_1$ અને $E_2$ છે. જો $m_1$ > $m_2$ હોય તો.......View Solution
- 2એક સાદું લોલક લાકડાનાં $50 \,g$ દળ ધરાવતા દોલક અને $2 \,m$ લંબાઈનું બનેલું છે. $75 \,g$ દળ ધરાવતી બુલેટ (ગોળી) ને $v$ જેટલા વેગથી લોલક તરફ ફાયર કરવામાં આવે છે. ગોળી દોલકમાંથી $\frac{v}{3}$ જેટલી ઝડપ સાથે બહાર આવે છે અને દોલક એક ઉર્ધ્વ (શિરોલંબ) વર્તુળ પૂર્ણ કરે છે. તો $v$ નું મૂલ્ય ............ $ms ^{-1}$ થશે. ( $g =10 \,m / s ^{2}$ લો.)View Solution
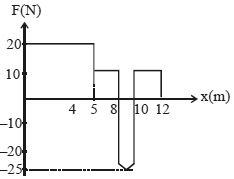
- 3સ્થિર રહેલ $500\; \mathrm{g}$ દળના પદાર્થ પર બદલાતું બળ લગતા તેનો $\mathrm{X}$ ઘટક નીચે દર્શાવ્યા પ્રમાણે બદલાય છે. તો $X=8 \;\mathrm{m}$ અને $X=12\; \mathrm{m}$ બિંદુ આગળ કણનો વેગ કેટલો થાય?View Solution
- 4$75 \%$ કાર્યક્ષમતા ધરાવતા મશીન દ્વારા $1 kg$ના પદાર્થને અમુક ઊંચાઇ પર લઇ જતાં $12 J$ ઊર્જા વપરાય છે.જો પદાર્થને મુકત કરવામાં આવે,તો જમીન પર વેગ કેટલો થશે? ( $ m{s^{ - 1}}) $View Solution
- 5પદાર્થ પર $ \vec F = (5\hat i + 3\hat j + 2\hat k)N $ બળ લાગતાં તે ઉદ્ગમબિંદુથી $ \vec r = (2\hat i - \hat j)m $ ખસે તો કેટલું કાર્ય થતું હશે?View Solution
- 6$m_1$ દળવાળો કણ $v_1$ વેગથી અને $m_2$ દળવાળો કણ $v_2$ વેગથી ગતિ છે. બંનેના વેગમાન સમાન છે પરંતુ તેની જુદી-જુદી ગતિઊર્જા અનુક્રમે $E_1$ અને $E_2$ છે. જો $m_1 > m_2$ હોય, તો ............View Solution
- 7ગોળી લાકડાના બ્લોકમાંથી પસાર થતા $ 20$ માં ભાગનો વેગ ગુમાવે છે.તો ગોળીને સ્થિર કરવાં કેટલા લઘુત્તમ બ્લોકની જરૂર પડશે?View Solution
- 8$m $ દળનું એક વાહન સ્થિર સ્થિતિએથી પ્રવેગીત થાય છે. જો એન્જિન $p$ જેટલો અચળ પાવર અપાતુ હોય તો $(s)$ સમયે વાહનનું $(t) $ સ્થાન કયા સૂત્રથી આપી શકાય?View Solution
- 9$1\, m$ લંબાઇ અને ${60^o}$ ખૂણાવાળા ઢાળ પર $1\, kg$ નો બ્લોક મૂકતાં ઘર્ષણ વિરુધ્ધ ...... $J$ કાર્ય થશે. (ગતિક ઘર્ષણાંક $0.5$ છે)View Solution
- 10$1\, m$ ઊંચાઈ ધરાવતા ટેબલ પર એક $1.9\, kg$ દળનો બ્લોક પડેલો છે. $0.1\, kg$ ધરાવતી ગોળી આ બ્લોક સાથે અથડાય અને તેની સાથે જોડાઈ જાય છે. જો અથડાતાં પહેલા આ ગોળીનો સમક્ષિતિજ દિશામાં વેગ $20\, m / s$ હોય તો પછી બ્લોક જ્યારે જમીન સાથે અથડાય તેની પહેલા આ જોડાયેલા તંત્રની ગતિઉર્જા કેટલા $J$ હશે?View Solution
$[g =10\, m / s ^{2}$. ધારો કે તેમાં કોઈ ચાક ગતિ નથી અને અથડામણ પછી ઉર્જાનો વ્યય નહિવત છે.$]$
