\(v=\frac{V_{a v}}{\lambda}\)
\(\lambda=\frac{\mathrm{RT}}{\sqrt{2} \pi \sigma^{2} \mathrm{N}_{\mathrm{A}} \mathrm{P}}\)
\(\sigma=2 \times 0.3 \times 10^{-9}\)
\(P=\frac{R T}{V}\)
\(\Rightarrow \quad=\frac{V}{\sqrt{2} \pi \sigma^{2} N_{A}}\)
\(V_{\mathrm{av}}=\sqrt{\frac{8}{3 \pi}} \times V_{\mathrm{rms}}\)
\(\begin{aligned} \therefore \quad \mathrm{v} =\frac{200 \times \sqrt{2} \pi \times \sigma^{2} \mathrm{N}_{\mathrm{A}}}{25 \times 10^{-3}} \times \sqrt{\frac{8}{3 \pi}} \\ =17.68 \times 10^{8} / \mathrm{sec} \\ =0.1768 \times 10^{10} / \mathrm{sec}-10^{10} \end{aligned}\)
This answer does not match with JEE - Answer key
Download our appand get started for free
Similar Questions
- 1અચળ દબાણે એક આદર્શ વાયુનું $27°C$ તાપમાને કદ $V$ હોય તો તાપમાન વધારીને $327°C$ કરતા તેનું અંતિમ કદ ......View Solution
- 2સમાન વાયુને સમાન કદ અને સમાન તાપમાન ધરાવતા બે પાત્રોમાં ભરવામાં આવે છે. જો અણુઓની સંખ્યાનો ગુણોત્તર $1:4$ હોય તો ....................View Solution
$A$. વાયુ અણુઓ માટે બંને પાત્રોમાં $r.m.s.$ વેગ સમાન હશે
$B$.આ પાત્રોમાં દબાણનો ગુણોત્તર $1:4$ હશે
$C$. દબાણનો ગુણોત્તર $1: 1$ છે
$D$. વાયુ અણુઓ માટે બંને પાત્રોમાં $r.m.s.$ વેગનો ગુણોત્તર $1:4$ હશે
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 3હાઇડ્રોજન વાયુ માટે ${C_p} - {C_v} = a$ અને ઓક્સિજન વાયુ માટે ${C_p} - {C_v} = b$ હોય તો $a$ અને $b$ વચ્ચેનો સંબંધ શું હશે?View Solution
- 4જો આપેલ તાપમાને અને દબાણ હાઈડ્રોજન પરમાણુ માટેનો સરેરાશ વર્ગિત વર્ગ વેગ $2 \mathrm{~km} / \mathrm{s}$ હોય તો આ જ સ્થિમાં રહેલ ઓક્સિનન માટે સરેરાશ વર્ગિત વર્ગ વેગ $km/s$ માં__________હશે.View Solution
- 5$T _{1}, T _{2}$ અને $T _{3}$ તાપમાને રહેલાં ત્રણ આદર્શ વાયુઓનું મિશ્રણ કરવામાં આવે છે. તેમનાં અણુભાર $m _{1}, m _{2}$ અને $m _{3}$ છે. તથા અણુુ ઓની સંખ્યા $n _{1}, n _{2}$ અને $n _{3}$ છે. ઊર્જાનો કોઇ વ્યય થતો નથી તેમ ધારતા, મિશ્રણનું તાપમાન કેટલું થાય?View Solution
- 6હાઇડ્રોજન વાયુ માટે ${C_p} - {C_v} = a$ અને ઓક્સિજન વાયુ માટે ${C_p} - {C_v} = b$ હોય તો $a$ અને $b$ વચ્ચેનો સંબંધ શું હશે?View Solution
- 7$10^o C$ જેટલા તાપમાને નિશ્ચિત દ્રવ્યમાન ધરાવતા આદર્શવાયુની ઘનતાને દબાણ વડે ભાગતા $x$ મળે છે. $ 110^o C $ તાપમાને આ ગુણોત્તર કેટલો હશે?View Solution
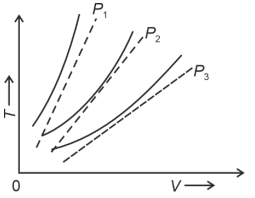
- 8ત્રણ દબાણ $P_1, P_2$ અને $P_3$ એ નીચે દર્શાવેલ આલેખ એક આદર્શ વાયુનો $T-V$ વક્ર (જ્યાં $T$ એ તાપમાન અને $V$ એ કદ છે) ચાર્લ્સના નિયમ જેને ત્રૂટક રેખાથી દર્શાવેલ છે, તેની સાથે સરખાવેલ છે. તો સાચો સંબંધ. . . . . . છે.View Solution
- 9$20°C$ તાપમાને વાયુનું કદ $200\, ml$ છે.અચળ દબાણે તાપમાન $-20°C$ કરવામાં આવે,તો નવું કદ ....... $ml$ થાય?View Solution
- 10$27°C$ તાપમાને વાયુનું કદ $V$ અને દબાણ $P$ છે. તેને ગરમ કરતાં દબાણ બમણું અને કદ ત્રણ ગણું થાય છે, તો અંતિમ તાપમાન ...... $^oC$ કેટલું $?$View Solution
