$283\,V$ ના $Peak\,Value$ અને $50\,H _{ z }$ આવૃત્તિનl $Sinusoidal$ વોલ્ટેજ ને શ્રેણી $LCR$ પરિપથમાં લાગેવલ છે. જેમાં $R =3\; \Omega, L =25.48\,mH$ અને $C =796\; \mu F$ છે. પરિપથમાં ઈમ્પીડન્સ $............\Omega$
Easy
Download our app for free and get started
a
(a)
(a)
\(X_L=2 \pi f L\)
\(=2 \times 3.14 \times 50 \times 25.48 \times 10^{-3} \Omega=8 \Omega\)
\(X_C=\frac{1}{2 \pi f fC }=\frac{1}{2 \times 3.14 \times 50 \times 796 \times 10^{-6}}=4 \Omega\)
Therefore,
\(Z =\sqrt{ R ^2+\left( X _{ L }- X _{ C }\right)^2}=\sqrt{3^2+(8-4)^2}=5 \Omega\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1લિસ્ટ $-I$ ને લિસ્ટ $-II$ સાથે યોગ્ય રીતે જોડો.View Solution
લિસ્ટ $-I$ લિસ્ટ $-II$ $(a)$ માત્ર અવરોધ ધરાવતા $AC$ પરિપથમાં પ્રવાહ અને વૉલ્ટેજ વચ્ચેનો કળા તફાવત $(i)$ પ્રવાહ એ વૉલ્ટેજ કરતાં કળામાં $\frac{\pi}{2}$ જેટલો આગળ હોય $(b)$ માત્ર ઇન્ડક્ટર ધરાવતા $AC$ પરિપથમાં પ્રવાહ અને વૉલ્ટેજ વચ્ચેનો કળા તફાવત $(ii)$ શૂન્ય $(c)$ માત્ર કેપેસીટર ધરાવતા $AC$ પરિપથમાં પ્રવાહ અને વૉલ્ટેજ વચ્ચેનો કળા તફાવત $(iii)$ પ્રવાહ એ વૉલ્ટેજ કરતાં કળામાં $\frac{\pi}{2}$ જેટલો પાછળ હોય $(d)$ $LCR$ શ્રેણી પરિપથમાં પ્રવાહ અને વૉલ્ટેજ વચ્ચેનો કળા તફાવત $(iv)$ $\tan ^{-1}\left(\frac{X_{C}-X_{L}}{R}\right)$ - 2નીચે બે વિધાનો આપેલા છે:View Solution
વિધાન $I$ : $LCR$ શ્રેણી પરિપથમાં, અનુનાદ વખતે મહત્તમ પ્રવાહ મળે છે.
વિધાન $II$ : જ્યારે બંનેને સમાન વોલ્ટેજ ઉદ્રગમ સાથે જોડેલા હોય ત્યારે ફક્ત અવરોધ ધરાવતા પરિપથ માં $LCR$ પરિપથ કરતાં કદાપી ઓછl પ્રવાહ મળશે નહી.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીયે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરોઃ
- 3એક શ્રેણી $L C R$ પરિપથમાં $10\,mH$ નો ઇન્ડકટન્સ $L, 1\,\mu F$ નો સંધારક $C$ અને $100\,\Omega$ નો અવરોધ $R$ છે. તો અનુનાદ ઉદભવે તે વખતે આવૃત્તિ $.......$ છે.View Solution
- 4એસી પરિપથમાં પાવર ફેકટર $\frac{1}{3}$ થી $\frac{1}{9}$ બદલાય છે, તો જો અવરોધ અચળ રહે તો રિએેકટન્સ કેટલી ટકાવારીથી બદલાશે (અંદાજિત)View Solution
- 5પ્રમાણભૂત ફિલામેન્ટ લેમ્પ $100\,W$ વાપરે છે, જ્યારે તેને $200\,V$ ના $ac$ મુખ્ય સપ્લાય સાથે જોડવામાં આવે. બલ્બમાંથી પસાર થતો મહત્તમ પ્રવાહ $........\,A$ હશેView Solution
- 6$\mathrm{L}=\frac{100}{\pi} \mathrm{mH}, \mathrm{C}=\frac{10^{-3}}{\pi} \mathrm{F}$ અને $\mathrm{R}=10 \Omega$ ધરાવતો એક શ્રેણી $LCR$ પરિપથ, $220 \mathrm{~V}, 50 \mathrm{~Hz}$ $A.C$. ઉદગમ સાથે જોડવામાં આવે છે. પરિપથનો પાવર ફેકટર_______થશે.View Solution
- 7$LCR$ શ્રેણી પરિપથમાં અનુનાદ સમયે પરિપથમાં થતો પવારનો વ્યય કેટલો હોય?View Solution
- 8$A.C$. પરિપથમાં, વોલ્ટેજ અને પ્રવાહ અનુક્રમેView Solution
$\mathrm{V}=100 \sin (100 \mathrm{t}) \mathrm{V}$અને
$\mathrm{I}=100 \sin \left(100 \mathrm{t}+\frac{\pi}{3}\right) \mathrm{mA} $ { વડે આપવામાં આવે છે, }
પરિપથમાં વિખેરીત થતો પાવર (કાર્યત્વરા)_______થશે.
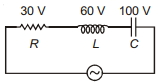
- 9View Solutionનીચે (આકૃતિમાં દર્શાવ્યા અનુસાર) જણાવેલ પરિપથ માટે ઉચ્ચત્તમ (મહત્તમ) પ્રવાહ અને અનુનાદિત આવૃત્તિ શોધો.
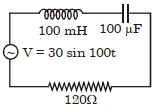
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $R L C$ શ્રેણી પરિપથમાં $R, L$ અને $C$ માં $30\,V , 60\,V$ અને $100\,V$ છે.સ્ત્રોતનો $r mf$ (વોલ્ટમાં) કેટલો છે ?View Solution
