$3\; kg $ નો ઘન નળાકાર $4 \;m/s $ ના વેગથી સમક્ષિતિજ સપાટી પર ગબડે છે. તે $200\; N/m $ બળઅચળાંક ધરાવતી સમક્ષિતિજ સ્પિંગ્ર સાથે અથડાય છે. સ્પિંગનું મહતમ સંકોચન ($m$ માં) કેટલું થાય?
AIPMT 2012, Diffcult
b
\(\begin{array}{l}
\,\,\,\,\,\,\,\,\,\,\,At\,{\rm{maximum}}\,compression\,the\\
solid\,cylinder\,will\,stop.\\
According\,to\,law\,of\,conservation\,of\,\\
mechanical\,energy\\
Loss\,in\,kinetic\,energy\, = Gain\,in\,potential\\
energy\,of\,cylinder\,of\,spring\\
\frac{1}{2}m{v^2} + \frac{1}{2}I{\omega ^2} = \frac{1}{2}k{x^2}\\
\frac{1}{2}m{v^2} + \frac{1}{2}\left( {\frac{{m{R^2}}}{2}} \right){\left( {\frac{v}{R}} \right)^2} = \frac{1}{2}k{x^2}
\end{array}\)
\(\begin{array}{l}
\,\,\,\,\,\,\,\,\,\,\,At\,{\rm{maximum}}\,compression\,the\\
solid\,cylinder\,will\,stop.\\
According\,to\,law\,of\,conservation\,of\,\\
mechanical\,energy\\
Loss\,in\,kinetic\,energy\, = Gain\,in\,potential\\
energy\,of\,cylinder\,of\,spring\\
\frac{1}{2}m{v^2} + \frac{1}{2}I{\omega ^2} = \frac{1}{2}k{x^2}\\
\frac{1}{2}m{v^2} + \frac{1}{2}\left( {\frac{{m{R^2}}}{2}} \right){\left( {\frac{v}{R}} \right)^2} = \frac{1}{2}k{x^2}
\end{array}\)
\(\begin{array}{l}
\,\,\,\,\,\,\,(v = R\omega \,and\,for\,solid\,cylinder,\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,I = \frac{1}{2}m{R^2})\\
\frac{1}{2}m{v^2} = \frac{1}{4}m{v^2} = \frac{1}{2}k{x^2}\\
\frac{3}{4}m{v^2} = \frac{1}{2}k{x^2}\,or\,{x^2} = \frac{3}{2}\,\frac{{m{v^2}}}{k}\\
Here,\,m = 3\,kg,\,v = 4\,m\,{s^{ - 1}},\,k = 200\,N\,{m^{ - 1}}\\
Subsitituting\,the\,given\,values,\,we\,get\\
{x^2} = \frac{{3 \times 3 \times 4 \times 4}}{{2 \times 200}} \Rightarrow {x^2} = \frac{{36}}{{100}}\,or\,x = 0.6\,m
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કોઈ સમક્ષિતિજ સમતલ તેના કેન્દ્રમાથી પસાર થતી શિરોલંબ અક્ષને અનુલક્ષીને નિયમિત કોણીય વેગથી ભ્રમણ કરે છે. કોઈ ક્ષણે $m$ દળના ઘટ્ટ પ્રવાહીને તેના કેન્દ્ર પર પાડતા તે ફેલાઈને નીચે પડે છે. આ દરમિયાન તેનો કોણીય વેગમાં શું થશે?View Solution
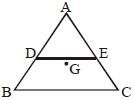
- 2$ABC$ સમબાજુ ત્રિકોણ તકતી છે.$O$ અને $E$ એ $AB$ અને $AC$ના મધ્યબિંદુ છે.$G$ એ કેન્દ્ર છે. $G$ માંથી પસાર થતી અને સમતલ $ABC$ને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા $I _{0}$ છે.જો $ADE$ ભાગને દૂર કરવામાં આવે છે ત્યારે વધેલા ભાગની જડત્વની ચાક્માત્રા તે જ અક્ષને અનુલક્ષીને $\frac{ NI _{0}}{16}$ હોય તો $N=......$View Solution
- 3એક પાતળી ચોરસ તકતી જેનું દળ $m$ અને બાજુની લંબાઈ $a$ છે તેના વિકર્ણને અનુલક્ષીને જડત્વની ચાકમાત્રા $I$ હોય તો ...View Solution
- 4View Solutionપોલો અને ઘન ગોળાના દળ અને જડત્વની ચાકમાત્રા સમાન હોય,તો ત્રિજયાનો ગુણોત્તર કેટલો થાય?
- 5સળિયાના કેન્દ્રમાંથી પસાર થતી અને લંબાઇને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I_1$ છે.તેમાંથી રીંગ બનાવતા કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I_2$ છે.તોView Solution
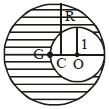
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $\mathrm{R}$ ત્રિજ્યાના ગોળામાથી $1$ ત્રિજ્યાનો ગોળો કાપી નાખવામાં આવેલ છે વધેલા ભાગનું દ્રવ્યમાનકેન્દ્ર $G$ આગળ મળતું હોય તો $R$ કયા સમીકરણ વડે મેળવી શકાય?View Solution
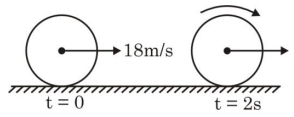
- 7$0.5\,kg$ દળ અને $r$ ત્રિજ્યાવાળી નિયમિત આકારની તકતીને $t =0\,s$ સમયે $18\,m / s$ જેટલા વેગથી ખરબચડી સમક્ષિતિજ સપાટી પર પ્રક્ષિપ્ત કરવામાં આવે છે. $t=0\,s$ સમયે તે શુદ્ધ સરકતી ગતિની શરૂઆત કરે છે. $t=2\,s$ બાદ તે શુદ્ધ લોટણ ગતિ પ્રાપ્ત કરે છે. (આકૃતિમાં જુઓ). તકતીની $2\,s$ બાદ કુલ ગતિ ઉર્જા $..........J$ થાય.(ધર્ષણાંકનું મૂલ્ય $0.3$ અને $g=10\,m / s ^2$ આપેલ છે.)View Solution
- 8એક કણ $a$ ત્રિજયાના વર્તુળ પર અચળ ઝડપથી ગતિ કરે છે.$AB$ વ્યાસ અને $C$ કેન્દ્ર છે.તો કણ $B$ પર હોય,ત્યારે $A$ અને $C$ ને અનુલક્ષીને કોણીય ઝડપનો ગુણોત્તર કેટલો થાય?View Solution
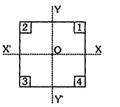
- 9આકૃતિમાં નિયમિત ચોરસ પ્લેટ દર્શાવેલી છે. જેના ખૂણા પરથી ચાર સમાન ચોરસ દૂર કરવામાં આવ્યા છે.ચોરસ $-1$ ને દૂર કરતાં $ C.M.$ ક્યાં મળશે ?View Solution
- 10એક $\theta $ કોણવાળા ઢાળ પરથી સરકયા સિવાય ગબડીને અને ગબડયા સિવાય સરકીને નીચે આવતાં ઘન ગોળા (દળ $m$ અને ત્રિજયા $ R$) ના પ્રવેગનો ગુણોત્તર કેટલો થાય?View Solution
