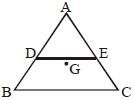
Let side of triangle is a and mass is \(m\)
\(MOI\) of plate \(ABC\) about centroid
\(I_{0}=\frac{m}{3}\left(\left(\frac{a}{2 \sqrt{3}}\right)^{2} \times 3\right)=\frac{m a^{2}}{12}\)
triangle \(ADE\) is also an equilateral triangle of side \(a / 2\)
Let moment of inertia of triangular plate \(ADE\) about it's centroid \((G')\) is \(I _{1}\) and \(mass\) is \(m _{1}\)
\(m _{1}=\frac{ m }{\frac{\sqrt{3} a ^{2}}{4}} \times \frac{\sqrt{3}}{4}\left(\frac{ a }{2}\right)^{2}=\frac{ m }{4}\)
\(I _{1}=\frac{ m _{1}}{12}\left(\frac{ a }{2}\right)^{2}=\frac{ m }{4 \times 12} \frac{ a ^{2}}{4}=\frac{ ma ^{2}}{192}\)
distance \(G G^{\prime}=\frac{a}{\sqrt{3}}-\frac{a}{2 \sqrt{3}}=\frac{a}{2 \sqrt{3}}\)
so \(MOI\) of part \(ADE\) about centroid \(G\) is
\(I _{2}= I _{1}+ m _{1}\left(\frac{ a }{2 \sqrt{3}}\right)^{2}=\frac{ ma ^{2}}{192}+\frac{ m }{4} \cdot \frac{ a ^{2}}{12}\)
\(=\frac{5 ma ^{2}}{192}\)
now \(MOI\) of remaining part
\(=\frac{m a^{2}}{12}-\frac{5 m a^{2}}{192}=\frac{11 m a^{2}}{12 \times 16}=\frac{11 I_{0}}{16}\)
\(\Rightarrow \quad N=11\)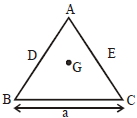
Download our appand get started for free
Similar Questions
- 1પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_1$ જડત્વની ચાકમાત્રા ધરાવતી તકતી આ અક્ષને અનુલક્ષીને $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. હવે, પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_2$ જેટલી જડત્વની ચાકમાત્રા ધરાવતી બીજી તકતી આ તકતી પર મૂકવામાં આવે, તો આ બંને તકતીનો સંયુક્ત કોણીય વેગ કેટલો હશે ?View Solution
- 2સમાન દ્રવ્ય અને જાડાઇ ધરાવતી તકતીની ત્રિજયા $ 0.2\,m$ અને $0.6\,m $ છે.તો તેની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રાનો ગુણોત્તર કેટલો થાય?View Solution
- 3બે તકતીની પોતાના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે ${I}_{1}$ અને ${I}_{2}$ છે. તેમની કોણીય ઝડપ અનુક્રમે $\omega_{1}$ અને $\omega_{2}$ છે અને તેમની એક્ષાને એક કરી દેવામાં આવે તો આ પ્રક્રિયામાં તંત્રની ગતિઊર્જામાં થતો ઘટાડો કેટલો હશે?View Solution
- 4$m$ દળ અને $r$ ત્રિજયાની એક નિયમિત વર્તુળાકાર રીંગ તેના સમતલને લંબ અને તેના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $\omega$ કોણીય ઝડપથી ભ્રમણ કરે છે. તેની ગતિઊર્જા કેટલી થાય?View Solution
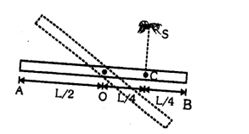
- 5આકૃતિમાં નિયમિત સળિયો $AB $ની લંબાઇ $ L$ અને દળ $M$ છે તેને તેના કેન્દ્ર $ O$ પર એવી રીતે કિલકીત કરેલો છે જેથી શિરોલંબ સમતલમાં મુક્તપણે ભ્રમણ કરી શકે છે. સળિયો પ્રારંભમાં સમક્ષિતિજ સ્થિતિમાં છે તેટલાજ દળ $M $ નું પદાર્થ $S$ શિરોલંબમાંથી $v$ વેગથી $C$ બિંદુ પર પડે છે. $C$ એ $ O$ અને $B$ વચ્ચેનું મધ્યબિંદુ છે. પદાર્થના પતનની તરત જ બાદ સળિયાનો કોણીય વેગ શોધો.View Solution
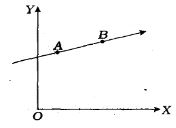
- 6$m$ દળનો એક કણ $XY$ સમતલમાં $AB$ સીધા માર્ગે $v$ વેગથી ગતિ કરે છે. સંદર્ભબિંદુ $O$ ને અનુલક્ષીને $A$ બિંદુએ કણનું કોણીય વેગમાન $L_A $ અને $B$ બિંદુએ $L_B$ હોય, તો ........View Solution
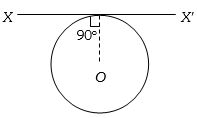
- 7$L$ લંબાઇ અને $\rho $ રેખીય ઘનતા ધરાવતા તારને વર્તુળમાં વાળતાં $XX'$ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 8જો $\overrightarrow{ F }=3 \hat{i}+4 \hat{j}-2 \hat{k}$ બળ એ $2 \hat{i}+\hat{j}+2 \hat{k}$ સ્થાન સદીશ ધરાવતા કણ ઉપર લાગતો હોય, તો ઊગમબિંદુને અનુલક્ષીને ટોર્ક............હશેView Solution
- 9$70\, kg$ નો એક માણસ બેઠેલી સ્થિતિમાથી હવામાં ઊભી છલાંગ લગાવે છે. કૂદકો મારીને પોતાને ઊંચકવા માટે તે માટે માણસ જમીનને અચળ બળ $F$ થી ધકેલે છે. તે કૂદકો મારે તે પહેલા દ્રવ્યમાન કેન્દ્ર $0.5\, m$ જેટલું ઊંચકાય છે. કૂદકો માર્યા પછી દ્રવ્યમાન કેન્દ્ર વધુ $1\, m$ ઉપર જાય છે. તો સ્નાયુઓ દ્વારા આપવામાં આવેલ પાવર કેટલો હશે? ( $g\, = 10\, ms^{-2}$)View Solution
- 10$2\ m$ ત્રિજ્યાની વર્તૂળાકાર તકતી $ 240 $ ભ્રમણ/મિનિટ થી ભ્રમણ કરે છે તકતીને ટોર્ક આપતા તે $\pi\ radian/s^2$ ના દરથી ધીમી પડે છે તો કેટલા સમયમાં તે અટકશે. સ્થિર થતા પહેલા તકતી કેટલા ભ્રમણ પૂર્ણ કરશે?View Solution
