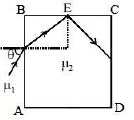
$30 \,cm$ કેન્દ્રલંબાઈ ધરાવતા એક બહિર્ગોળ લેન્સથી $60\, cm$ અંતરે એક બિંદુવત વસ્તુ રાખવામાં આવેલ છે. જે એક સમતલ અરીસાને લેન્સની મુખ્ય અક્ષને લંબરૂપે અને તેનાથી $40\, cm$ અંતરે મૂકવામાં આવતા, અંતિમ પ્રતિબિંબ $....$ અંતરે રચાશે.

NEET 2021, Diffcult
d
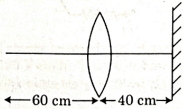
First for image formation from lens
First for image formation from lens
\(\mathrm{u}=-60\, \mathrm{~cm}\)
\(\mathrm{f}=+30\, \mathrm{~cm}\)
\(\Rightarrow \mathrm{v}=\frac{\mathrm{uf}}{\mathrm{u}+\mathrm{f}}=\frac{-60 \times 30}{-60+30}=60\, \mathrm{~cm}\)
This real image formed by lens acts as virtual object for mirror
Real image from plane mirror is formed \(20 \mathrm{~cm}\) in front of mirror, hence at \(20 \mathrm{~cm}\) distance from lens. Now for second refraction from lens,
\(\mathrm{u}=-20\, \mathrm{~cm}\)
\(\mathrm{f}=+30\, \mathrm{~cm}\)
\(v=\frac{\mathrm{uf}}{\mathrm{u}+\mathrm{f}}=\frac{-20 \times 30}{-20+30}=-60\, \mathrm{~cm}\)
So, final virtual image is \(60\, \mathrm{~cm}\) from lens, or \(20\, \mathrm{~cm}\) behind mirror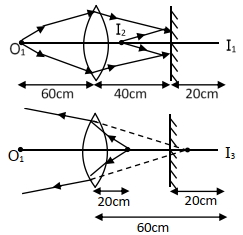
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionજો તરંગ ધટ્ટ માધ્યમમાં વક્રીભવન અનુભવે તો નીચેનામાંથી કયું સાયું છે?
- 2$f$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાના ધ્રુવ પાસે સૂર્ય (વ્યાસ $d$) $\theta$ રેડિયન ખૂણો આંતરે છે. તો અરીસાની વડે રચાતા સૂર્યના પ્રતિબિંબનો વ્યાસ..... હશે.View Solution
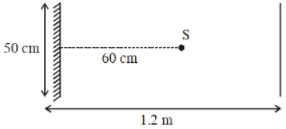
- 3પ્રકાશનો બિંદુવત ઉદગમ $S, 50\, cm$ પહોંળાઈ ધરાવતા દિવાલ પર શિરોલંબ લટકાવેલ સાદા અરીસાના કેન્દ્રની સામે $60\, cm$ ના અંતરે ગોઠવાયેલો છે. આકૃતિમાં દર્શાવ્યા મુજબ એક માણસ આ અરિસાથી $1.2\, m$ દૂરના અંતરે, અરીસાને સમાંતર લીટી પર ચાલે છે. અરીસામાં દષ્યમાન પ્રકાશનું પ્રતીબિંબ, ચરમ બિંદુઓ (extreme points) થી .......$cm$ અંતરે આવેલ છે.View Solution
- 4ન્યૂનત્તમ વિચલન કોણ એ સમબાજુ પ્રિઝમના પ્રિઝમકોણ જેટલો છે. કયા.......$^o$ આપાત કોણે ન્યૂનત્તમ વિચલન મળશે?View Solution
- 5$1.54$ વક્રીભવનાંક વાળા કાચમાંથી બનાવેલ $6^{\circ}$ કોણ ધરાવતા પાતળા પ્રિઝમ $P_1$ ને $1.72$ વક્રીભવનાંકવાળા કાચમાંથી બનાવેલ બીજા પ્રિઝમ $P_2$ સાથે જોડવામાં આવે છે કે જેથી સરેરાશ વિચલન સિવાય વિભાજન થાય. કોણ $P_2$ નો કોણ $.............{}^{\circ}$ હશે.View Solution
- 6$f $ કેન્દ્રલંબાઇ ધરાવતા બહિર્ગોળ અરીસાના ધ્રુવથી $f$ અંતરે વસ્તુ મૂકતાં પ્રતિબિંબ કયાં મળશે?View Solution
- 7$5^o $ નો પ્રિઝમકોણ ધરાવતા પ્રિઝમ પર સફેદ પ્રકાશ આપાત કરવામાં આવે છે.લાલ અને વાદળી રંગના વક્રીભવનાંક $1.64$ અને $1.66$ હોય,તો બંને રંગ વચ્ચેનો વિચલનકોણ કેટલા ......$^o$ થશે?View Solution
- 8પ્રિઝમનો વક્રીભવનાંક $\sqrt 2 $ અને પ્રિઝમકોણ $60^o $ હોય,તો લઘુત્તમ વિચલન માટે આપાતકોણ કેટલા .....$^o$ હોવો જોઈએ?View Solution
- 9સંયુક્ત માઇક્રોસ્કોપના વસ્તુકાંચ અને નેત્રકાંચની કેન્દ્રલંબાઈ અનુક્રમે $1.2\, cm$ અને $3.0\, cm$ છે. જો વસ્તુને વસ્તુકાંચથી $1.25\, cm$ અંતરે મૂકવામાં આવે તો અંતિમ પ્રતિબિંબ અનંત અંતરે મળે છે. તો આ સંયુક્ત માઇક્રોસ્કોપની મોટવણી કેટલી હશે?View Solution
- 10$d$ બાજુ અને $\mu_2$ વક્રીભવનાંક ધરાવતા પારદર્શક ઘનને $\mu_1(\mu_1 < \mu_2)$ વક્રીભવનાંક ધરાવતા પ્રવાહીમાં મુકેલ છે આકૃતિમાં દર્શાવ્યા પ્રમાણે $AB$ બાજુ પરથી એક પ્રકાશનું કિરણ $\theta $ ખૂણે આપત કરવામાં આવે છે જે $BC$ બાજુ પર $E$ બિંદુ આગળ પૂર્ણ આંતરિક પરાવર્તન પામે છે. આ માટે $\theta $ નું મૂલ્ય કેટલું હોવું જોઈએ?View Solution