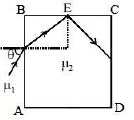
$d$ બાજુ અને $\mu_2$ વક્રીભવનાંક ધરાવતા પારદર્શક ઘનને $\mu_1(\mu_1 < \mu_2)$ વક્રીભવનાંક ધરાવતા પ્રવાહીમાં મુકેલ છે આકૃતિમાં દર્શાવ્યા પ્રમાણે $AB$ બાજુ પરથી એક પ્રકાશનું કિરણ $\theta $ ખૂણે આપત કરવામાં આવે છે જે $BC$ બાજુ પર $E$ બિંદુ આગળ પૂર્ણ આંતરિક પરાવર્તન પામે છે. આ માટે $\theta $ નું મૂલ્ય કેટલું હોવું જોઈએ?
JEE MAIN 2019, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન કેન્દ્રલંબાઈ $(f)$ના પાતળા લેન્સ,પણ એક બહિર્ગોળ અને બીજો અંતર્ગોળ એક્બીજાના સંપર્કમાં રાખેલ છે. આ સંયોજનની સમતુલ્ય કેન્દ્રલંબાઈ $.......$ થાય.View Solution
- 2બર્હિગોળ લેન્સ માટે કેન્દ્રલંબાઇ શોધવાના પ્રયોગમાં વસ્તુ $u$ અને પ્રતિબિંબ અંતર $v$ નો આલેખ કેવો થાય?View Solution
- 3$2d \,cm$ ઊંડાઇ ધરાવતી ટાંકીમાં ${\mu _1}$ વક્રીભવનાંક ધરાવતું પ્રવાહી અડધી ઊંચાઇ અને ${\mu _2}$ વક્રીભવનાંક ધરાવતું પ્રવાહી અડધી ઊંચાઇ સુધી ભરેલ છે.તો તળિયું કેટલી ઊંડાઇ પર દેખાય?View Solution
- 4View Solutionઅંતર્ગોળ અરીસા માટે વાસ્તવિક પ્રતિબિંબ પદાર્થ અને પ્રતિબિંબ વચ્ચેનું ન્યૂનત્તમ અંતર ...........છે.
- 5ઘટ્ટ માધ્યમનો પાતળા માધ્યમની સાપેક્ષે વક્રીભવનાંક $n_{12}$ અને તેનો ક્રાંતિકકોણ $\theta_C$ છે. જ્યારે પ્રકાશ ઘટ્ટ માધ્યમમાંથી પાતળા માધ્યમમાં ગતિ કરતો હોય ત્યારે તે સપાટી પાસે $A$ ખૂણે આપત થાય છે, જેમાંથી થોડોક ભાગ પરાવર્તન પામે છે અને બીજો ભાગ વક્રીભવન પામે છે. પરાવર્તિતકિરણ અને વક્રીભૂતકિરણ વચ્ચેનો ખૂણો $90^o$ હોય તો આપતકોણ $A$ કેટલો હશે?View Solution
- 6$+ 2.50 D$ અને $-3.75 D$ ડાયોપ્ટરના લેન્સને સંપર્કમાં રાખતાં તંત્રની કેન્દ્રલંબાઇ કેટલા ....$cm$ થાય?View Solution
- 7એક વ્યક્તિ $-1.0$ ડાયપ્ટર પાવર ધરાવતા ચશ્માનો દૂરની વસ્તુ જોવા માટે અને $2.0$ ડાયપ્ટર પાવર ધરાવતા વાંચવાના કાચનો ઉપયોગ કરે છે. વ્યક્તિ માટે લઘુતમ દ્રષ્ટિ અંતર $..........\,cm$ હશે.View Solution
- 8તેજસ્વી પ્રકાશ ઉદગમથી $10\ cm$ દુર રાખેલ બહિર્ગોળ લેન્સ તેનાથી $10\ cm$ દુર રાખેલ પડદા પર તીવ્ર (સ્પષ્ટ) પ્રતિબિંબ બનાવે છે. $1.5\ cm$ જાડાઇવાળા એક કાચના ચોસલા (જેનો વક્રીભવનાંક $1.5$ છે)ને પ્રકાશ ઉદગમની ઊપર મુકવવામાં આવે છે. ફરી તીવ્ર (સ્પષ્ટ) પ્રતિબિંબ મેળવવા માટે પડદાને $d$ અંતરે ખસેડવામાં આવે છે. તો $d$ કેટલો હશે?View Solution
- 9ગેલિલીયન ટેલિસ્કોપના વસ્તુકાંચ અને નેત્રકાંચની કેન્દ્રલંબાઈ અનુક્રમે $30\, cm$ અને $3.0\, cm$ છે. ટેલિસ્કોપથી દૂર પડેલી વસ્તુનું આભાસી અને મોટું પ્રતિબિંબ નેત્રકાંચથી નજીકતમ બિંદુ આગળ મળે છે. તો આ કિસ્સામાં ટેલિસ્કોપની મોટવણી કેટલી મળશે?View Solution
- 10ધારો કે બે પારદર્શક માધ્યમોને $x - z$ સમતલથી અલગ કરવામાં આવ્યા છે. $Z \geq 0$ માટે માધ્યમ $1$ નો વક્રીભવનાંક $\sqrt{2}$ અને $z <0$ માટ માધ્યમ $2$ નો વક્રીભવનાંક $\sqrt{3}$ છે. પ્રકાશનું કિરણ આ સમતલ પર આપાત થાય છે. જેનું સમીકરણ $\vec{ A }=6 \sqrt{3} \hat{ i }+8 \sqrt{3} \hat{ j }-10 \hat{ k }$ છે. માધ્યમ $-2$ માં આ કિરણ કેટલાના ખૂણે વક્રીભૂત થશે?View Solution