લેન્સની સામે વસ્તુ હોવાથી તે વાસ્તવિક છે અને \(h_1 = 25\,\, cm, f = 30 cm, h_2 = -50 \,\,cm\)
\(m\,\, = \,\,\,\frac{{{h_2}}}{{{h_1}}}\,\, = \,\,\frac{{ - 50}}{{25}}\,\, = \,\, - 2\)
\(m\,\, = \,\,\,\frac{{f}}{{{f} + u}}\,\,\, \Rightarrow \,\,\, - 2\,\, = \,\,\,\frac{{30}}{{30 + u}}\)
\(u\,\, = \,\, - 45\,\,cm\,\,\,\,\, \Rightarrow \,\,m\,\, = \,\,\frac{v}{u}\,\,\,\,\, \Rightarrow \,\, - 2\,\, = \,\,\frac{v}{{ - 45}}\,\,\,\, \Rightarrow \,\,\,v\,\, = \,\,90\,\,cm\)
આ પરિસ્થિતી જેમ, (જેવી રીતે) વસ્તુ અને પ્રતિબિંબ લેન્સની વિરુદ્ધ બાજુએ (દિશાએ) હોય છે.તો વસ્તુ અને પ્રતિબિંબ વચ્ચેનું અંતર \(1 = u + v = 45 + 90 = 135\,\, cm\)
જો પ્રતિબિંબ સીધું હોય (તેથી, આભાસી)
\(m\,\, = \,\,\frac{{f}}{{{f} + u}}\,\,\,\, \Rightarrow \,\,2\,\, = \,\,\frac{{30}}{{30 + u}}\,\,\,\, \Rightarrow \,\,\,u\,\, = \,\, - 15\,\,cm\,\,\,\,\)
\( \Rightarrow \,\,m\,\, = \, - \,\,\frac{v}{u}\,\,\,\,\, \Rightarrow \,\,2\,\, = \,\,\frac{{ - v}}{{ - 15}}\,\,\,\,\, \Rightarrow \,\,\,\,v\,\, = \,\,\,30\,\,cm.\)
આ પરિસ્થિતી કાચ અને પ્રતિબિંબ બને લેન્સની સામે હોવાથી વસ્તુ અને પ્રતિબિંબ વચ્ચેનું અંતર \(2 = v - u = 30 - 15 = 15\,\, cm\) 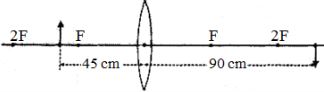
Download our appand get started for free
Similar Questions
- 1સંયુક્ત માઇક્રોસ્કોપના વસ્તુકાંચ અને નેત્રકાંચની કેન્દ્રલંબાઈ અનુક્રમે $1.2\, cm$ અને $3.0\, cm$ છે. જો વસ્તુને વસ્તુકાંચથી $1.25\, cm$ અંતરે મૂકવામાં આવે તો અંતિમ પ્રતિબિંબ અનંત અંતરે મળે છે. તો આ સંયુક્ત માઇક્રોસ્કોપની મોટવણી કેટલી હશે?View Solution
- 2$20$ $cm$ ના મૂલ્યની કેન્દ્રલંબાઇ ધરાવતા એક અભિસારી કાચથી $15$ $cm$ દૂર જેની કેન્દ્રલંબાઇનું મૂલ્ય $25$ $cm$ છે.તેવો એક અપસારી કાચ મૂકેલ છે,એક સમાંતર પ્રકાશપૂંજ આ અપસારી કાચ પર પડે છે.આમ રચાતું અંતિમ પ્રતિબિંબ થશે.View Solution
- 3View Solutionહાયપર-મેટ્રોપિયા શું છે?
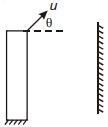
- 4એક દડાને ટેબલની ટોચ પરથી $\theta$ ખૂણે પ્રારંભિક ઝડપ $u$ સાથે પ્રક્ષેપિત કરવામાં આવ્યો છે, દડાની સાપેક્ષમાં પ્રતિબિંબની ગતિ કવી છે ?View Solution
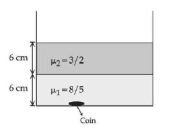
- 5મિશ્રિત ન થઈ શકે તેવા અનુકમે $\frac{8}{5}$ અને $\frac{3}{2}$ વકીભવનાંક ધરાવતા બે પ્રવાહીને આક્રૂતિમાં દર્શાવ્યા મુજબ રાખવામાં આવેલ છે. પ્રત્યેક પ્રવાહી સ્થંભની ઉંચાઈ $6 \mathrm{~cm}$ છે. બીકરના તળિયે એક સિક્કો મૂકેલો છે. નજીકતમ દષ્ટિ અંતર માટે, સિક્કાની આભાસી ઉંડાઈ $\frac{\alpha}{4} \mathrm{~cm}$ છે. $\alpha$ નું મૂલ્ય_______છે.View Solution
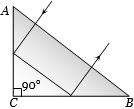
- 6View Solutionઆપેલ સમદ્વિબાજુ પ્રિઝમના વક્રીભવનાંકનું લઘુત્તમ મૂલ્ય કેટલું હોવું જોઈએ?
- 7ઘટ્ટ માધ્યમનો પાતળા માધ્યમની સાપેક્ષે વક્રીભવનાંક $n_{12}$ અને તેનો ક્રાંતિકકોણ $\theta_C$ છે. જ્યારે પ્રકાશ ઘટ્ટ માધ્યમમાંથી પાતળા માધ્યમમાં ગતિ કરતો હોય ત્યારે તે સપાટી પાસે $A$ ખૂણે આપત થાય છે, જેમાંથી થોડોક ભાગ પરાવર્તન પામે છે અને બીજો ભાગ વક્રીભવન પામે છે. પરાવર્તિતકિરણ અને વક્રીભૂતકિરણ વચ્ચેનો ખૂણો $90^o$ હોય તો આપતકોણ $A$ કેટલો હશે?View Solution
- 8જ્યારે ક્રાઉન અને ફ્લીન્ટ ગ્લાસને અવર્ણક (achromatic) રીતે સંયોજીત કરી બનાવેલા પ્રિઝમમાં પીળા-કિરણ માટે $2^{\circ}$ જેટલું વિચલન મળે છે. ક્રાઉન અને ફ્લીન્ટ ગ્લાસ માટે ડીસ્પર્સીવ (dispersive) પાવર અનુક્રમે $0.02$ અને $0.03,$ અને પીળા પ્રકાશ માટે આ ગ્લાસો માટે વક્રીભવનાંક અનુક્રમે $1.5$ અને $1.6$ લો. ક્રાઉન ગ્લાસ માટે વક્રીભવન કોણ $........\,^{\circ}$ હશે. (નજીકત્તમ પૂર્ણાકમાં લખો)View Solution
- 9આકૃતિમાં દર્શાવ્યા મુજબ એક કાચ ($\mu = 1.5)$ અંદર એક હવાનો પરપોટો $10\, cm$ વ્યાસ ધરાવતી ગોળાકાર સપાટીથી $3 \, cm $ અંતરે રહેલો છે. જો સપાટી બહિર્ગોળ હોય તો સપાટી પરથી ......$cm$ અંતરે પરપોટો દેખાશે.View Solution
- 10$\sqrt{3}$ જેટલો વક્રીભવનાંક ધરાવતા કાચના ચોસલા ઉપર પ્રકાશ કિરણ $60°$ ના કોણે આપાત કરાવવામાં આવે છે. વક્રીભવન પામ્યા બાદ પ્રકાશ કિરણ બીજી સમાંતર સપાટીમાંથી નિર્ગમન પામે છે અને આપાત કિરણ અને નિર્ગમન કિરણ વચ્ચે લેટરલ શિફટ $4 \sqrt{3} cm$ જેટલું મળે છે. કાચના ટૂકડાની જાડાઈ...... $cm$ હશે.View Solution
