$30\,cm$ બાજુ ધરાવતું ઘન ચોસલું લીસ્સી સમક્ષિતિજ સપાટી પર $2\,\,ms^{-1}$ વેગથી ગતિ કરે છે. આકૃતિમાં બતાવ્યા મુજબ સપાટીમાં બિંદુ $O$ પર ટેકરો છે. તો ટેકરા સાથે અથડામણ બાદ તરત જ ચોસલાનો કોણીય વેગ કેટલો હશે?
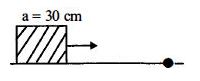

JEE MAIN 2016, Diffcult
b
Angular momentum, \(mvr = I\omega \)
Angular momentum, \(mvr = I\omega \)
momrnt of Inertia \((I)\) of cubical block is given by
\(\begin{array}{l}
I = m\left( {\frac{{{R^2}}}{6} + {{\left( {\frac{R}{{\sqrt 2 }}} \right)}^2}} \right)\\
\therefore \,\,\omega = \frac{{m.2\frac{R}{2}}}{{m\left( {\frac{{{R^2}}}{6} + {{\left( {\frac{R}{{\sqrt 2 }}} \right)}^2}} \right)}}\\
\Rightarrow \omega = \frac{{12}}{{8R}} = \frac{3}{{2 \times 0.3}} = \frac{{10}}{2} = 5\,rad/s.
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$20 \,Nms$ નો કોણીય આઘાત $2\, kg$ દળ અને $20 \,cm$ ત્રિજ્યા ધરાવતા પોલા નળાકાર પર લગાડવામાં આાવે છે. તેની કોણીય ઝડપમાં થતો ફેરફાર .......... $rad / s$ થાય.View Solution
- 2એક તકતી $\omega$ કોણીય ઝડપથી ભ્રમણ કરે છે. જો એક બાળક તેના પર બેસેલું હોય, તો નીચેનામાથી શેનું સંરક્ષણ થાય?View Solution
- 3એક દડો સરકયા વિના ગબડે છે.દડાના દ્રવ્યમાન કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજયા $K$ છે.જો દડાની ત્રિજયા $R$ હોય, તો કુલઊર્જાનો કેટલામો ભાગ ચાકગતિ ઊર્જાના સ્વરૂપમાં હશે?View Solution
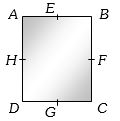
- 4એક લંબચોરસ $ABCD \,(BC=2AB)$ માં ન્યૂનતમ જડત્વની ચાકમાત્રા કઈ અક્ષને અનુલક્ષીને હોય?View Solution
- 5$M$ દળ અને $L$ લંબાઇ ધરાવતા નિયમિત સળિયાના મધ્યબિંદુમાંથી પસાર થતી અને લંબાઇને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I_0$ છે. છેડામાંથી પસાર થતી અને લંબાઇને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 6View Solutionઢોળાવવાળા સમતલ પર તકતી સરક્યા વિના ગબડે છે. તો તેની કુલ ઊર્જાનો કેટલામો ભાગ ચાકગતિ ઊર્જા સ્વરૂપે મળશે ?
- 7બે તકતીની પોતાના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે ${I}_{1}$ અને ${I}_{2}$ છે. તેમની કોણીય ઝડપ અનુક્રમે $\omega_{1}$ અને $\omega_{2}$ છે અને તેમની એક્ષાને એક કરી દેવામાં આવે તો આ પ્રક્રિયામાં તંત્રની ગતિઊર્જામાં થતો ઘટાડો કેટલો હશે?View Solution
- 8$100\,kg$ દળનો માણસ એ $200\,kg$ ના પ્લેટફોર્મ પર ઉભો છે. જે સૂવાળી બરફની સપાટી પર છે. જો માણસ પ્લેટફોર્મ પર $30\,m / s$ ના વેગથી ગતિ કરે છે, તો $..........m/s$ વેગથી પ્લેટફોર્મ એ બરફની સાપેક્ષમાં પાછુ ખસશે.View Solution
- 9$1\ m$ લંબાઈના હલકાં સળિયાના છેડે $ 5\ kg $ દળના બે ગોળા $ A$ અને $B $ જોડેલા છે. આ દળને બિંદુવત ધારો $A $ માંથી પસાર થતી અને મધ્યબિંદુમાંથી પસાર થતી સળિયાની લંબાઈને લંબ અક્ષો પર જડત્વની ચાકમાત્રાનો ગુણોત્તર ...... થશે.View Solution
- 10View Solutionતંત્રનું દ્રવ્યમાનકેન્દ્ર શેના પર આધાર રાખતું નથી?
