$M$ દળ અને $L$ લંબાઇ ધરાવતા નિયમિત સળિયાના મધ્યબિંદુમાંથી પસાર થતી અને લંબાઇને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I_0$ છે. છેડામાંથી પસાર થતી અને લંબાઇને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?
AIPMT 2011, Medium
b
According to the theorem of parallel axes, the moment of inertia of the thin rod of mass \(M\) and length \(L\) about an axin passing through one of the ends is
According to the theorem of parallel axes, the moment of inertia of the thin rod of mass \(M\) and length \(L\) about an axin passing through one of the ends is
\(I = {I_{CM}} + M{d^2}\)
Where \({I_{CM}}\) is the moment of inertia of the given rod about an axis passing through its center of mass and perpendicular to its lenght and \(d\) is the distance between two parallel axes.
Herer, \({I_{CM}} = {I_{0'}}\,d = \frac{L}{2}\)
\(\therefore \,I = {I_0} + M{\left( {\frac{L}{2}} \right)^2} = {I_0} + \frac{{M{L^2}}}{4}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$200\, kg$ના પ્લેટફોર્મના પરિઘ પર $80\, kg$ નો માણસ હોય ત્યારે તેની અક્ષને અનુલક્ષીને કોણીય ઝડપ $5\;rpm$ છે. હવે માણસ ચાલીને કેન્દ્ર પર જાય ત્યારે તે પ્લેટફોર્મની કોણીય ઝડપ ....... $rpm$View Solution
- 2એક $\theta $ કોણવાળા ઢાળ પરથી સરકયા સિવાય ગબડીને અને ગબડયા સિવાય સરકીને નીચે આવતાં ઘન ગોળા (દળ $m$ અને ત્રિજયા $ R$) ના પ્રવેગનો ગુણોત્તર કેટલો થાય?View Solution
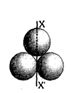
- 3$M$ દળ અને $R $ ત્રિજ્યાના ત્રણ ધન ગોળાઓ આકૃતિમાં દર્શાવ્યા પ્રમાણે છે. તંત્રની અક્ષ $XX'$ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 4View Solutionએક નિશ્ચિત બિંદુની આસપાસ સમતલમાં કોઈ દળ ભ્રમણ કરે છે, તેનું કોણીય વેગમાન કઈ દિશામાં હશે?
- 5View Solutionકણ નિયમિત વર્તુળમય ગતિ કરે છે. કયાં બિંદુની સાપેક્ષે તેનું કોણીય વેગમાન અચળ રહે છે.
- 6$f_0 = 1.3\, rev/sec$ આવૃતિથી ભ્રમણ કરતી વર્તુળાકાર તકતી $30\, seconds$ માં સ્થિર થાય છે. તો અંદાજિત કોણીય પ્રવેગ ....... $rad/{\sec ^2}$ થશે.View Solution
- 7$10\ kg $ દળ અને $ 50\ m $ ની ચક્રાવર્તનની ત્રિજ્યા ધરાવતી તકતી પર $10^5\ [N - m]$ નું બળ યુગ્મ લગાડવામાં આવે છે. કોણીય પ્રવેગની કિંમત $rad/sec^2$ માં કેટલી થશે ?View Solution
- 8$M$ દળ ધરાવતો પદાર્થ $A$ ગુરુત્વાકર્ષણ બળની અસર હેઠળ પડતાં તે બે ટુકડાઓમાં વિભાજિત થાય છે. એક ટુકડો $B$ નું દળ $1/3\ M$ અને બીજા ટુકડા $ C$ નું દળ $ 2/3\ M$ છે. પદાર્થ $A$ ના દ્રવ્યમાન કેન્દ્રની સાપેક્ષે ટુકડાઓ $ B$ અને $ C$ થી બનતાં તંત્રનું દ્રવ્યમાન-કેન્દ્ર .....View Solution
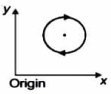
- 9View Solutionએક કણ વર્તુળમાં નિયમિત ઝડપે નીચે દર્શાવ્યા પ્રમાણે પરિભ્રમણ કરી રહ્યોં છે. ઉગમબિંદુના સંદર્ભમાં કણનું કોણીય વેગમાન શું થાય?
- 10એક વર્તુળાકાર તકતી $L$ લંબાઈના ઢાળ પરથી ઉપરથી નીચે આવે છે, જ્યારે તે ઢાળ પર સરકીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{1}$ છે. જ્યારે તે ગબડીને નીચે આવે ત્યારે તેને લાગતો સમય $t_{2}$ છે. તો $\frac{t_{2}}{t_{1}}$ નું મૂલ્ય $\sqrt{\frac{3}{x}}$ છે, તો $x$ નું મૂલ્ય કેટલું હશે?View Solution
