$30^o $ ના ખૂણાવાળા ઢાળ પર પોલો નળાકાર મૂકતાં $10\ m$ અંતર કાપ્યા પછી તેનો વેગ.......... $m/s$
Medium
c
The distance of \(10\) \(\mathrm{m}\) on the hypotenuse on an incline of \(30^{\circ}\) corresponds to a height difference of \(5.\) Thus change in potential energy is given as \(5mg.\)
The distance of \(10\) \(\mathrm{m}\) on the hypotenuse on an incline of \(30^{\circ}\) corresponds to a height difference of \(5.\) Thus change in potential energy is given as \(5mg.\)
The change in the kinetic energy is given as
\(\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}\)
moment of inertia of a hollow cylinder about centroidal axis is \(m r^{2}\)
Thus we get the kinetic energy as
\(\frac{1}{2} m v^{2}+\frac{1}{2} m r^{2} \frac{v^{2}}{r^{2}}\)
or
\(m v^{2}\)
Equating both the energies we get
\(5 m g=m v^{2}\)
or
or \(v=\sqrt{49}=7 m / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસુરેખ સપાટી પર કોઈ તકતી સરક્યાં વગર ગબડે છે. તો રેખીય ગતિઉર્જા નો કુલ ગતિઉર્જા સાથેનો ગુણોત્તર શું મળે?
- 2$30^o $ ના ખૂણા ધરાવતા ઢાળ પરથી નકકર ગોળો ગબડે ત્યારે,તેનો પ્રવેગView Solution
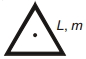
- 3$m$ દળ અને $L$ લંબાઈવાળા ત્રણ સળિયાઓને એક સમભુજ ત્રિકોણ બનાવવા માટે નીચે આકૃતિમાં બતાવ્યા અનુસાર જોડવામાં આવે છે. તેના સમતલને લંબ અને તંત્રના દ્રવ્યમાન કેન્દ્ર માંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા શું થાય?View Solution
- 4$5 \hat{i}+3 \hat{j}-7 \hat{k}$ બળ દ્વારા ઉગમબિંદુને ફરતે લાગતુ ટોર્ક $\tau$ છે.જો આ બળ કે જેનો સ્થાન સદિશ $2 \hat{i}+2 \hat{j}+\hat{k}$ હોય પર લાગે તો ટોર્ક $\tau$ નું મૂલ્ય $........$ હશે.View Solution
- 5જો $5\, sec$ માં થતો કોણીય વેગમાનનો ફેરફાર $1\,J$ થી $5\, J$ છે. તો ટોર્ક કેટલો હશે?View Solution
- 6View Solutionઘન ગોળા માટે ચાકગતિ અને રેખીયગતિ ઊર્જા નો ગુણોત્તર
- 7એક એન્જિનની મોટર પોતાની ધરીને અનુલક્ષીને $100\ rpm$ ની કોણીય ઝડપે ફરે છે. તેની સ્વિચ બંધ કરતાં $15\ s$ માં સ્થિર થાય છે, તો તે ....... પરિભ્રમણો બાદ સ્થિર થઈ હશે .View Solution
- 8બે વર્તૂળાકાર રિંગના દળોનો ગુણોત્તર $1 : 2$ અને વ્યાસોનો ગુણોત્તર $ 2 : 1$ છે. તો તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર શું હોય?View Solution
- 9આપેલ અક્ષને અનુલક્ષીને શરૂઆતમાં સ્થિર પડેલા પદાર્થની જડત્વની ચાકમાત્રા $1.5\, kg\, m^2$ છે.પદાર્થ પર ભ્રમણીય ગતિઊર્જા $1200\, J$ કરવા માટે તેના પર $20\, rad/s^2$ નો કોણીય પ્રવેગ તેની અક્ષ પર ....... $(\sec)$ સમય સુધી આપવો પડે.View Solution
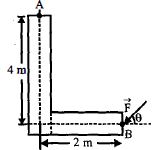
- 10આકૃતિમાં બતાવ્યા પ્રમાણે $L-$ આકારના પદાર્થના $B$ છેડે $40\, N$ બળ લાગે છે.ખૂણા $\theta$ દ્વારા બિંદુ $A$ પાસે ઉદભવેલી બળની મહત્તમ ચાકમાત્રા કેટલી હશે?View Solution