$4\,\Omega$ અવરોધ ધરાવતા એક તારને ખેંચીને તેની લંબાઈ બમણી કરવામાં આવે છે. આ ખેંચેલા તારનો અવરોધ............ $\Omega $ થશે.
AIPMT 2013, Medium
c
Resistance of a wire, \(R=\rho \frac{l}{A}=4\,\Omega\) .... \((i)\)
Resistance of a wire, \(R=\rho \frac{l}{A}=4\,\Omega\) .... \((i)\)
When wire is stretched twice, its new length be \(l\). Then
\(l^{\prime}=2 l\)
On stretching volume of the wire remains constant.
\(\therefore l A=l^{\prime} A^{\prime}\) where \(A^{\prime}\) is the new cross-sectional area
or \(\quad A^{\prime}=\frac{l}{l^{\prime}} A=\frac{l}{2 l} A=\frac{A}{2}\)
\(\therefore \quad\) Resistance of the stretched wire is
\(R^{\prime} =\rho \frac{l^{\prime}}{A^{\prime}} =\rho \frac{2 l}{(A / 2)}=4\, \rho \frac{l}{A}\)
\(=4(4 \,\Omega) =16\, \Omega (\text { Using }(\mathrm{i}))\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચેના પરિપથ માટે $x$ અને $y$ વચ્ચેનો સ્થિતિમાનનો તફાવત .........છે.View Solution
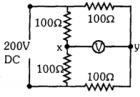
- 2$2 \Omega$ અવરોધ વાળો તાર $1 \,kW$,$220\, V$ નો પ્રવાહ નુ વહન કરે છે. તો તેની કાર્યક્ષમતા ....... $\%$View Solution
- 3એક $2\,W$ ના કાર્બન અવરોધ પર અનુક્રમે લીલા, કાળા, રાતા અને બ્રાઉન (કથ્થાઈ) રંગનો વર્ણ સંકેત છે. આ અવરોધમાંથી પસાર કરી શકાતો મહત્તમ પ્રવાહ કેટલા .............. $mA$ હશે?View Solution
- 4આપેલ સર્કિટનો પાવર કેટલા ............. $W$ થાય?View Solution
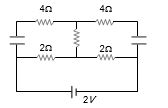
- 5આપેલ પોટેન્શિયોમીટરના તારનો અવરોધ $10\, \Omega$ છે. જ્યારે સ્લાઇડિંગ સંપર્ક પોટેન્શિયોમીટરના તારની વચ્ચે હોય ત્યારે $2\, \Omega$ ના અવરોધ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત કેટલો હશે?View Solution
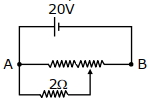
- 6$A B$ ની વચ્ચે $P.D.$ એટલે કે $V_A-V_B=........V$ છે.View Solution
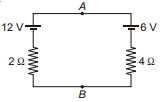
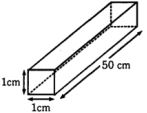
- 7એક ચતુષ્કોણ કાર્બન ટુકડાનું પરિમાણ $1.0\ cm \times 1.0\ cm \times 50\ cm$ છે. સૌ પ્રથમ બે ચોરસના છેડાઓ વચ્ચેનો અવરોધ માપવાનો અને પછી બે ચતુષ્કોણના છેડાઓ વચ્ચેનો અવરોધ માપવાનો છે. જો કાર્બનની અવરોધકતા $3.5 \times 10^{-5}$ $\Omega-m$, હોય તો અનુક્રમે અવરોધોનું મૂલ્ય........છે.View Solution
- 8$a$ અને $b$ ત્રિજ્યાના બે સમકેન્દ્રી અને સુવાહક નળાકારને $\sigma$ કન્ડક્ટીવિટી અને $V$ જેટલો અચળ સ્થિતિમાન તફાવત ધરાવતા પદાર્થ વડે અલગ કરેલા છે. પ્રતિ એકમ લંબાઈ એક નળાકારમાંથી બીજા નળાકારમાં પસાર થતો પ્રવાહ $..........$View Solution
- 9વિદ્યાર્થીને ચલિત વોલ્ટેજ સ્ત્રોત $V$, પરીક્ષણ અવરોધ $R_T=10\,\Omega$, બે સરખા ગેલ્વેનોમીટર $G_1$ અને $G_2$ અને બે વધારાના અવરોધ, $R _1=10\,M\Omega$ અને $R _2=0.001\,\Omega$ આપવામાં આવે છે.ઓહ્મના નિયમને ચકાસવા માટેનો પ્રયોગ કરવા માટે, સૌથી યોગ્ય પરિપથ કયો છે?View Solution
- 10$836\, watt$ ના હીટર દ્વારા $1\, litre$ પાણીનું તાપમાન $20\,^oC$ થી $40\,^oC$ કરતાં કેટલા ............ $sec$ સમય લાગે?View Solution
