A series combination of \(n_{1}\) capacitors each of capacitance \(C_{1}\) are connected to \(4 V\) source as shown in the figure.
Total capacitance of the series combination of the capacitors is
\(\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{1}}+\frac{1}{C_{1}}+\ldots \ldots \text { upto } n_{1} \text { terms }=\frac{n_{1}}{C_{1}}\)
or \(C_{s}=\frac{C_{1}}{n_{1}}.........(i)\)
Total energy stored in a series combination of the capacitors is
\(U_{s}=\frac{1}{2} C_{s}(4 V)^{2}=\frac{1}{2}\left(\frac{C_{1}}{n_{1}}\right)(4 V)^{2} \quad(\text { Using }(\mathrm{i})).........(ii)\)
A parallel combination of \(n_{2}\) capacitors each of capacitance \(C_{2}\) are connected to \(V\) source as shown in the figure.
Total capacitance of the parallel combination of capacitors is
\(C_{p}=C_{2}+C_{2}+\ldots \ldots \ldots+\text { upto } n_{2} \text { terms }=n_{2} C_{2}\)
or \(\quad C_{p}=n_{2} C_{2}.........(iii)\)
Total energy stored in a parallel combination of capacitors is
\(U_{p} =\frac{1}{2} C_{p} V^{2}\)
\(=\frac{1}{2}\left(n_{2} C_{2}\right)(V)^{2}.........\) (Using \((iii))...(iv)\)
According to the given problem,
\(U_{s}=U_{p}\)
Subst tuting the values of \(U_s,\) and \(U_p,\) from equations \((ii)\) and \((iv)\), we get
\(\frac{1}{2} \frac{C_{1}}{n_{1}}(4 V)^{2}=\frac{1}{2}\left(n_{2} C_{2}\right)(V)^{2}\)
or \(\quad \frac{C_{1} 16}{n_{1}}=n_{2} C_{2}\) or \(C_{2}=\frac{16 C_{1}}{n_{1} n_{2}}\)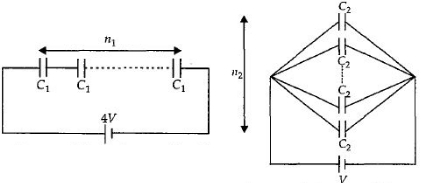
Download our appand get started for free
Similar Questions
- 1એક નળાકારીય કેપેસિટર પાસે $1.4\,cm$ અને $1.5 \,cm$ ત્રિજ્યાના અને $15\,cm$ લંબાઈ ધરાવતા બે નળાકારો છે. બાહ્ય નળાકારને જમીન સાથે જોડેલ છે. અને અંદરના નળાકારને $3.5\ \mu C$ નો વિદ્યુતભાર આપેલ છે. તંત્રનો કેપેસિટન્સ અને અંદરના નળાકારનો સ્થિતિમાન અનુક્રમે. . . . . .View Solution
- 2ડિફાઈબ્રીલેટરમાં $40\ \mu F$ કેપેસિટરને $3000\, V$ સુધી વિદ્યુતભારિત કરેલ છે.$2$ મિ.લિ સેંકડ અવધિના સ્પંદ દરમિયાન કેપેસિટરની સંગ્રહિત ઉર્જાને દર્દીં મારફતે મોકલવામાં આવે તો તે દર્દીંને આપવામાં આવેલ પાવર કેટલા ........$kW$ છે ?View Solution
- 3$R_1$ ત્રિજ્યાનો ઘન વાહક ગોળો $R_2$ ત્રિજ્યાના પોલા વાહક ગોળા વડે ઘેરાયેલો (આવત્ત) છે. તો આ સમૂહનો કેપેસિટન્સ ........ ના સમપ્રમાણમાં છે.View Solution
- 4બે અલગ કરેલા વાહકોને એક વાહકમાંથી બીજા વાહકમાં ઈલેકટ્રોન પસાર કરી ચાર્જ કરેલ છે. એક વાહકમાંથી બીજા વાહકમાં $6.25 \times 10^{15}$ ઈલેકટ્રોન પસાર કરતા $100\, V$ નો વિદ્યુત સ્થિતિમાન ઉત્પન્ન થાય તો તંત્રની કેપેસિટિ કેટલા ........$\mu F$ હશે ?View Solution
- 5સમાંતર પ્લેટ કેપેસિટરનું કેપેસિટન્સ ${C_0}$ છે,સાપેક્ષ પરમીટીવીટી ${\varepsilon _r}$ ધરાવતા અને બે પ્લેટ વચ્ચેના ચોથા ભાગની જાડાઇ ધરાવતો ડાઇઇલેકટ્રિક દાખલ કરતાં નવું કેપેસિટન્સ $C$ છે,તો $\frac{C}{{{C_0}}}=$View Solution
- 6જો ગોળાનો પરીઘ $2\,m$ હોય તો પાણીમાં ગોળાનું કેપેસીટન્સ...$pF$View Solution
- 7સમાન $1.5 \times 10^3\,NC ^{-1}$ ધરાવતા વીજક્ષેત્રમાં એક $6.0 \times 10^{-6}\,Cm$ દ્વિ-ધ્રુવીય ચાકમાત્રા ધરાવતા વીજ દ્વિ-ધ્રુવને એવી રીતે મૂકવામાં આવે છે કે જેથી દ્રી-ધ્રુવીય ચાકમાત્રા વીજક્ષેત્રની દિશામાં રહે. આ ક્ષેત્રમાં $180^{\circ}$ પર ફરતા દ્વિ-ધ્રુવ પર થતું કાર્ય $.........\,mJ$ હશે.View Solution
- 8$5\, \mu F$ કેપેસિટન્સ ધરાવતાં કેપેસિટરમાં ડાઇઇલેકિટ્રક પ્લેટ મૂકતાં વિદ્યુતસ્થિતિમાન $1/8^{th}$ માં ભાગનું થાય છે.તો ડાઇઇલેકિટ્રક નો ડાઇઇલેકિટ્રક અચળાંક કેટલો હશે?View Solution
- 9એક $8\; mC$ વિધુતભાર ઉગમબિંદુએ રહેલો છે. એક નાના $-2 \times 10^{-9} \;C$ વિધુતભારને $P (0,0,3\; cm )$ બિંદુથી $R (0,6\; cm , g \;cm )$ બિંદુએ થઈ $Q (0,4\; cm , 0),$ બિંદુએ લાવવા માટે કરેલું કાર્ય શોધો..View Solution
- 10સમાંતર પ્લેટો કેપિસિટરની બે ધાતુની પ્લેટો છે. એક પ્લેટને $+q$ વિદ્યુતભાર આપેલો છે. જ્યારે બીજાને જમીન સાથે જોડેલ છે. સંલગ્ન આકૃતિમાં દર્શાવ્યા પ્રમાણે $P, P_1$ અને $P_2$ બિંદુઓ લીધેલા છે. તો કયા બિંદુએ વિદ્યુત ક્ષેત્ર શૂન્ય નથી ?View Solution