$50\; kg$ દ્રવ્યમાન તથા $0.5\;m$ ત્રિજયાનો એક ઘન નળાકાર, તેની સમક્ષિતિજ અક્ષને અનુલક્ષીને મુકત રીતે પરિભ્રમણ કરી શકે છે. તેના પર વજનરહિત દોરી એવી રીતે વીંટાળેલી છે કે જેનો એક છેડો આ નળાકાર સાથે બાંધેલો છે અને બીજો છેડો મુક્ત રીતે લટકાવેલો છે. દોરી પર કેટલું તણાવબળ ($N$ માં) લગાડવામાં આવે કે જેથી કોણીય પ્રવેગ $2$ પરિભ્રમણ/સેકન્ડ$^2$ થાય?
AIPMT 2014, Medium
d
Here, mass of the cylinder, \(M = 50 kg\)
Here, mass of the cylinder, \(M = 50 kg\)
Radius of the cylinder,\( R = 0.5 m\)
Angular acceleration, \(\alpha = 2\,rev\,{s^{ - 2}}\)
\( = 2 \times 2\pi \,rad\,{s^{ - 2}} = 4\pi \,rad\,{s^{ - 2}}\)
Torque, \(\tau \, = TR\)
Moment of inertia of the solid cylinder about its
axis, \(I = \frac{1}{2}M{R^2}\)
\(\therefore \) Angular acceleration of the cylinder
\(\alpha = \frac{\tau }{I} = \frac{{TR}}{{\frac{1}{2}\,M{R^2}}}\)
\(T = \frac{{MR\alpha }}{2} = \frac{{50 \times 0.5 \times 4\pi }}{2} = 157\,N\)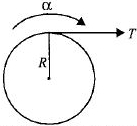
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m$ દળ અને $l$ લંબાઇ ધરાવતા સળિયાના મધ્યબિંદુ અને છેડાની મધ્યમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
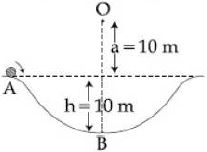
- 2એક $20\, g$ દળ ધરાવતા કણને આકૃતિમાં દર્શાવ્યા અનુસાર બિંદુ $B$ થી $h$ ઊંચાઈ એ આવેલા બિંદુ $A$ આગળથી $5\, m/s$ જેટલા પ્રારંભિક વેગ સાથે મુક્ત કરવામાં આવે છે. કણ ઘર્ષણ રહિત સપાટી પર સરકે છે. કણ જ્યારે બિંદુ $B$ આગળ પહોંચે છે, ત્યારે તેનું $O$ ની સાપેક્ષે કોણીય વેગમાન ....... $kg - m^2/s$ થશે.View Solution
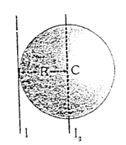
- 3વ્યાસ પર ગોળાની જડત્વની ચાકમાત્રા $ 40\ kg. m^2$ છે. કોઈ પણ સ્પર્શક પર જડત્વની ચાકમાત્રા શોધો.View Solution
- 4એક પોલો ગોળો તેની સંમિત અક્ષને સમાંતર (અનુલક્ષીને) એક સમતલ સપાટી ઉપર ગબડે છે તેની ચાકગતિ ઉર્જા અને કુલ ગતિઉર્જાનો ગુણોતર $\frac{x}{5}$ છે. $x$ નું મૂલ્ય. . . . . . .હશે.View Solution
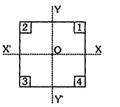
- 5આકૃતિમાં નિયમિત ચોરસ પ્લેટ દર્શાવેલી છે. જેના ખૂણા પરથી ચાર સમાન ચોરસ દૂર કરવામાં આવ્યા છે.ચોરસ $-1$ ને દૂર કરતાં $ C.M.$ ક્યાં મળશે ?View Solution
- 6લીસા સમક્ષિતિજ ટ્રેક પર $v$ ઝડપે ગતિ કરતી એ લાંબી ટ્રોલીનાં એક છેડે એક બાળક ઊભો રહેલો છે, જો, બાળકએ ટ્રોલીનાં બીજા છેડાં તરફ $u$ ઝડપે દોડવાનું શરૂ કરે છે તો તંત્ર (ટ્રોલી+બાળક) નું દ્રવ્યમાન કેન્દ્ર કેટલી ઝડપે ગતિ કરશે ?View Solution
- 7$M$ દળના અને $l$ લંબાઈના એક સ્લેન્ડર એકસમાન સળીયાને એક છેડાથી ધરીમાં એ રીતે જોડેલ છે કે જેથી તે ઊર્ધ્વતલમાં ભ્રમણ કરી શકે (આકૃતિ જુઓ). ધરી પર અવગણ્ય ધર્ષણ છે. મુક્ત છેડાને ઊર્ધ્વ દિશામાં ધરીની ઉપરની તરફ રાખેલ છે અને ત્યારબાદ તેને મુક્ત કરવામાં આવે છે. સળિયાનો કોણીય પ્રવેગ જ્યારે તે ઊર્ધ્વ સાથે $\theta$ ખુણો બનાવે ત્યારે કેટલો હશે?View Solution
- 8View Solutionપોલો અને ઘન ગોળાના દળ અને જડત્વની ચાકમાત્રા સમાન હોય,તો ત્રિજયાનો ગુણોત્તર કેટલો થાય?
- 9જો $\mathop {\rm{F}}\limits^ \to \, = \left( {\,4\hat i- 10\hat j\,} \right)$ અને $\mathop r\limits^ \to = \left( {\,5\hat i- 3\hat j\,} \right)$ હોય તો $\left( {\,\mathop \tau \limits^ \to = \mathop r\limits^ \to \times \mathop F\limits^ \to } \right)$ ની ગણતરી ... થાયView Solution
- 10$L$ લંબાઈ અને $ M$ દળના પાતળા સળિયાના એક છેડાથી $ L/3$ અંતરે રહેલાં બિંદુમાંથી પસાર થતી અને સળિયાને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
