$55\; kg$ અને $65 \;kg $ ના બે માણસ બોટના વિરુધ્ધ છેડે પર છે. બોટની લંબાઇ $3\;m$ અને દળ $100\;kg $ છે. $55\;kg$ નો માણસ ચાલીને $65\;kg $ ના માણસ પાસે બેસે છે. જો બોટ સ્થિર પાણીમાં હોય, તો તંત્રનું દ્રવ્યમાનકેન્દ્ર ($m$ માં) કેટલું ખસે?
AIPMT 2012, Easy
Download our app for free and get started
c
As no external force acts on the system, therefore centre of mass will not shift.
As no external force acts on the system, therefore centre of mass will not shift.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમતલ સપાટી પર ગબડતા પૈડાંનું કેન્દ્ર $v_{0}$ ઝડપથી ગતિ કરે છે. પૈડાંના કેન્દ્રના સમાન સ્તરમાં રહેલા પરિઘ પરના બિંદુનો વેગ $\sqrt{x}\, v_{0}$ હોય, તો $x$ નું મૂલ્ય કેટલું કેટલું હશે?View Solution
- 2$3\,kg$ દળ ની એેક તક્તી $5 \,m$ ઊંચાઈના એક ઢળતા સમતલ પરથી નીચે ગબડે છે. ઢળતા સમતલના તળિયે પહોંચતા તક્તીની રેખીય ગતિઊર્જા ........... $J$ હશે.View Solution
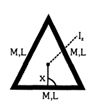
- 3ત્રણ સળિયાને સમબાજુ ત્રિકોણના સ્વરૂપમાં મૂકેલા છે. કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ અક્ષ પર જડત્વની ચાકમાત્રા ગણો. ( દળ $M$ અને લંબાઈ $L$ )View Solution
- 4$'m'$ દળ અને $R $ ત્રિજ્યાનો નળાકાર તેની અક્ષ પર '$\omega$' કોણીય વેગથી ઘર્ષણ વિના ચાકગતિ કરે છે. $ v$ વેગથી ગતિ કરતો $m$ દળનો કણ તેની સાથે અથડાઇને તેની રીમ પર ચોટી જાય છે. આઘાત બાદ નળાકારનો કોણીય વેગ ગણો.View Solution
- 5$m_1 = fM$ અને $m_2 = (1 -f)\,M\,(f < 1 )$ દળના બે સૂક્ષ્મદળો બાહ્ય અવકાશમાં (બીજી કોઈ વસ્તુની ગુરુત્વઅસરથી દૂર) એકબીજાથી $R$ અંતરે છે. તે બંને તેમના દ્રવ્યમાન કેન્દ્ર ને અનુલક્ષીને વર્તુળાકાર કક્ષા માં $m_1$ એ $\omega _1$ અને $m_2$ એ $\omega _2$ કોણીય વેગથી ગતિ કરે છે.તો આ કિસ્સામાં કોણીય વેગ .....View Solution
- 6$\mathop r\limits^ \to = (3\hat i + 2\hat j + 3\hat k)\,m$ બિંદુ પર બળ $\mathop F\limits^ \to = (2\hat i - 3\hat j + 4\hat k)\;N$ લાગતા, ઉગમબિંદુને અનુલક્ષીને ટોર્ક કેટલું થાય?View Solution
- 7$1\,\,kg$ અને $3\,\, kg$ દળ ધરાવતાં બે કણોના સ્થાનસદિશ અનુક્રમે $\hat i\,\, + \,2\hat j\,\, + \,\,\hat k\,\,$અને$\,\, - 3\hat i\,\, - \,2\hat j\,\, + \,\,\hat k$ છે. આ કણોના તંત્રના દ્રવ્યમાન કેન્દ્રનું સ્થાનસદિશ ...... થાય?View Solution
- 8$L$ લંબાઈ ધરાવતા અરેખીય ઘનતા ધરાવતા સળિયાની ઘનતા $\rho(\mathrm{x})={a}+{b}\left(\frac{\mathrm{x}}{\mathrm{L}}\right)^{2}$ મુજબ આપવામાં આવે છે જ્યાં $a$ અને $ {b}$ અચળાંક અને $0 \leq \mathrm{x} \leq \mathrm{L}$ છે.સળિયાના દ્રવ્યમાન કેન્દ્ર માટે $x$ નું મૂલ્ય કેટલું હોવું જોઈએ?View Solution
- 9View Solutionઘન ગોળાને મુક્ત અવકાશમાં ચાકગતિ કરે છે. જો ગોળાની ત્રિજ્યા વધારવામાં આવે અને તેનું દળ તેટલું જ રાખવામાં આવે તો નીચેનામાંથી .... ને અસર થશે નહિ.
- 10$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી એક પાતળી વર્તુળાકાર રીંગ સમક્ષિતિજ સમતલમાં, સમતલને લંબ અક્ષને અનુલક્ષીને $2 \,rads^{-1}$ ના કોણીય વેગથી ભ્રમણ કરે છે. જો બે સમાન $m$ દળ વાળા પદાર્થોને હળવેકથી રિંગના વ્યાસના વિરુધ્ધ છેડાઓ જોડવામાં આવે તો હવે રીંગ .............. ( $rads^{-1}$ માં) ના કોણીયવેગ સાથે પરિભ્રમણ કરશે.View Solution