$\mathop r\limits^ \to = (3\hat i + 2\hat j + 3\hat k)\,m$ બિંદુ પર બળ $\mathop F\limits^ \to = (2\hat i - 3\hat j + 4\hat k)\;N$ લાગતા, ઉગમબિંદુને અનુલક્ષીને ટોર્ક કેટલું થાય?
AIPMT 1995, Medium
c
Torque of a Force \(\vec{F}\) acting on a point with position vector \(\vec{r}\) is given by:
Torque of a Force \(\vec{F}\) acting on a point with position vector \(\vec{r}\) is given by:
\(\vec{\tau}=\vec{r} \times \vec{F}\)
To, we can find Torque by finding the cross product of \(\vec{r}\) and \(\vec{F}\)
We have:
\(\vec{r}=3 \hat{\imath}+2 \hat{\jmath}+3 \hat{k} m\)
\(\vec{F}=2 \hat{\imath}-3 \hat{\jmath}+4 \hat{k} N\)
So, torque will be:
\(\vec{\tau}=\left|\begin{array}{ccc}{\hat{\imath}} & {\hat{\jmath}} & {\hat{k}} \\ {3} & {2} & {3} \\ {2} & {-3} & {4}\end{array}\right|\)
\(\Longrightarrow \vec{\tau}=\hat{\imath}((2)(4)-(-3)(3))-\hat{\jmath}((3)(4)-(2)(3))+\hat{k}((3)(-3)-(2)(2))\)
\(\Longrightarrow \vec{\tau}=\hat{\imath}(8+9)-\hat{\jmath}(12-6)+\hat{k}(-9-4)\)
\(\Longrightarrow[\vec{\tau}=17 \hat{\imath}-6 \hat{\jmath}-13 \hat{k}, N m]\)
This is the torque of the force acting about Origin.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
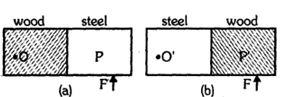
- 1આકૃતિમાં મીટર પટ્ટીનો અડધો ભાગ લાકડાનો અને અડધો સ્ટિલનો બનેલો છે. લાકડાનો ભાગ $O$ પર કિલકિત કરેલો છે. બળ $ F$ સ્ટીલના ભાગે આપવામાં આવે છે. આકૃતિમાં $(b)$ માં સ્ટીલનો ભાગ $ O$ પર કિલકિત કરેલો છે. અને તેટલું જ લાકડાના ભાગ પર આપવામાં આવે છે.View Solution
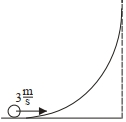
- 2સમાન ધનતાનો એક પોલો ગોળાકાર દડો $3\,m/s$ પ્રારંભિક વેગથી આકૃતિમા દર્શાવ્યા મુજબ વક્ર સપાટી પર ગબડે છે. પ્રારંભિક સ્થાનને અનુલક્ષીને તેણે પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ $........cm$ હશે.$(g=10\,m / s ^2)$ લો.View Solution
- 3$M $ દળ અને $ l $ લંબાઇના ચાર પાતળા સળિયા એક ચોરસ ફ્રેમની રચના કરે છે. આ ચોરસના સમતલને લંબ અને ફ્રેમના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 4એક લિસી સપાટીવાળો $A$ ગોળો એક ઘર્ષણરહિત સમક્ષિતિજ પર કોણીય વેગ $\omega$ અને તેનું દ્રવ્યમાન કેન્દ્ર $v $ વેગ થી ગતિ કરે છે. તે પોતાના જેવા જ બીજા સ્થિર ગોળા $B$ સાથે સ્થિતિસ્થાપક સંઘાત અનુભવે છે. જો સંઘાત પછી તેના કોણીય વેગ અનુક્રમે $\omega_A$ અને $\omega_B$ છે બધી જગ્યાએ ઘર્ષણ અવગણઈએ તો નીચેમાંથી શું સાચું છે ?View Solution
- 5એક $M$ દળ અને $R$ ત્રિજયાની તકતી તેના કેન્દ્રમાથી પસાર થતી સમક્ષિતિજ અક્ષને અનુલક્ષીને $\omega$ કોણીય વેગથી ફરે છે. હવે જો $m$ દળનો એક ટુકડો તેમાંથી તૂટીને ઉપરની શિરોલંબ દિશામાં ફેકાઈ જાય તો તકતીનો નવો કોણીય વેગ કેટલો થાય ?View Solution
- 6એક પાતળી વર્તુળાકાર રિંગ જેનું દળ $M$ અને ત્રિજ્યા $R$ તેની ધરી પર અચળ કોણીય વેગ $\omega $ થી પરિભ્રમણ કરે છે. રિંગનાં વ્યાસના બિંદુઓ પર $m$ દળનાં એવા બે પદાર્થોને ધીમેથી જોડવામાં આવે છે. હવે રિંગ કેટલા કોણીય વેગથી ગતિ કરશે?View Solution
- 7એક $3m$ દળનો પ્રક્ષિપ્ત તેના પથના મહત્તમ બિંદુએ ફૂટે છે અને તે ત્રણ સમાન ભાગોમાં વહેંચાય છે. જેમાંનો એક ભાગ તેના પથ (માર્ગ) પર પાછો ફરે છે. બીજો સ્થિર સ્થિતિએ જાય છે. જ્યારે ત્રીજો ભાગ જમીન પર ઉતરાણ કરે ત્યારે પ્રક્ષિપ્ત બિંદુથી તેનું અંતર ......... $m$ હશે. (વિસ્ફોટ ન થયો હોય તે સમયે પ્રક્ષિપ્ત અવધિ $100 m$ હતી)View Solution
- 8$R$ ત્રિજ્યા અને $9M$ દળની વર્તુળાકાર તકતીમાંથી સમકેન્દ્રિય રહેલ $\frac{R}{3}$ ત્રિજ્યા અને $M$ દળની નાની તકતીને દૂર કરવામાં આવે છે. બાકી રહેલી તકતીની તકતીના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 9દરેક $M$ દળ ધરાવતા ત્રણ એક સમાન ગોળાઓને કાટકોણ ત્રિકોણના ખૂણાઓ (શિરોબિંદુ) પર મૂકવામાં આવ્યા છે. કાટકોણ ત્રિકોણની એકબીજાને લંબ બાજુ $3\,m$ ની છે. આ બે એકબીજાને લંબ બાજુનાં અંતઃ છેદને ઉગમ બિંદુ તરીકે લઈ દ્રવ્યમાન કેન્દ્રના સ્થાન સદિશના માનાંક $\sqrt{x} m$ છે, તો $x=........$ થશે.View Solution
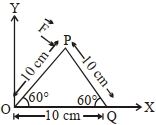
- 10આકૃતિમાં દર્શાવેલ ત્રિકોણાકાર પ્લેટ પર રહેલ $P$ બિંદુ પર $\overrightarrow{ F }=4 \hat{ i }-3 \hat{ j }$ જેટલું બળ લાગે છે. તો $P$ બિંદુ પર $O$ અને $Q$ બિંદુની સાપેક્ષે લાગતું ટોર્ક કેટલું હશે?View Solution