$[$આપેલ છે :${R}=8.31\, {~J} \,{~K}^{-1} \,{~mol}^{-1} ; \log 6.36 \times 10^{-3}=-2.19$ $\left.10^{-4.79}=1.62 \times 10^{-5}\right]$
${K}_{700}=6.36 \times 10^{-3} {~s}^{-1}$
${~K}_{600}=x \times 10^{-6} {~s}^{-1}$
${E}_{{a}}=209 {~kJ} / {mol}$
Applying ;
$\log \left(\frac{{K}_{{T}_{2}}}{{~K}_{{T}_{1}}}\right)=\frac{-{E}_{{a}}}{2.303 {R}}\left(\frac{1}{{~T}_{2}}-\frac{1}{{~T}_{1}}\right)$
$\log \left(\frac{{K}_{700}}{{~K}_{600}}\right)=\frac{-{E}_{{a}}}{2.303 {R}}\left(\frac{1}{700}-\frac{1}{600}\right)$
$\log \left(\frac{6.36 \times 10^{-3}}{{~K}_{600}}\right)=\frac{+209 \times 1000}{2.303 \times 8.31}\left(\frac{100}{700 \times 600}\right)$
$\log \left(6.36 \times 10^{-3}\right)-\log {K}_{600}=2.6$
$\Rightarrow \log {K}_{600}=-2.19-2.6=-4.79$
$\Rightarrow {K}_{600}=10^{-4.79}$
$=1.62 \times 10^{-5}$
$=16.2 \times 10^{-6}$
$=x \times 10^{-6}$
$\Rightarrow {x}=16$
Download our appand get started for free
Similar Questions
- 1રેડિયોએક્ટિવ ક્ષયમાં એક યુરેનિયમ પરમાણુનુ એક લેડ પરમાણુમાં રૂપાંતર થાય છે. જો ચંદ્ર પરના એક ખડકના નમૂનામાં યુરેનિયમ તથા લેડના પરમાણુઓની સંખ્યા સમાન હોય તથા યુરેનિયમ માટે $t_{1/2} = 4.5 \times 10^9$ વર્ષ હોય તો ખડકનુ આયુષ્ય .... થશે. છેView Solution
- 2$100\,^oC$ તાપમાને પ્રથમ ક્રમની એક પ્રક્રિયાનો વેગ અચળાંક $K= 1.5 \times 10^{-2}\,s^{-1}$ છે. જો પ્રકિયકની શરૂઆતની સાંદ્રતા $100\, mol\,L^{-1}$ હોય, તો $10\,\min$ પછી પ્રક્રિયકની સાંદ્રતા કેટલી થશે ?View Solution
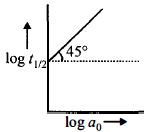
- 3પ્રક્રિયા $A \to$ નીપજો માટે $log\,t_{1/2}$, વિરુદ્ધ $log\,a_0$ નો આલેખ આકૃતિમાં દર્શાવ્યો છે. જો $A$ ની શરૂઆતની સાંદ્રતા $a_0,$, વડે દર્શાવવામાં આવે તો પ્રક્રિયાની ક્રમ જણાવો.View Solution
- 4પ્રથમક્રમની પ્રક્રિયાને અનુસરીને એક સંયોજન $A$,સંયોજન $B$ સાથે પ્રક્રિયા કરે છે, જેનો વેગ અચળાંક $2,011 \times 10^{-3}\,s^{-1}$ છે.સંયોજન $A$ ના $7\,g$ ને $28$ માં ઘટતા લાગતો સમય (સેકન્ડોમાં) $.....$ છે.(નજીકનો પૂર્ણાક) $[\log 5=0.698, \log 7=0.845, \log 2=0.301]$View Solution
- 5એક ફ્લાસ્ક સંયોજનો $AB$ અને $XY$ નુ મિશ્રણ ધરાવે છે.તેઓને ગરમ કરતા બંનેનુ વિઘટન પ્રથમ કમની પ્રકિયા મુજબ થાય છે. જો $AB$ અને $XY$ ના અર્ધઆયુષ્ય સમય અનુક્રમે $30\,\min$ અને $10\,\min$ હોય, તો $AB$ ની સાંદ્રતા $XY$ ની સાંદ્રતા કરતા ચાર ગણી થતા ....... $\min.$ લાગશે. ($AB$ અને $XY$ ની શરૂઆતની સાંદ્રતા સમાન ગણો)View Solution
- 6$A$ તથા $B$ વચ્ચેની પ્રક્રિયામાં $A$ ના સંદર્ભમાં પ્રક્રિયાક્રમ $2$ છે. તથા $B$ ના સંદર્ભમાં પ્રક્રિયાક્રમ $3$ છે. જો $A$ તથા $B$ બંનેની સાંદ્રતા બમણી કરવામાં આવે તો પ્રક્રિયાક્રમ .............. ના ગુણકથી વધશે.View Solution
- 7પ્રથમ, દ્વિતીય અને તૃતીય ક્રમના ત્રણ પ્રક્રિયા માટેના દર અચળાંક આંકડામાં સમાન હોય છે. પ્રક્રિયકની સાંદ્રતા સમાન અને $1\,M$ કરતા વધારે હોય તો આ ત્રણ પ્રક્રિયાનો દર માટે ગતિમાં કયું એક સાચું છે?View Solution
- 8View Solutionસક્રિયકરણ ઉર્જાએ .......... છે.
- 9$H_2O_2$ ના વિઘટનની પ્રક્રિયાનો વેગ અચળાંક $3.66 \times 10^{-3}\,s^{-1}$ છે. જો $H_2O_2$ ની શરૂઆતની સાંદ્રતા $0.882\, M$ હોય, તો ........ $\sec$ એ તેની સાંદ્રતા $0.600\,M$ થશે.View Solution
- 10પ્રકિયા માટે સક્રિયકરણ ઉર્જા $\mathrm{E}_{\mathrm{a}}=0$ અને $200\; \mathrm{K}$ તાપમાને અચળ વેગ $1.6 \times 10^{6} \;\mathrm{s}^{-1} .$ $400\; \mathrm{K}$ તાપમાને અચળ વેગે વાયુ ના અચળાંક નું મૂલ્ય શું હશે ?View Solution
$\mathrm{R}=8.314\; \mathrm{JK}^{-1} \mathrm{mol}^{-1}$
