$90 \%$ કાર્યક્ષમતા ઘરાવતું ટ્રાન્સફોર્મર $200 \;V $ અને $3\; kW$ ના પાવર સ્ત્રોત પર કાર્ય કરે છે. જો ગૌણ ગુંચળાનો પ્રવાહ $6\;A$ હોય, તો ગૌણ ગુંચળાનો વોલ્ટેજ અને પ્રાથમિક ગુંચળામાં પ્રવાહ અનુક્રમે કેટલા હશે?
AIPMT 2014, Medium
b
Here,
Here,
Efficiency of the transformer, \(\eta=90 \%\)
Input power, \(P_{\mathrm{in}}=3\, \mathrm{kW}=3 \times 10^{3}\, \mathrm{W}=3000\, \mathrm{W}\)
Voltage across the primary coil, \(V_{p}=200\, \mathrm{V}\)
Current in the secondary coil, \(I_{s}=6\, \mathrm{A}\) As \(P_{\text {in }}=I_{p} V_{p}\)
\(\therefore\) Current in the primary coil,
\(I_{p}=\frac{P_{\text {in }}}{V_{p}}=\frac{3000 \mathrm{W}}{200 \mathrm{V}}=15\, \mathrm{A}\)
Efficiency of the transformer,
\(\eta=\frac{P_{\text {out }}}{P_{\text {in }}}=\frac{V_{s} I_{s}}{V_{p} I_{p}}\)
\(\therefore \quad \frac{90}{100}=\frac{6 V_{s}}{3000}\) or \(V_{s}=\frac{90 \times 3000}{100 \times 6}=450\, \mathrm{V}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$5 \mathrm{~m}$ લંબાઈના એક સમક્ષિતિજ સીધો તાર કે જે પૂર્વથી પશ્રિમ દિશામાં લંબાયેલો (ખેંચાયેલો) છે એ $0.60 \times 10^{-4} \mathrm{~Wb} \mathrm{~m}^{-2}$ જેટલા પૃથ્વીના ચુંબકીય ક્ષેત્રના સમક્ષિતિજ ધટકથી કાટકોણે પતન કરે છે. તારમાં પ્રેરીત $emf$ નું તત્કાલીન મૂલ્ય__________$\times 10^{-3} \mathrm{~V}$છે.View Solution
- 2એક વિદ્યુત મોટર $50 \;V$ ના વિદ્યુતસ્થિતિમાન અને $12 \;A$ વિદ્યુતપ્રવાહ પર ચાલે છે. જો મોટરની કાર્યક્ષમતા $30 \%$ હોય તો મોટરના ગૂંચળાનો અવરોધ કેટલો હશે?View Solution
- 3ટ્રાન્સફોર્મરના ગૌણ ગૂંચળામાં $AC$ વોલ્ટેજ ઉત્પન્ન થવાનું કારણ નીચે પૈકી કયું છે?View Solution
- 4બધા પરિપથમાં સમાન બેટરી,ઇન્ડકટર અને અવરોધ છે,બેટરીમાંથી પસાર થતો પ્રવાહ $(i)$ કળ બંધ કરતાં તરત જ $(ii)$ કળ બંધ કરતાં ઘણા સમય પછી , પ્રવાહ ઉતરતા ક્રમમાં નીચે પૈકી કયો થાય?View Solution
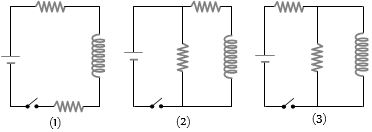
- 5$L-R$ પરિપથને ચાર્જ કરતાં તેનો પ્રવાહ $4\, sec$ માં $ \frac{3}{4} ^{th} $ ગણો થાય છે.તો $L-R$ પરિપથનો સમય અચળાંક કેટલો થાય?View Solution
- 6View Solutionનીચેનામાંથી શેમાં એડી પ્રવાહનો ઉપયોગ થતો નથી.
- 7$2\,mH$ અને $8\,mH$ આત્મ-પ્રેરકત્વ ઘરાવતાં બે ગૂંચળાઓ એકબીજાની નજીક એવી રીતે ગોઠવેલાં છે કે જેથી એક ગૂંચળાનું ફ્લકસ બીજા ગૂંચળા સાથે સંપૂર્ણપણે સંકળાય છે. આ બે ગૂંચળા વચ્ચેનું અન્યોન્ય પ્રેરકત્વ ......... $ mH$ હશે.View Solution
- 8View Solutionલેન્ઝનો નિયમ કયાં નિયમના સંરક્ષણ પરથી મેળવેલ છે.
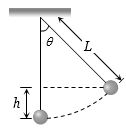
- 9$L$ લંબાઇ ધરાવતું સાદું લોલક ચુંબકીયક્ષેત્ર $B$ માં લંબ રહીને $ 2\theta $ ખૂણે દોલનો કરે છે,તો મહત્તમ $emf$ કેટલો થાય?View Solution
- 10View Solutionટ્રાન્સફોર્મરનો કોર લેમીનેટેડ કરવાથી કયો વ્યય ઓછો થાય?
