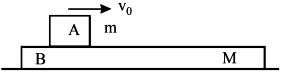
$A$ અને $B$ બ્લોકના દળ અનુક્રમે $m$ અને $M$ છે.$A$ અને $B$ વચ્ચે અચળ ઘર્ષણ બળ $F$ છે અને $B$ એ સરળ સમક્ષિતિજ સપાટી પર લપસી શકે છે.$B$ સ્થિર હોય ત્યારે $A$ ને વેગથી ગતિ આપવામાં આવે છે. જ્યારે બંને સમાન વેગથી ગતિ કરે ત્યારે $B$ ની સાપેક્ષમાં $A$ દ્વારા કપાયેલ અંતર .......

Diffcult
d
(d)
(d)
For the blocks \(A\) and \(B\) \(FBD\) as shown below
Equations of motion
\(a_A=\frac{F}{M}(\text { in }-x \text { direction })\)
\(a_B=\frac{F}{M}(\text { in }+x \text { direction })\)
Relative acceleration, of A w.r.t. B,
\(a_{A, B} =a_A-a_B=-\frac{F}{m}-\frac{F}{M}\)
\(=-F\left(\frac{M+m}{M m}\right) \text { (along }-x \text { direction) }\)
Initial relative velocity of Aw.r.t. \(B , u _{ AB }= v _0\) using equation \(v ^2= u ^2+2 a\)
\(0= v _0^2-\frac{2 F ( m + M ) S }{ Mm } \Rightarrow S =\frac{ Mmv _0^2}{2 F ( m + M )}\)
i.e., Distance moved by A relative to \(B\)
\(S _{ AB }=\frac{ Mmv _0^2}{2 F ( m + M )}\)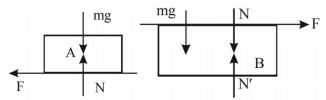
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બરફના બ્લોકને $\theta=45^°$ ઢાળવાળા રફ ઢાળ પરથી નીચે આવતા લાગતો સમય એ સમાન ઘર્ષણરહિત ઢાળ પરથી નીચે આવતા લાગતા સમય કરતાં બમણો હોય તો બ્લોક અને ઢાળ વચ્ચેનો ઘર્ષણાંક કેટલો હશે?View Solution
- 2નિયમિત એવી ભારે સાંકળ સમક્ષિતિજ ટેબલની સપાટી પર પડેલી છે. જો સાંકળ અને ટેબલની સપાટી વચ્ચેનો ઘર્ષણાંક $0.25$ હોય, તો સાંકળની કુલ લંબાઇનો કેટલા $\%$ ભાગ ટેબલની ધાર આગળ લટકતો રહી શકે?View Solution
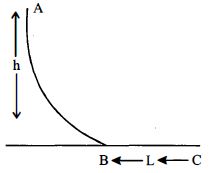
- 3આકૃતિ માં દર્શાવ્યા પ્રમાણે $m$ દળનો એક નાનો દડો $A$ સ્થાને થી $v_0$ ઝડપે શરૂ કરીને ઘર્ષણરહિત માર્ગ $AB$ પર ગતિ કરે છે. માર્ગ $BC$ ઘર્ષણાંક $\mu $ ધરાવે છે. દડો $L$ અંતર કાપીને $C$ પર સ્થિર થાય છે, તો $L$ કેટલું હશે?View Solution

- 4એક બીજાથી $1.5 \mathrm{~m}$ દૂર રહેલા બે પાટાઓ પર એક ટ્રેન $12 \mathrm{~m} / \mathrm{s}$ ની ઝડપે ગતિ કરે છે. $400 \mathrm{~m}$ ત્રિજયાનો વક્ર સલામત બને તે માટે બહારના પાટાની અંદરના પાટાની સાપેક્ષ ઉંચાઈ_____ $\mathrm{cm}$ વધારવી પડે. ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ આપેલ છે.) :View Solution
- 5View Solutionબે સપાટીઓ વચ્ચેનો સ્થિત ઘર્ષણ એ .......
- 6$2kg $ નો બ્લોક $30^o$ ના ઢાળ પર પડેલો છે જો સ્થિત ઘર્ષણાંક $0.7$ હોય તો ઘર્ષણબળ ....... $N$ થાય.View Solution
- 7$30^o$ ખૂણાવાળા ઢાળ પર $10\, kg $ નો બ્લોક મૂકતાં તે માત્ર ગતિની શરૂઆત કરતો હોય,તો ગતિક ઘર્ષણ બળ ....... $kg\, wt$ થશે.View Solution
- 8આકૃતિ માં દર્શાવ્યા પ્રમાણે $m$ દળનો એક નાનો દડો $A$ સ્થાને થી $v_0$ ઝડપે શરૂ કરીને ઘર્ષણરહિત માર્ગ $AB$ પર ગતિ કરે છે. માર્ગ $BC$ ઘર્ષણાંક $\mu $ ધરાવે છે. દડો $L$ અંતર કાપીને $C$ પર સ્થિર થાય છે, તો $L$ કેટલું હશે?View Solution
- 9View Solutionજ્યારે બે સપાટી લુબ્રિકન્ટ કરેલી હોય તો તે
- 10$4m$ ત્રિજયા ધરાવતા સમતલ રોડ પર કારની મહત્તમ સલામત ઝડપ $4.9\;m/s$ છે.રોડ અને ટાયર વચ્ચેનો ઘર્ષણાંક કેટલો હશે?View Solution
