$2kg $ નો બ્લોક $30^o$ ના ઢાળ પર પડેલો છે જો સ્થિત ઘર્ષણાંક $0.7$ હોય તો ઘર્ષણબળ ....... $N$ થાય.
IIT 1980, Medium
Download our app for free and get started
a
(a) Limiting friction \({F_l} = \mu \;mg\cos \theta \)
(a) Limiting friction \({F_l} = \mu \;mg\cos \theta \)
\({F_l} = 0.7 \times 2 \times 10 \times \cos 30^\circ = 12\;N\)(approximately)
But when the block is lying on the inclined plane then component of weight down the plane \( = mg\sin \theta \) \( = 2 \times 9.8 \times \sin 30^\circ = 9.8\;N\)
It means the body is stationary, so static friction will work on it
\(\therefore \) Static friction \(=\) Applied force \(= 9.8 \,N\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
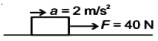
- 1આકૃતિમાં દર્શાવ્યા મુજબ $10\, kg$ દળનો એક બ્લોક એ $2 \,m / s ^2$ પ્રવેગ સાથે સમક્ષિતિજ ખરબચડી સપાટી પર ગતિ કરી રહ્યો છે, તો ગતિક ઘર્ષણાંકનું મુલ્ય છે.View Solution
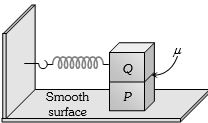
- 2આકૃતિ માં દર્શાવ્યા પ્રમાણે $P$ અને $Q$ બ્લોક સ્પ્રિંગ થી જોડેલા છે બંને બ્લોક એક સાથે સરળ આવર્ત ગતિમાં $A$ એમ્પ્લીટુડથી ગતિ કરે તો $P$ અને $Q$ વચ્ચેનું મહત્તમ ઘર્ષણબળ કેટલું હશે?View Solution
- 3એક કાર અચળ ઝડપે $0.2 \,km$ ની ત્રિજ્યાના સમક્ષિતિજ વર્તુળાકાર રસ્તા પર ગતિ કરી રહી છે. કારના ટાયર અને રસ્તા વચ્ચેનો ઘર્ષણ $0.45$ છે, તો કારની મહત્તમ ઝડપ .............. $m / s$ હોઈ શકે છે [ $g=10 \,m / s ^2$ લો]View Solution
- 4એક કાર $R$ ત્રિજયાના વક્ર માર્ગ પર ગતિ કરે છે. માર્ગનો ઢાળ $\theta $ કોણ જેટલો છે. કારના ટાયર અને માર્ગ વચ્ચેનો ઘર્ષણાંક ${\mu _s}$ છે. આ માર્ગ પર મહત્તમ સલામત વેગ કેટલો હશે?View Solution
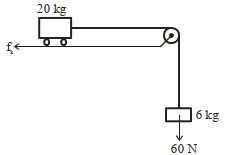
- 5આકૃતિમાં દર્શાવ્યા મુજબ એક બ્લોક અને ટ્રોલીના તંત્રને ધ્યાનમાં લો. જો ટ્રોલી અને સપાટી વચ્ચેનો ગતિક ઘર્ષણાંક $0.04$ હોય તો તંત્રનો $\mathrm{ms}^{-2}$ માં પ્રવેગ__________છે.(દોરીનું દળ અવગણો)View Solution
- 6$W$ વજન વાળા પદાર્થને શિરોલંબ સપાટી પર સ્થિર રાખવા $F$ બળ લાગવું પડે તો $F$ નું ન્યૂનતમ મૂલ્ય કેટલું હશે?View Solution
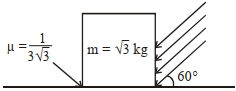
- 7$\frac{1}{3 \sqrt{3}}$ જેટલા ઘર્ષણાંક ધરાવતી સમક્ષિતીજ ખરબચડી સપાટી પર $3\, kg$ દળ ધરાવતાં ચોસલાને આકૃતિમાં દર્શાવ્યા મુજબ ગોઠવવામાં આવ્યો છે. દર્શાવ્યા અનુસાર સમક્ષિતીજ સાથે $60°$ કોણ રચતા ઉર્ધ્વ સપાટી પર જરૂરી બળનું ઓછામાં ઓછું મૂલ્ય $3x$ છે કે જેથી તે ચોસલું ખસી ના શકે. $3x$ નું મૂલ્ય ......... હશે.View Solution
$\left[g=10 m / s ^{2} ; \sin 60^{\circ}=\frac{\sqrt{3}}{2} ; \cos 60^{\circ}=\frac{1}{2}\right]$
- 8એક ઘર્ષણરહિત ટેબલ પર બ્લોક $B$ છે અને તણા પર બીજો બ્લોક $A$ છે જો $A$ અને $B$ વચ્ચે નો ઘર્ષણાક $\mu $ $A$ ને $B$ વચ્ચે ગતિ ની શરૂઆત કરવા $B$ ને કેટલો મહતમ પ્રવેગ આપવો પડશે?View Solution
- 9$400\,ms ^{-1}$ ની સમક્ષિતિજ ઝડપથી ગતિ કરતી $0.1\,kg$ દળની એક બુલેટ (ગોળી) ખરબચડી સમક્ષિતિજ સપાટી પર રાખેલ $3.9\,kg$ દળના બ્લોક સાથે અથડાય છે. બુલેટ આ બ્લોકમાં સ્થિર થઈ અને સંયુક્ત તંત્ર સ્થિર થાય તે પહેલા $20\,m$ અંતર કાપે છે.બ્લોક અને સપાટી વચ્ચેનો ધર્ષણાંક $......$ છે. (આપેલ $g =10\,m / s ^2$ )View Solution
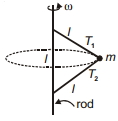
- 10આપેલ આકૃતિમાં, એક $m$ દળનો ગોળો બે સમાન લંબાઈની દોરીઓ વડે જોડેલ છે. જો સળીયાના કોણીય વેગ $\omega$ સાથે ફેરવામાં આવે છે, તો પછીView Solution
