$a$ બાજુવાળા ચોરસના કેન્દ્રની ઉપર $a/2$ અંતરે $q$ વિદ્યુતભાર મૂકતાં સમઘનની કોઇ એકબાજુમાંથી કેટલુ ફલ્કસ પસાર થાય?
Easy
Download our app for free and get started
d
(d) An imaginary cube can be made by considering charge \(q\) at the centre and given square is one of it's face.
So flux from given square (i.e. one face) \(\varphi = \frac{q}{{6{\varepsilon _0}}}\)
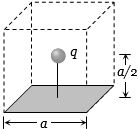
(d) An imaginary cube can be made by considering charge \(q\) at the centre and given square is one of it's face.
So flux from given square (i.e. one face) \(\varphi = \frac{q}{{6{\varepsilon _0}}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$9.1 \times 10^6\ N/C$ ના વિદ્યુતક્ષેત્રમાં એક ઈલેક્ટ્રોનનો દાખલ કરતાં ઉદભવતો પ્રવેગ ..... $ms^{-2}$ છે.View Solution
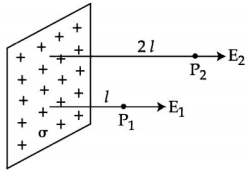
- 2આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરોView Solution
- 3View Solutionશૂન્યાવકાશમાં કોઈ બિંદુએ વિદ્યુતક્ષેત્રની તીવ્રતા
- 4$h$ ઊંચાઈ અને $R$ બેજની ત્રિજ્યા ધરાવતા શંકુને $\vec E$ વિદ્યુતક્ષેત્રમાં એવી રીતે મૂકવામાં આવે છે કે જેથી વિદ્યુતક્ષેત્ર બેજને સમાંતર રહે.તો શંકુમાં દાખલ થતું વિદ્યુત ફ્લક્સ કેટલું હશે?View Solution
- 5વિદ્યુતભાર $Q$ એ ચોરસનાં બે વિરુદ્ઘ શિરોબિંદુઓ પર મૂકેલો છે.બાકીનાં બે શિરોબિંદુઓ પર $-q$ જેટલો વિદ્યુતભાર છે.જો વિદ્યુતભાર $Q$ પર લાગતુ પરિણામી બળ શૂન્ય હોય,તો $\frac{Q}{q}$= ______View Solution
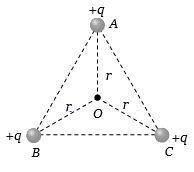
- 6સમબાજુ ત્રિકોણ $ABC$ ના દરેક શિરોબિંદુ પર $ + \,q$ વિજભાર મૂકેલા છે તો $O$ બિંદુ પાસે વિદ્યુતક્ષેત્રની તીવ્રતા કેટલી થાય?View Solution
- 7View Solutionએક કુલંબ વિદ્યુતભારમાં રહેલા ઇલેક્ટ્રોન....
- 8$\overrightarrow{ p }$ ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલના કેન્દ્રથી $r$ અંતરે વિષુવવૃતીય સમતલ પર રહેલા બિંદુ આગળ વિધુતક્ષેત્ર ........... મળે ($r >>$ ડાઈપોલના બે વિધુતભાર વચ્ચેનું અંતર,$\varepsilon_{0}$ મુક્ત અવકાશની પરમિટિવિટી)View Solution
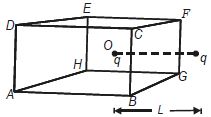
- 9$L$ બાજુવાળા સમઘન $(A\,B\,C\,D\,E\,F\,G\,H)$ ના કેન્દ્ર પર $q$ વિદ્યુતભાર મૂકવામાં આવે છે. કેન્દ્ર $O$ થી $L$ અંતરે $q$ વિદ્યુતભાર મૂકવામાં આવે છે. $BGFC$ માંથી પસાર થતું વિદ્યુતફ્લક્સ કેટલું હશે?View Solution
- 10View Solutionઈલેકટ્રોન અને પ્રોટોન સમાન વિદ્યુતક્ષેત્રમાં મૂકેલા છે. તેઓના પ્રવેગનો ગુણોત્તર ...... છે.