$A$ ક્ષેત્રફળ ધરાવતા પાત્રમાં પાણી $3\,m$ ઊંચાઈ સુધી પાણી ભરેલ છે.તળીયેથી $52.5\, cm$ ઊંચાઈએ પાત્રની દીવાલમાં $‘A_0’$ ક્ષેત્રફળ ધરાવતું કાણું પાડવામાં આવે છે.જો $A_0/A = 0.1$ હોય તો $v^2$ ........ $m^2/s^2$ થાય. (જ્યાં $v$ એ કાણાંમાથી બહાર આવતા પાણીનો વેગ છે)
AIIMS 2008,AIIMS 2016, Medium
Download our app for free and get started
a
The square of the velocity of flux
The square of the velocity of flux
\({v^2} = \frac{{2gh}}{{1 - {{\left( {\frac{{{A_0}}}{A}} \right)}^2}}}\)
\( = \frac{{2 \times 10 \times 2.475}}{{1 - {{\left( {0.1} \right)}^2}}} = 50{m^2}/{s^2}\)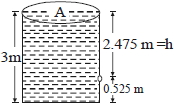
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$H$ ઊંચાઈ અને $\rho$ ઘનતા ધરાવતા ટેન્કમાં પ્રવાહી ભરવામાં આવે છે. તો આ કન્ટેનરની દીવાલ પર લાગતું સરેરાશ દબાણ.View Solution
- 2સોનાના ટુકડાનું હવામાં વજન $10 \,g$ અને $9 \,g$ પાણીમાં છે તો પોલાણ (cavity) નું કદ ........ $cc$ છે. (સોનાની ઘનતા = $\left.19.3 \,g cm ^{-3}\right)$View Solution
- 3કેશનળીને પાત્રના તળિયે જોડેલ છે,જો તેની ત્રિજયા $10\%$ વધારતાં પ્રવાહીના વહનમાં કેટલા $\%$ ફેરફાર થાય?View Solution
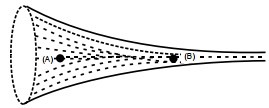
- 4આકૃતિમાં દર્શાવ્યા મુજબ બદલાતા જતા આડછેદના ક્ષેત્રફળવાળી નળીમાંથી આપેલ ધનતા ધરાવતું પ્રવાહી વહન પામે છે. જો $A$ આડછેદનું ક્ષેત્રફળ $1.5\,cm ^2$ અને $B$ નું $25\,mm ^2$ તથા જો $B$ આગળ પ્રવાહીની ઝડપ $60\,cm / s$ હોય. $\left( P _{ A }- P _{ B }\right)$ ............. $pa$ થશે. ($A$ અને $B$ બિંદુઓ આગળ પ્રવાહીના દબાણ $P_A$ અને $P_B$ છે. $\rho=1000\,kg\,m ^{-3}$ $A, B$, નળીની અક્ષ પરના બિંદુઓ છે.)View Solution
- 5પાત્રના તળિયે સમાન લંબાઇ ધરાવતી $r_1$ અને $ r_2$ ત્રિજયાવાળી કેશનળી જોડેલ છે.તો કેટલી ત્રિજયાની કેશનળી જોડવાથી પ્રવાહ અચળ રહે?View Solution
- 6$V$ કદનું પ્રવાહી મિશ્રાણ એ $\alpha$ અને $\beta$ ઘનતાઓ સાથેના બે પ્રવાહીઓ ધરાવે છે. જો મિશ્રણની ઘનતા $\sigma$ છે તો આ મિશ્રણમાં પહેલા પ્રવાહીનું દળ .......View Solution
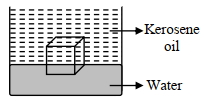
- 7એક બરફનો ચોસલો આંશિંક પાણીમાં અને આંશિક કેરોસીન તેલમાં તરે છે. પાણીમાં ડૂબાડેલ બરફના કદ અને કેરોસીન તેલમાંના બરફના કદનો ગુણોતર. . . . . . .છે (કેરોસીન તેલનુ) વિશિષ્ટ ગુરુત્વ = $0.8$ , બરફનું વિશિષ્ટ ગુરુત્વ =$0.9$) :View Solution
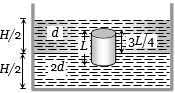
- 8આકૃતિમાં દર્શાવ્યા મુજબ પાત્રમાં $\frac{H}{2}$ ઊંચાઇ સુઘી $2d $ ઘનતાવાળું પ્રવાહી અને તેની ઉપરના ભાગમાં $\frac{H}{2}$ ઊંચાઇ સુઘી d ઘનતાવાળું પ્રવાહી ભરવામાં આવેલું છે.આ પાત્રમાં સમાન આડછેદના ક્ષેત્રફળ $\frac{A}{5}$ તથા $L$ લંબાઇ ( જયાં $L <$ $\frac{H}{2}$ ) ધરાવતો ઘન નળાકાર શિરોલંબ મૂકયો છે.હવે નળાકારના નીચેનો છેડો બંને પ્રવાહીને અલગ પાડતી સપાટીથી $\frac{L}{4}$ અંતરે રહે તેમ પ્રવાહીમાં શિરોલંબ તરે છે,તો નળાકારની ઘનતા $D = $ ________. ( ઉપરના પ્રવાહીની સપાટી પર વાતાવરણનું દબાણ $P_0$ છે.)View Solution
- 9એક બંધ નળી સાથે જોંડેલ દબાણ-મીટરમાં $4.5 \times 10^4 \mathrm{~N} / \mathrm{m}^2$ નું અવલોકન મળે છે. વાલ્વ ચાલુ કરતાં, પાણી વહેવાનું ચાલુ થાય છે અને દબાણ-મીટરમાં અવલોકન ઘટીને $2.0 \times 10^4 \mathrm{~N} / \mathrm{m}^2$ થાય છે. પાણીનો વેગ $\sqrt{\mathrm{V}} \mathrm{m} / \mathrm{s}$ માલૂમ પડે છે. $\mathrm{V}$ નું મૂલ્ય છે.View Solution
- 10પાણીનું એક નાનું બિંદુ $h$ ઊંચાઈએેથી સ્થિર અવસ્થામાંથી મુક્ત પતન કરે છે. તેનો અંતિમ વેગ એView Solution